|
Kleetope
In geometry and polyhedral combinatorics, the Kleetope of a polyhedron or higher-dimensional convex polytope is another polyhedron or polytope formed by replacing each facet of with a shallow pyramid. Kleetopes are named after Victor Klee. Examples The triakis tetrahedron is the Kleetope of a tetrahedron, the triakis octahedron is the Kleetope of an octahedron, and the triakis icosahedron is the Kleetope of an icosahedron. In each of these cases the Kleetope is formed by adding a triangular pyramid to each face of the original polyhedron. The tetrakis hexahedron is the Kleetope of the cube, formed by adding a square pyramid to each of its faces, and the pentakis dodecahedron is the Kleetope of the dodecahedron, formed by adding a pentagonal pyramid to each face of the dodecahedron. The base polyhedron of a Kleetope does not need to be a Platonic solid. For instance, the disdyakis dodecahedron is the Kleetope of the rhombic dodecahedron, formed by replacing each rhombus fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakisoctahedron
In geometry, a triakis octahedron (or trigonal trisoctahedron or kisoctahedronConway, Symmetries of things, p. 284) is an Archimedean solid, Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube. It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a ''trisoctahedron'', or, more fully, ''trigonal trisoctahedron''. Both names reflect that it has three triangular faces for every face of an octahedron. The ''tetragonal trisoctahedron'' is another name for the deltoidal icositetrahedron, a different polyhedron with three quadrilateral faces for every face of an octahedron. This convex polyhedron is topologically similar to the concave stellated octahedron. They have the same face connectivity, but the vertices are in different relative distances from the center. If its shorter edges have length 1, its surface area and volume are: :\begin A &= 3\sqrt \\ V &= \frac \e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakis Icosahedron
In geometry, the triakis icosahedron (or kisicosahedronConway, Symmetries of things, p.284) is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron. Cartesian coordinates Let \phi be the golden ratio. The 12 points given by (0, \pm 1, \pm \phi) and cyclic permutations of these coordinates are the vertices of a regular icosahedron. Its dual regular dodecahedron, whose edges intersect those of the icosahedron at right angles, has as vertices the points (\pm 1, \pm 1, \pm 1) together with the points (\pm\phi, \pm 1/\phi, 0) and cyclic permutations of these coordinates. Multiplying all coordinates of this dodecahedron by a factor of (7\phi-1)/11\approx 0.938\,748\,901\,93 gives a slightly smaller dodecahedron. The 20 vertices of this dodecahedron, together with the vertices of the icosahedron, are the vertices of a triakis icosahedron centered at the origin. The length of its long edges equals 2. Its faces are isosceles triangles with one obtuse angl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Victor Klee
Victor LaRue Klee, Jr. (September 18, 1925 – August 17, 2007) was a mathematician specialising in convex sets, functional analysis, analysis of algorithms, optimization, and combinatorics. He spent almost his entire career at the University of Washington in Seattle. Life Born in San Francisco, Vic Klee earned his B.A. degree in 1945 with high honors from Pomona College, majoring in mathematics and chemistry. He did his graduate studies, including a thesis on Convex Sets in Linear Spaces, and received his PhD in mathematics from the University of Virginia in 1949. After teaching for several years at the University of Virginia, he moved in 1953 to the University of Washington in Seattle, Washington, where he was a faculty member for 54 years. He died in Lakewood, Ohio. Research Klee wrote more than 240 research papers. He proposed Klee's measure problem and the art gallery problem. Kleetopes are also named after him, as is the Klee–Minty cube, which shows that the simpl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakis Octahedron
In geometry, a triakis octahedron (or trigonal trisoctahedron or kisoctahedronConway, Symmetries of things, p. 284) is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube. It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a ''trisoctahedron'', or, more fully, ''trigonal trisoctahedron''. Both names reflect that it has three triangular faces for every face of an octahedron. The ''tetragonal trisoctahedron'' is another name for the deltoidal icositetrahedron, a different polyhedron with three quadrilateral faces for every face of an octahedron. This convex polyhedron is topologically similar to the concave stellated octahedron. They have the same face connectivity, but the vertices are in different relative distances from the center. If its shorter edges have length 1, its surface area and volume are: :\begin A &= 3\sqrt \\ V &= \frac \end Cartesian coo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentakis Icosidodecahedron
In geometry, the pentakis icosidodecahedron or subdivided icosahedron is a convex polyhedron with 80 triangular faces, 120 edges, and 42 vertices. It is a dual of the ''truncated rhombic triacontahedron'' (chamfered dodecahedron). Construction Its name comes from a topological construction from the icosidodecahedron with the kis operator applied to the pentagonal faces. In this construction, all the vertices are assumed to be the same distance from the center, while in general icosahedral symmetry can be maintained even with the 12 order-5 vertices at a different distance from the center as the other 30. It can also be topologically constructed from the icosahedron, dividing each triangular face into 4 triangles by adding mid-edge vertices. From this construction, all 80 triangles will be equilateral, but faces will be coplanar. Related polyhedra File:Icosidodecahedron.png, Icosidodecahedron File:Pentakisdodecahedron.jpg, Pentakis dodecahedron is a slightly smaller Cat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentakis Dodecahedron
In geometry, a pentakis dodecahedron or kisdodecahedron is the polyhedron created by attaching a pentagonal pyramid to each face of a regular dodecahedron; that is, it is the Kleetope of the dodecahedron. It is a Catalan solid, meaning that it is a dual of an Archimedean solid, in this case, the truncated icosahedron. Cartesian coordinates Let \phi be the golden ratio. The 12 points given by (0, \pm 1, \pm \phi) and cyclic permutations of these coordinates are the vertices of a regular icosahedron. Its dual regular dodecahedron, whose edges intersect those of the icosahedron at right angles, has as vertices the points (\pm 1, \pm 1, \pm 1) together with the points (\pm\phi, \pm 1/\phi, 0) and cyclic permutations of these coordinates. Multiplying all coordinates of the icosahedron by a factor of (3\phi+12)/19\approx 0.887\,057\,998\,22 gives a slightly smaller icosahedron. The 12 vertices of this icosahedron, together with the vertices of the dodecahedron, are the vertices o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakistetrahedron
In geometry, a triakis tetrahedron (or kistetrahedron) is a Catalan solid with 12 faces. Each Catalan solid is the dual of an Archimedean solid. The dual of the triakis tetrahedron is the truncated tetrahedron. The triakis tetrahedron can be seen as a tetrahedron with a triangular pyramid added to each face; that is, it is the Kleetope of the tetrahedron. It is very similar to the net for the 5-cell, as the net for a tetrahedron is a triangle with other triangles added to each edge, the net for the 5-cell a tetrahedron with pyramids attached to each face. This interpretation is expressed in the name. The length of the shorter edges is that of the longer edges. If the triakis tetrahedron has shorter edge length 1, it has area and volume . Cartesian coordinates Cartesian coordinates for the 8 vertices of a triakis tetrahedron centered at the origin, are the points (±5/3, ±5/3, ±5/3) with an even number of minus signs, along with the points (±1, ±1, ±1) with an odd numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
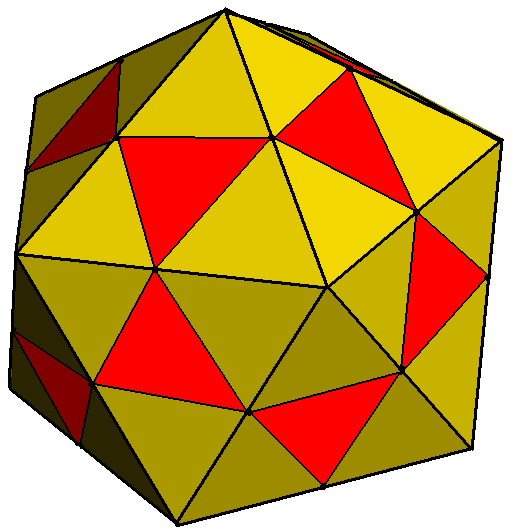
Disdyakisdodecahedron
In geometry, a disdyakis dodecahedron, (also hexoctahedron, hexakis octahedron, octakis cube, octakis hexahedron, kisrhombic dodecahedron), is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it. More formally, the disdyakis dodecahedron is the Kleetope of the rhombic dodecahedron, and the barycentric subdivision of the cube or of the regular octahedron. The net of the rhombic dodecahedral pyramid also shares the same topology. Symmetry It has Oh octahedral symmetry. Its collective edges represent the reflection planes of the symmetry. It can also be seen in the corner and mid-edge triangulation of the regular cube and octahedron, and rhombic dodecahedron. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disdyakis Dodecahedron
In geometry, a disdyakis dodecahedron, (also hexoctahedron, hexakis octahedron, octakis cube, octakis hexahedron, kisrhombic dodecahedron), is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it. More formally, the disdyakis dodecahedron is the Kleetope of the rhombic dodecahedron, and the barycentric subdivision of the cube or of the regular octahedron. The net of the rhombic dodecahedral pyramid also shares the same topology. Symmetry It has Oh octahedral symmetry. Its collective edges represent the reflection planes of the symmetry. It can also be seen in the corner and mid-edge triangulation of the regular cube and octahedron, and rhombic dodecahedron. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakis Tetrahedron
In geometry, a triakis tetrahedron (or kistetrahedron) is a Catalan solid with 12 faces. Each Catalan solid is the dual of an Archimedean solid. The dual of the triakis tetrahedron is the truncated tetrahedron. The triakis tetrahedron can be seen as a tetrahedron with a triangular pyramid added to each face; that is, it is the Kleetope of the tetrahedron. It is very similar to the net for the 5-cell, as the net for a tetrahedron is a triangle with other triangles added to each edge, the net for the 5-cell a tetrahedron with pyramids attached to each face. This interpretation is expressed in the name. The length of the shorter edges is that of the longer edges. If the triakis tetrahedron has shorter edge length 1, it has area and volume . Cartesian coordinates Cartesian coordinates for the 8 vertices of a triakis tetrahedron centered at the origin, are the points (±5/3, ±5/3, ±5/3) with an even number of minus signs, along with the points (±1, ±1, ±1) with an odd numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
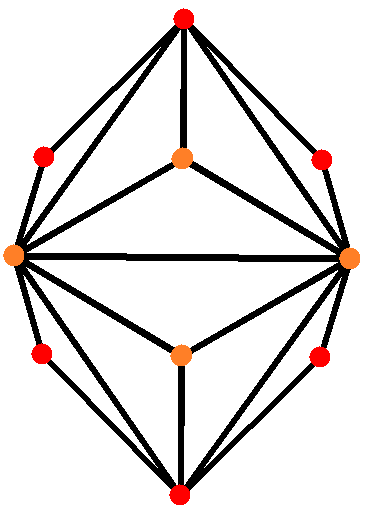
Rhombic Dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron. Properties The rhombic dodecahedron is a zonohedron. Its polyhedral dual is the cuboctahedron. The long face-diagonal length is exactly times the short face-diagonal length; thus, the acute angles on each face measure arccos(), or approximately 70.53°. Being the dual of an Archimedean polyhedron, the rhombic dodecahedron is face-transitive, meaning the symmetry group of the solid acts transitively on its set of faces. In elementary terms, this means that for any two faces A and B, there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B. The rhombic dodecahedron can be viewed as the convex hull of the union of the vertices of a cube and an octahedron. The 6 vertices where 4 rhombi meet correspond t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
