|
Instantaneous Phase
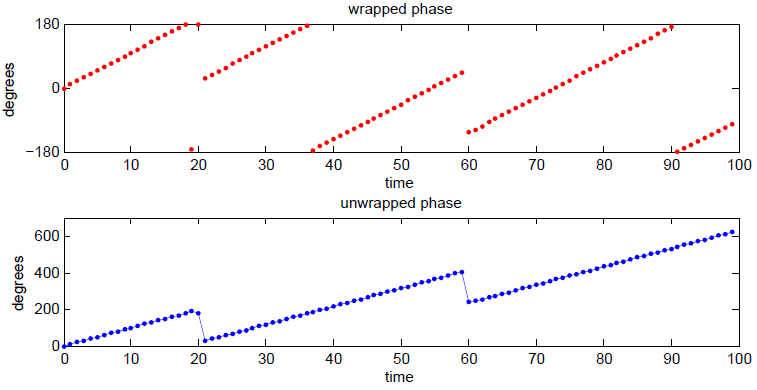
Instantaneous phase and frequency are important concepts in signal processing that occur in the context of the representation and analysis of time-varying functions. The instantaneous phase (also known as local phase or simply phase) of a ''complex-valued'' function ''s''(''t''), is the real-valued function: :\varphi(t) = \arg\, where arg is the complex argument function. The instantaneous frequency is the temporal rate of change of the instantaneous phase. And for a ''real-valued'' function ''s''(''t''), it is determined from the function's analytic representation, ''s''a(''t''): :\begin \varphi(t) &= \arg\ \\ pt &= \arg\, \end where \hat(t) represents the Hilbert transform of ''s''(''t''). When ''φ''(''t'') is constrained to its principal value, either the interval or , it is called ''wrapped phase''. Otherwise it is called ''unwrapped phase'', which is a continuous function of argument ''t'', assuming ''s''a(''t'') is a continuous function of ''t''. Unless ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, subjective video quality and to also detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was published in the Bell System Technical Journal. The paper laid the groundwork for later development of information c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
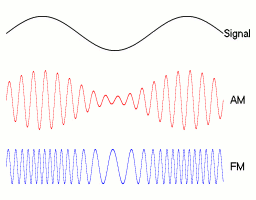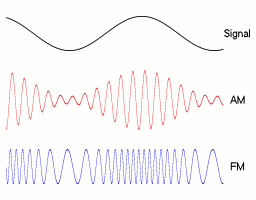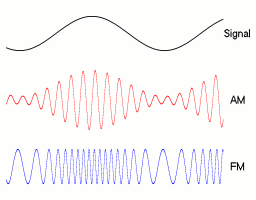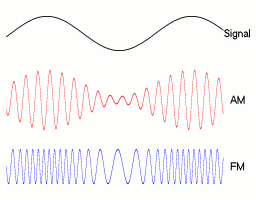
Frequency Modulation
Frequency modulation (FM) is the encoding of information in a carrier wave by varying the instantaneous frequency of the wave. The technology is used in telecommunications, radio broadcasting, signal processing, and Run-length limited#FM: .280.2C1.29 RLL, computing. In Analog signal, analog frequency modulation, such as radio broadcasting, of an audio signal representing voice or music, the instantaneous frequency deviation, i.e. the difference between the frequency of the carrier and its center frequency, has a functional relation to the modulating signal amplitude. Digital data can be encoded and transmitted with a type of frequency modulation known as frequency-shift keying (FSK), in which the instantaneous frequency of the carrier is shifted among a set of frequencies. The frequencies may represent digits, such as '0' and '1'. FSK is widely used in computer modems, such as fax modems, telephone caller ID systems, garage door openers, and other low-frequency transmissions. R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer. The subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term ''Fourier ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time–frequency Analysis
In signal processing, time–frequency analysis comprises those techniques that study a signal in both the time and frequency domains ''simultaneously,'' using various time–frequency representations. Rather than viewing a 1-dimensional signal (a function, real or complex-valued, whose domain is the real line) and some transform (another function whose domain is the real line, obtained from the original via some transform), time–frequency analysis studies a two-dimensional signal – a function whose domain is the two-dimensional real plane, obtained from the signal via a time–frequency transform. The mathematical motivation for this study is that functions and their transform representation are tightly connected, and they can be understood better by studying them jointly, as a two-dimensional object, rather than separately. A simple example is that the 4-fold periodicity of the Fourier transform – and the fact that two-fold Fourier transform reverses direction – can be int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Signal Processing
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are a sequence of numbers that represent samples of a continuous variable in a domain such as time, space, or frequency. In digital electronics, a digital signal is represented as a pulse train, which is typically generated by the switching of a transistor. Digital signal processing and analog signal processing are subfields of signal processing. DSP applications include audio and speech processing, sonar, radar and other sensor array processing, spectral density estimation, statistical signal processing, digital image processing, data compression, video coding, audio coding, image compression, signal processing for telecommunications, control systems, biomedical engineering, and seismology, among others. DSP can involve linear or nonli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, subjective video quality and to also detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was published in the Bell System Technical Journal. The paper laid the groundwork for later development of information c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negative Frequency
The concept of signed frequency (negative and positive frequency) can indicate both the rate and sense of rotation; it can be as simple as a wheel rotating clockwise or counterclockwise. The rate is expressed in units such as revolutions (a.k.a. ''cycles'') per second (hertz) or radian/second (where 1 cycle corresponds to 2''π'' radians). Sinusoids Let be a nonnegative angular frequency with units of radians/second. Then the function has slope , which is called a negative frequency. But when the function is used as the argument of a cosine operator, the result is indistinguishable from . Similarly, is indistinguishable from . Thus any sinusoid can be represented in terms of positive frequencies. The sign of the underlying phase slope is ambiguous. The ambiguity is resolved when the cosine and sine operators can be observed simultaneously, because leads by 1/4 cycle (= ''π''/2 radians) when , and lags by 1/4 cycle when . Similarly, a vector, , rotates counter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instantaneous Amplitude
In physics and engineering, the envelope of an oscillating signal is a smooth curve outlining its extremes. The envelope thus generalizes the concept of a constant amplitude into an instantaneous amplitude. The figure illustrates a modulated sine wave varying between an ''upper envelope'' and a ''lower envelope''. The envelope function may be a function of time, space, angle, or indeed of any variable. In beating waves A common situation resulting in an envelope function in both space ''x'' and time ''t'' is the superposition of two waves of almost the same wavelength and frequency: : \begin F(x, \ t) & = \sin \left 2 \pi \left( \frac - ( f + \Delta f )t \right) \right+ \sin \left 2 \pi \left( \frac - ( f - \Delta f )t \right) \right\\ pt& \approx 2\cos \left 2 \pi \left( \frac - \Delta f \ t \right) \right\ \sin \left 2 \pi \left( \frac - f \ t \right) \right\end which uses the trigonometric formula for the addition of two sine waves, and the approximation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Delay
In signal processing, group delay and phase delay are delay times experienced by a signal's various frequency components when the signal passes through a system that is linear time-invariant (LTI), such as a microphone, coaxial cable, amplifier, loudspeaker, telecommunications system or ethernet cable. These delays are generally frequency dependent. This means that different frequency components experience different delays, which cause distortion of the signal's waveform as it passes through the system. This distortion can cause problems such as poor fidelity in analog video and analog audio, or a high bit-error rate in a digital bit stream. For a modulation signal (passband signal), the information carried by the signal is carried exclusively in the wave envelope. Group delay therefore operates only with the frequency components derived from the envelope. Introduction The group delay and phase delay properties of a linear time-invariant (LTI) system are functions of frequency ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Signal
In mathematics and signal processing, an analytic signal is a complex-valued function that has no negative frequency components. The real and imaginary parts of an analytic signal are real-valued functions related to each other by the Hilbert transform. The analytic representation of a real-valued function is an ''analytic signal'', comprising the original function and its Hilbert transform. This representation facilitates many mathematical manipulations. The basic idea is that the negative frequency components of the Fourier transform (or spectrum) of a real-valued function are superfluous, due to the Hermitian symmetry of such a spectrum. These negative frequency components can be discarded with no loss of information, provided one is willing to deal with a complex-valued function instead. That makes certain attributes of the function more accessible and facilitates the derivation of modulation and demodulation techniques, such as single-sideband. As long as the manipul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Argument (complex Analysis)
In mathematics (particularly in complex analysis), the argument of a complex number ''z'', denoted arg(''z''), is the angle between the positive real axis and the line joining the origin and ''z'', represented as a point in the complex plane, shown as \varphi in Figure 1. It is a multi-valued function operating on the nonzero complex numbers. To define a single-valued function, the principal value of the argument (sometimes denoted Arg ''z'') is used. It is often chosen to be the unique value of the argument that lies within the interval . Definition An argument of the complex number , denoted , is defined in two equivalent ways: #Geometrically, in the complex plane, as the 2D polar angle \varphi from the positive real axis to the vector representing . The numeric value is given by the angle in radians, and is positive if measured counterclockwise. #Algebraically, as any real quantity \varphi such that z = r (\cos \varphi + i \sin \varphi) = r e^ for some positive real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.png)