|
Interval Propagation
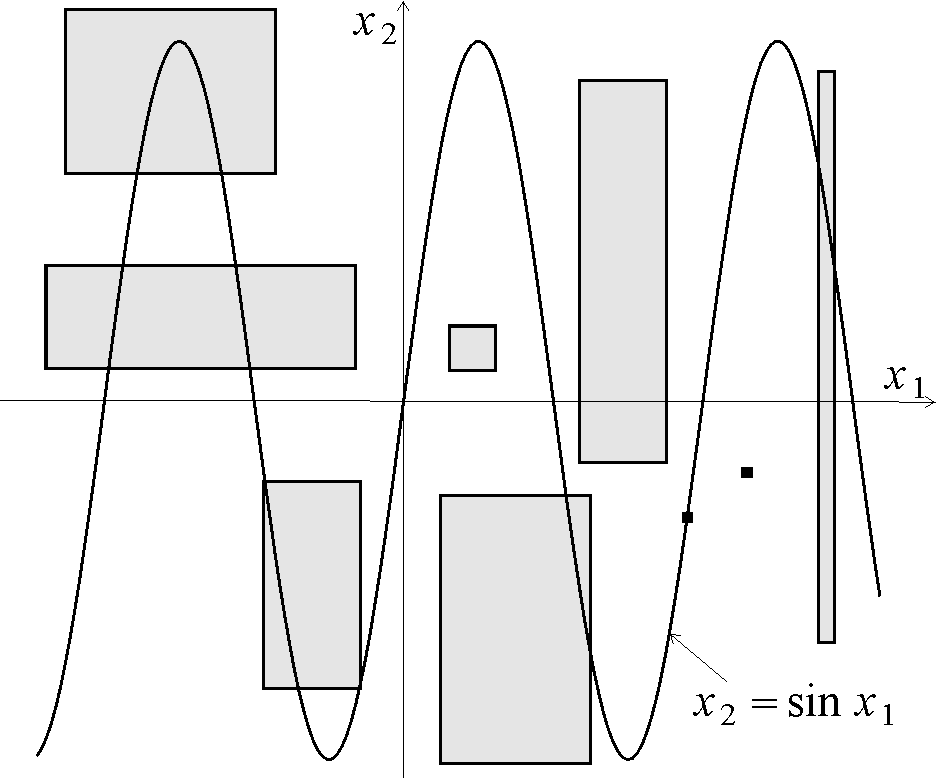
In numerical mathematics, interval propagation or interval constraint propagation is the problem of contracting interval domains associated to variables of R without removing any value that is consistent with a set of constraints (i.e., equations or inequalities). It can be used to propagate uncertainties in the situation where errors are represented by intervals. Interval propagation considers an estimation problem as a constraint satisfaction problem. Atomic contractors A contractor associated to an equation involving the variables ''x''1,...,''x''''n'' is an operator which contracts the intervals 'x''1..., 'x''''n''(that are supposed to enclose the ''x''''i'''s) without removing any value for the variables that is consistent with the equation. A contractor is said to be ''atomic'' if it is not built as a composition of other contractors. The main theory that is used to build atomic contractors are based on interval analysis. Example. Consider for instance the equation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Mathematics
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine and b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propagation Of Uncertainty
In statistics, propagation of uncertainty (or propagation of error) is the effect of variables' uncertainties (or errors, more specifically random errors) on the uncertainty of a function based on them. When the variables are the values of experimental measurements they have uncertainties due to measurement limitations (e.g., instrument precision) which propagate due to the combination of variables in the function. The uncertainty ''u'' can be expressed in a number of ways. It may be defined by the absolute error . Uncertainties can also be defined by the relative error , which is usually written as a percentage. Most commonly, the uncertainty on a quantity is quantified in terms of the standard deviation, , which is the positive square root of the variance. The value of a quantity and its error are then expressed as an interval . If the statistical probability distribution of the variable is known or can be assumed, it is possible to derive confidence limits to describ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Estimation
In statistics, a random vector ''x'' is classically represented by a probability density function. In a set-membership approach or set estimation, ''x'' is represented by a set ''X'' to which ''x'' is assumed to belong. This means that the support of the probability distribution function of ''x'' is included inside ''X''. On the one hand, representing random vectors by sets makes it possible to provide fewer assumptions on the random variables (such as independence) and dealing with nonlinearities is easier. On the other hand, a probability distribution function provides a more accurate information than a set enclosing its support. Set-membership estimation Set membership estimation (or ''set estimation'' for short) is an estimation approach which considers that measurements are represented by a set ''Y'' (most of the time a box of R''m'', where ''m'' is the number of measurements) of the measurement space. If ''p'' is the parameter vector and ''f'' is the model function, then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constraint Satisfaction
In artificial intelligence and operations research, constraint satisfaction is the process of finding a solution through a set of constraints that impose conditions that the variables must satisfy. A solution is therefore a set of values for the variables that satisfies all constraints—that is, a point in the feasible region. The techniques used in constraint satisfaction depend on the kind of constraints being considered. Often used are constraints on a finite domain, to the point that constraint satisfaction problems are typically identified with problems based on constraints on a finite domain. Such problems are usually solved via search, in particular a form of backtracking or local search. Constraint propagation are other methods used on such problems; most of them are incomplete in general, that is, they may solve the problem or prove it unsatisfiable, but not always. Constraint propagation methods are also used in conjunction with search to make a given proble ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval Arithmetic
Interval arithmetic (also known as interval mathematics, interval analysis, or interval computation) is a mathematical technique used to put bounds on rounding errors and measurement errors in mathematical computation. Numerical methods using interval arithmetic can guarantee reliable and mathematically correct results. Instead of representing a value as a single number, interval arithmetic represents each value as a range of possibilities. For example, instead of saying the height of someone is approximately 2 meters, one could using interval arithmetic, say that the height of the person is definitely between 1.97 meters and 2.03 meters. Mathematically, using interval arithmetic, instead of working with an uncertain real-valued variable x, one works with an interval ,b/math> that defines the range of values that x can have. In other words, any value of the variable x lies in the closed interval between a and b. A function f, when applied to x, yields an inexact value; f in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Before Contraction (BP), a timescale used mainly in geo ...
Before is the opposite of after, and may refer to: * ''Before'' (Gold Panda EP), 2009 * ''Before'' (James Blake EP), 2020 * "Before" (song), a 1996 song by the Pet Shop Boys * "Before", a song by the Empire of the Sun from ''Two Vines'' * "Before", a song by Anastacia from ''Evolution'' * "Before" (short story) by Gael Baudino * The Before film trilogy by Richard Linklater ** ''Before Sunrise'', 1995 ** ''Before Sunset'', 2004 ** ''Before Midnight'' (2013 film) See also *Before Christ (BC), an epoch used in dating years prior to the estimated birth of Jesus *Before Common Era (BCE), an alternative naming of the traditional calendar era primarily used in academic circles *Before Present Before Present (BP) years, or "years before present", is a time scale used mainly in archaeology, geology and other scientific disciplines to specify when events occurred relative to the origin of practical radiocarbon dating in the 1950s. Becaus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
After Contraction
After may refer to: Literature * ''After'' (Elgar), an 1895 poem by Philip Bourke Marston set to music by Edward Elgar * ''After'' (Prose novel), a 2003 novel by Francine Prose * ''After'' (book), a 2005 book by Canadian writer Francis Chalifour * ''After'' (Todd novel), a 2013 novel by Anna Todd *'' After: A Doctor Explores What Near-Death Experiences Reveal about Life and Beyond'', a 2021 book by Bruce Greyson Music * ''After'' (Ihsahn album), 2010 * ''After'' (Lady Lamb album), 2015 * ''After'' (Sammi Cheng album), 1995 * "After" (song), a 2011 song by Moby *(after), a 2018 live album by Mount Eerie *"After", a 2014 song by Amy Lee featuring Dave Eggar from the album ''Aftermath'' TV and film * After (2009 film), a Spanish drama film * ''After'' (2012 film), a sci-fi thriller film written and directed by Ryan Smith * ''After'', a 2012 film starring Julie Gayet * ''After'' (2019 film), an American film, based on the 2013 book * "After" (''The Handmaid's Tale''), a televi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval Contractor
In mathematics, an interval contractor (or contractor for short) associated to a set X is an operator C which associates to a hyperrectangle /math> in \bold^n another box C( of \bold^n such that the two following properties are always satisfied: * C( \subset /math> (contractance property) * C( \cap X = \cap X (completeness property) A ''contractor associated to a constraint'' (such as an equation or an inequality) is a contractor associated to the set X of all x which satisfy the constraint. Contractors make it possible to improve the efficiency of branch-and-bound algorithms classically used in interval analysis. Properties of contractors A contractor ''C'' is monotonic if we have \subset \Rightarrow C( \subset C( . It is ''minimal'' if for all boxes 'x'' we have C( = xcap X], where 'A''is the ''interval hull'' of the set ''A'', i.e., the smallest box enclosing ''A''. The contractor ''C'' is ''thin'' if for all points ''x'', C(\) = \\cap X where denot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronic Circuit To Illustrate The Interval Propagation
Electronic may refer to: *Electronics, the science of how to control electric energy in semiconductor * ''Electronics'' (magazine), a defunct American trade journal *Electronic storage, the storage of data using an electronic device *Electronic commerce or e-commerce, the trading in products or services using computer networks, such as the Internet * Electronic publishing or e-publishing, the digital publication of books and magazines using computer networks, such as the Internet *Electronic engineering, an electrical engineering discipline Entertainment *Electronic (band), an English alternative dance band ** ''Electronic'' (album), the self-titled debut album by British band Electronic *Electronic music, a music genre * Electronic musical instrument *Electronic game, a game that employs electronics See also *Electronica, an electronic music genre *Consumer electronics Consumer electronics or home electronics are Electronics, electronic (Analogue electronics, analog or digi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra Of Random Variables
The algebra of random variables in statistics, provides rules for the symbolic manipulation of random variables, while avoiding delving too deeply into the mathematically sophisticated ideas of probability theory. Its symbolism allows the treatment of sums, products, ratios and general functions of random variables, as well as dealing with operations such as finding the probability distributions and the expectations (or expected values), variances and covariances of such combinations. In principle, the elementary algebra of random variables is equivalent to that of conventional non-random (or deterministic) variables. However, the changes occurring on the probability distribution of a random variable obtained after performing algebraic operations are not straightforward. Therefore, the behavior of the different operators of the probability distribution, such as expected values, variances, covariances, and moments, may be different from that observed for the random variable us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |