|
Hidden Oscillation
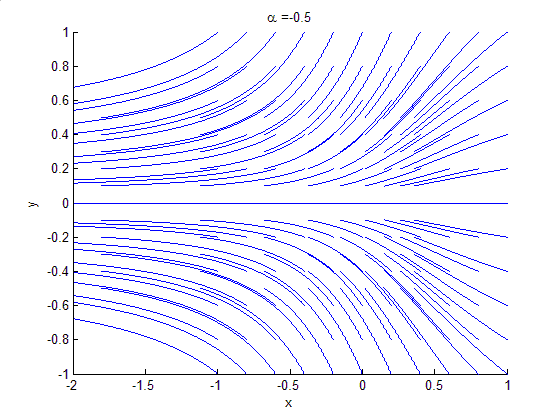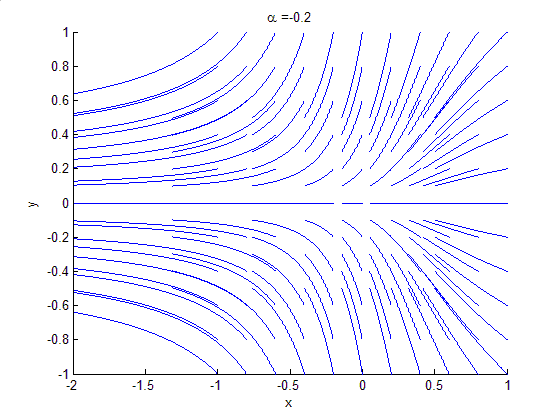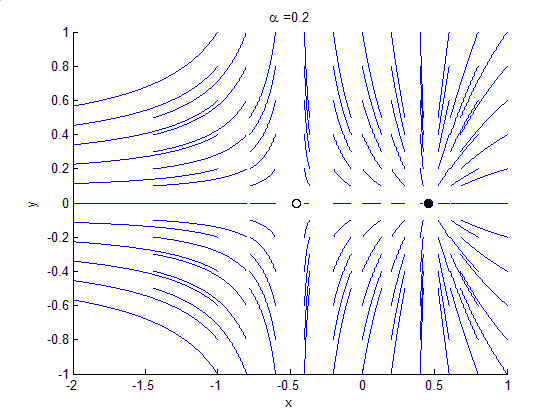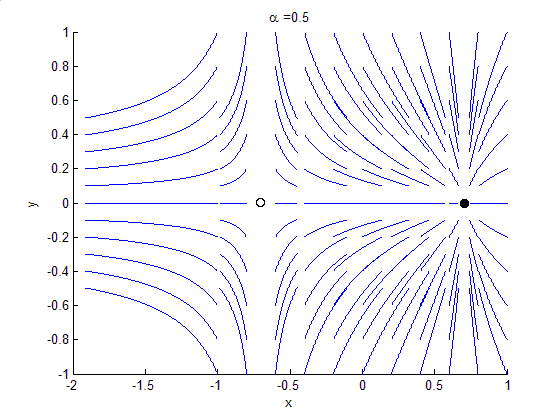
In the bifurcation theory, a bounded oscillation that is born without loss of stability of stationary set is called a hidden oscillation. In nonlinear control theory, the birth of a hidden oscillation in a time-invariant control system with bounded states means crossing a boundary, in the domain of the parameters, where local stability of the stationary states implies global stability (see, e.g. Kalman's conjecture). If a hidden oscillation (or a set of such hidden oscillations filling a compact subset of the phase space of the dynamical system) attracts all nearby oscillations, then it is called a hidden attractor. For a dynamical system with a unique equilibrium point that is globally attractive, the birth of a hidden attractor corresponds to a qualitative change in behaviour from monostability to bi-stability. In the general case, a dynamical system may turn out to be multistable and have coexisting local attractors in the phase space. While trivial attractors, i.e. stable equi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifurcation Theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by ordinary, delay or partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Henri Poincaré also later named various types of stationary points and classified them . Bifurcation types It is useful to divide bifurcations into two principal classes: * Local bifurcations, which can b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a deformation being called a homotopy (, ; , ) between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology. In practice, there are technical difficulties in using homotopies with certain spaces. Algebraic topologists work with compactly generated spaces, CW complexes, or spectra. Formal definition Formally, a homotopy between two continuous functions ''f'' and ''g'' from a topological space ''X'' to a topological space ''Y'' is defined to be a continuous function H: X \times ,1\to Y from the product of the space ''X'' with the unit interval , 1to ''Y'' such that H(x,0) = f(x) and H(x,1) = g(x) for all x \in X. If we think of the second ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aizerman's Conjecture
In nonlinear control, Aizerman's conjecture or Aizerman problem states that a linear system in feedback with a sector nonlinearity would be stable if the linear system is stable for any linear gain of the sector. This conjecture was proven false but led to the (valid) sufficient criteria on absolute stability. Mathematical statement of Aizerman's conjecture (Aizerman problem) ''Consider a system with one scalar nonlinearity'' : \frac=Px+qf(e),\quad e=r^*x \quad x\in\mathbb R^n, ''where P is a constant n×n-matrix, q, r are constant n-dimensional vectors, ∗ is an operation of transposition, f(e) is scalar function, and f(0)=0. Suppose that the nonlinearity f is sector bounded, meaning that for some real'' k_1 and k_2 with k_1 |
Sommerfeld Effect
In mechanics, Sommerfeld effect is a phenomenon arising from feedback in the energy exchange between vibrating systems: for example, when for the rocking table, under given conditions, energy transmitted to the motor resulted not in higher revolutions but in stronger vibrations of the table. It is named after Arnold Sommerfeld. In 1902, A. Sommerfeld analyzed the vibrations caused by a motor driving an unbalanced weight and wrote that "''This experiment corresponds roughly to the case in which a factory owner has a machine set on a poor foundation running at 30 horsepower. He achieves an effective level of just 1/3, however, because only 10 horsepower are doing useful work, while 20 horsepower are transferred to the foundational masonry''". First mathematical descriptions of Sommerfeld effect were suggested by I. Blekhman and V. Konenko. Hidden attractors in Sommerfeld effect In the theory of hidden oscillations, Sommerfeld effect is explained by the multistability and presence in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eden’s Conjecture
In the mathematics of dynamical systems, Eden's conjecture states that the supremum of the local Lyapunov dimensions on the global attractor is achieved on a stationary point or an unstable periodic orbit embedded into the attractor. The validity of the conjecture was proved for a number of well-known systems having global attractor (e.g. for the global attractors in the Lorenz system, complex Ginzburg–Landau equation). It is named after Alp Eden, who proposed it in 1987. Kuznetsov–Eden's conjecture For local attractors, a ''conjecture on the Lyapunov dimension of self-excited attractor'', refined by N. Kuznetsov, is stated that for a typical system, the Lyapunov dimension of a self-excited attractor does not exceed the Lyapunov dimension of one of the unstable equilibria, the unstable manifold of which intersects with the basin of attraction and visualizes the attractor. The conjecture is valid, e.g., for the classical self-excited Lorenz attractor; for the self-e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hénon Map
The Hénon map, sometimes called Hénon–Pomeau attractor/map, is a discrete-time dynamical system. It is one of the most studied examples of dynamical systems that exhibit chaotic behavior. The Hénon map takes a point (''xn'', ''yn'') in the plane and maps it to a new point :\beginx_ = 1 - a x_n^2 + y_n\\y_ = b x_n.\end The map depends on two parameters, ''a'' and ''b'', which for the classical Hénon map have values of ''a'' = 1.4 and ''b'' = 0.3. For the classical values the Hénon map is chaotic. For other values of ''a'' and ''b'' the map may be chaotic, intermittent, or converge to a periodic orbit. An overview of the type of behavior of the map at different parameter values may be obtained from its orbit diagram. The map was introduced by Michel Hénon as a simplified model of the Poincaré section of the Lorenz model. For the classical map, an initial point of the plane will either approach a set of points known as the Hénon strange ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rössler Attractor
The Rössler attractor is the attractor for the Rössler system, a system of three non-linear ordinary differential equations originally studied by Otto Rössler in the 1970s... These differential equations define a continuous-time dynamical system that exhibits chaotic dynamics associated with the fractal properties of the attractor.. Some properties of the Rössler system can be deduced via linear methods such as eigenvectors, but the main features of the system require non-linear methods such as Poincaré maps and bifurcation diagrams. The original Rössler paper states the Rössler attractor was intended to behave similarly to the Lorenz attractor, but also be easier to analyze qualitatively. An orbit within the attractor follows an outward spiral close to the x, y plane around an unstable fixed point. Once the graph spirals out enough, a second fixed point influences the graph, causing a rise and twist in the z-dimension. In the time domain, it becomes apparent that alt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |