|
Hexagram
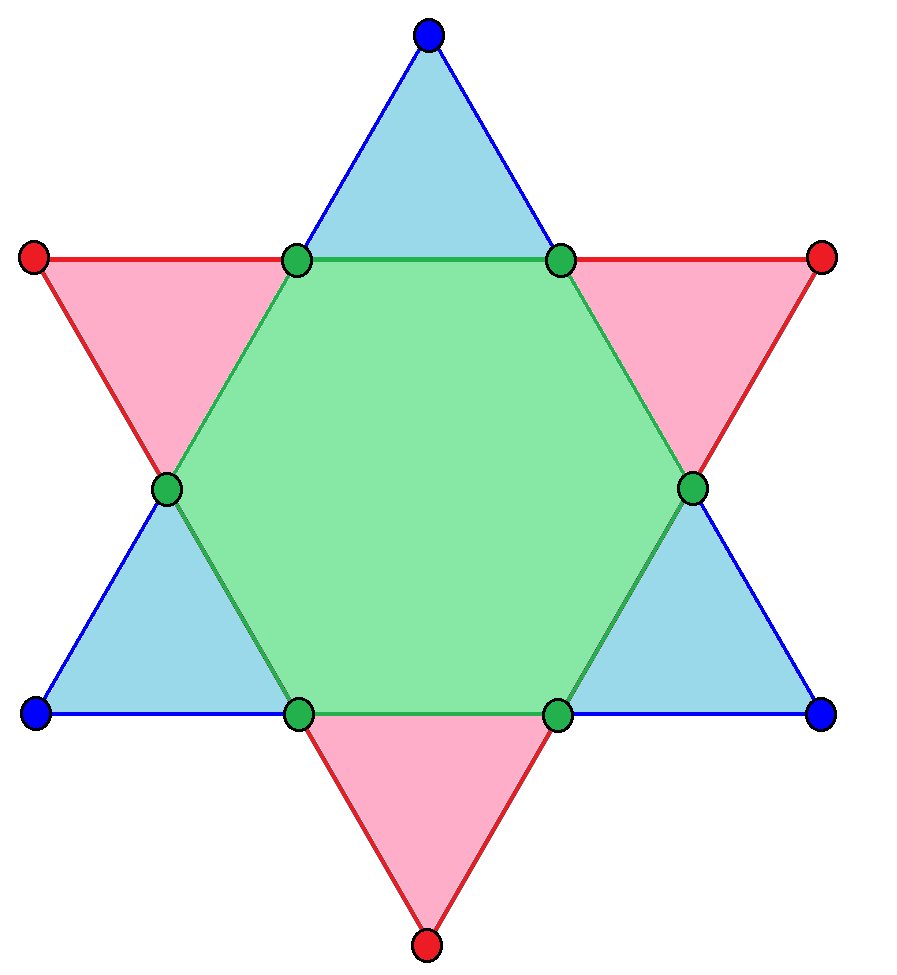
, can be seen as a compound composed of an upwards (blue here) and downwards (pink) facing equilateral triangle, with their intersection as a regular hexagon (in green). A hexagram ( Greek language, Greek) or sexagram (Latin) is a six-pointed geometric star figure with the Schläfli symbol , 2, or . Since there are no true regular continuous hexagrams, the term is instead used to refer to a compound figure of two equilateral triangles. The intersection is a regular hexagon. The hexagram is part of an infinite series of shapes which are compounds of two n-dimensional simplices. In three dimensions, the analogous compound is the stellated octahedron, and in four dimensions the compound of two 5-cells is obtained. It has been historically used in religious and cultural contexts and as decorative motifs. The symbol was used as a decorative motif in medieval Christian churches and Jewish synagogues. It was first used as a mystic symbol by Muslims in the medieval period, known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seal Of Solomon
The Seal of Solomon or Ring of Solomon ( he, חותם שלמה, '; ar, خاتم سليمان, ') is the legendary signet ring attributed to the Israelite king Solomon in medieval mystical traditions, from which it developed in parallel within Jewish mysticism, Islamic mysticism and Western occultism. It is the predecessor to the Star of David, the contemporary cultural and religious symbol of the Jewish people. It was often depicted in the shape of either a pentagram or a hexagram. In religious lore, the ring is variously described as having given Solomon the power to command the supernatural, including ' and ', and also the ability to speak with animals. Due to the proverbial wisdom of Solomon, it came to be seen as an amulet or talisman, or a symbol or character in medieval magic and Renaissance magic, occultism, and alchemy. Name The varied traditions refer to a seal, stamp or die, utilized to mark an impression often or most frequently by means of a signet ring ow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |