|
Hemi-icosahedron
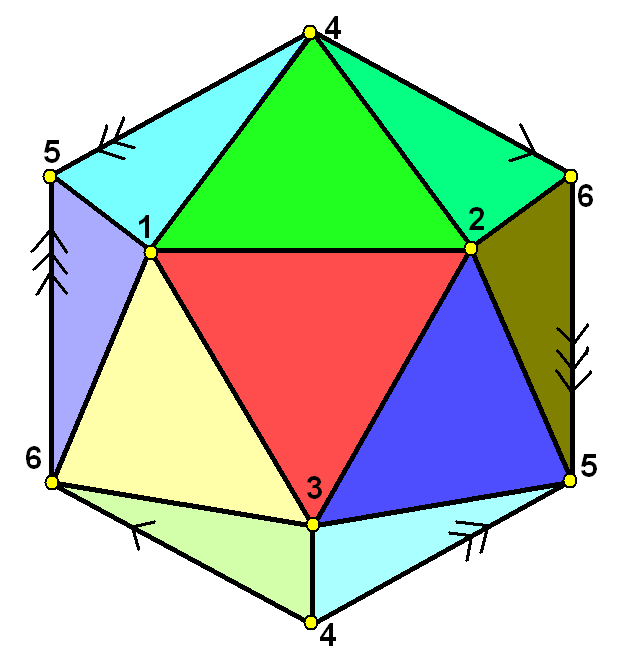
A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 10 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. Geometry It has 10 triangular faces, 15 edges, and 6 vertices. It is also related to the nonconvex uniform polyhedron, the tetrahemihexahedron, which could be topologically identical to the hemi-icosahedron if each of the 3 square faces were divided into two triangles. Graphs It can be represented symmetrically on faces, and vertices as Schlegel diagrams: The complete graph K6 It has the same vertices and edges as the 5-dimensional 5-simplex which has a complete graph of edges, but only contains half of the (20) faces. From the point of view of graph theory this is an embedding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemi-icosahedron
A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 10 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. Geometry It has 10 triangular faces, 15 edges, and 6 vertices. It is also related to the nonconvex uniform polyhedron, the tetrahemihexahedron, which could be topologically identical to the hemi-icosahedron if each of the 3 square faces were divided into two triangles. Graphs It can be represented symmetrically on faces, and vertices as Schlegel diagrams: The complete graph K6 It has the same vertices and edges as the 5-dimensional 5-simplex which has a complete graph of edges, but only contains half of the (20) faces. From the point of view of graph theory this is an embedding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
11-cell
In mathematics, the 11-cell (or hendecachoron) is a self-dual abstract regular 4-polytope ( four-dimensional polytope). Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. It has Schläfli symbol , with 3 hemi-icosahedra (Schläfli type ) around each edge. It has symmetry order 660, computed as the product of the number of cells (11) and the symmetry of each cell (60). The symmetry structure is the abstract group projective special linear group L2(11). It was discovered in 1977 by Branko Grünbaum, who constructed it by pasting hemi-icosahedra together, three at each edge, until the shape closed up. It was independently discovered by H. S. M. Coxeter in 1984, who studied its structure and symmetry in greater depth. Related polytopes Orthographic projection of 10-simplex with 11 vertices, 55 edges. The abstract ''11-cell'' contains the same number of vertices and edges as the 10-dimensional 10-simplex, and contains 1/3 of its 165 faces. Thus it can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemi-octahedron
A hemi-octahedron is an abstract regular polyhedron, containing half the faces of a regular octahedron. It has 4 triangular faces, 6 edges, and 3 vertices. Its dual polyhedron is the hemicube. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 4 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into four equal parts. It can be seen as a square pyramid without its base. It can be represented symmetrically as a hexagonal or square Schlegel diagram: : It has an unexpected property that there are two distinct edges between every pair of vertices – any two vertices define a digon. See also *Hemi-dodecahedron *Hemi-icosahedron A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real project ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Polyhedron
In geometry, a (globally) projective polyhedron is a tessellation of the real projective plane. These are projective analogs of spherical polyhedra – tessellations of the sphere – and toroidal polyhedra – tessellations of the toroids. Projective polyhedra are also referred to as elliptic tessellations or elliptic tilings, referring to the projective plane as (projective) elliptic geometry, by analogy with spherical tiling, a synonym for "spherical polyhedron". However, the term elliptic geometry applies to both spherical and projective geometries, so the term carries some ambiguity for polyhedra. As cellular decompositions of the projective plane, they have Euler characteristic 1, while spherical polyhedra have Euler characteristic 2. The qualifier "globally" is to contrast with ''locally'' projective polyhedra, which are defined in the theory of abstract polyhedra. Non-overlapping projective polyhedra (density 1) correspond to spherical polyhedra (equivalently, convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
4-polytope
In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces ( polygons), and cells ( polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853. The two-dimensional analogue of a 4-polytope is a polygon, and the three-dimensional analogue is a polyhedron. Topologically 4-polytopes are closely related to the uniform honeycombs, such as the cubic honeycomb, which tessellate 3-space; similarly the 3D cube is related to the infinite 2D square tiling. Convex 4-polytopes can be ''cut and unfolded'' as nets in 3-space. Definition A 4-polytope is a closed four-dimensional figure. It comprises vertices (corner points), edges, faces and cells. A cell is the three-dimensional analogue of a face, and is therefore a polyhedron. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Polytope
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines. A geometric polytope is said to be a ''realization'' of an abstract polytope in some real N-dimensional space, typically Euclidean. This abstract definition allows more general combinatorial structures than traditional definitions of a polytope, thus allowing new objects that have no counterpart in traditional theory. Introductory concepts Traditional versus abstract polytopes In Euclidean geometry, two shapes that are not similar can nonetheless share a common structure. For example a square and a trapezoid both comprise an alternating chain of four vertices and four sides, which makes them quadrilaterals. They are said to be isomorphic or “structure preserving”. This common structure may be represented in an underlying abstract polytope, a purely alg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Regular Polyhedron
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines. A geometric polytope is said to be a ''realization'' of an abstract polytope in some real N-dimensional space, typically Euclidean. This abstract definition allows more general combinatorial structures than traditional definitions of a polytope, thus allowing new objects that have no counterpart in traditional theory. Introductory concepts Traditional versus abstract polytopes In Euclidean geometry, two shapes that are not similar can nonetheless share a common structure. For example a square and a trapezoid both comprise an alternating chain of four vertices and four sides, which makes them quadrilaterals. They are said to be isomorphic or “structure preserving”. This common structure may be represented in an underlying abstract polytope, a purely algebr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemi-cube (geometry)
In abstract geometry, a hemicube is an abstract, regular polyhedron, containing half the faces of a cube. Realization It can be realized as a projective polyhedron (a tessellation of the real projective plane by three quadrilaterals), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. It has three square faces, six edges, and four vertices. It has an unexpected property that every face is in contact with every other face on two edges, and every face contains all the vertices, which gives an example of an abstract polytope whose faces are not determined by their vertex sets. From the point of view of graph theory the skeleton is a tetrahedral graph, an embedding of ''K''4 (the complete graph with four vertices) on a projective plane. The hemicube should not be confused with the demicube – the hemicube is a projective polyhedron, while the demic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Graph K6
Complete may refer to: Logic * Completeness (logic) * Completeness of a theory, the property of a theory that every formula in the theory's language or its negation is provable Mathematics * The completeness of the real numbers, which implies that there are no "holes" in the real numbers * Complete metric space, a metric space in which every Cauchy sequence converges * Complete uniform space, a uniform space where every Cauchy net in converges (or equivalently every Cauchy filter converges) * Complete measure, a measure space where every subset of every null set is measurable * Completion (algebra), at an ideal * Completeness (cryptography) * Completeness (statistics), a statistic that does not allow an unbiased estimator of zero * Complete graph, an undirected graph in which every pair of vertices has exactly one edge connecting them * Complete category, a category ''C'' where every diagram from a small category to ''C'' has a limit; it is ''cocomplete'' if every such functor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Petersen Graph
In the mathematics, mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertex (graph theory), vertices and 15 edge (graph theory), edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest Bridge (graph theory), bridgeless cubic graph with no three-edge-coloring. Although the graph is generally credited to Petersen, it had in fact first appeared 12 years earlier, in a paper by . Kempe observed that its vertices can represent the ten lines of the Desargues configuration, and its edges represent pairs of lines that do not meet at one of the ten points of the configuration. Donald Knuth states that the Petersen graph is "a remarkable configuration that serves as a counterexample to many optimistic predictions about what might be true for graphs in general." The Petersen graph also makes an appearanc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Graph
In the mathematical discipline of graph theory, the dual graph of a plane graph is a graph that has a vertex for each face of . The dual graph has an edge for each pair of faces in that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge of has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of . The definition of the dual depends on the choice of embedding of the graph , so it is a property of plane graphs (graphs that are already embedded in the plane) rather than planar graphs (graphs that may be embedded but for which the embedding is not yet known). For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph. Historically, the first form of graph duality to be recognized was the association of the Platonic solids into pairs of dual polyhedra. Graph duality is a topological ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges (one in each direction). Graph theory itself is typically dated as beginning with Leonhard Euler's 1736 work on the Seven Bridges of Königsberg. However, drawings of complete graphs, with their vertices placed on the points of a regular polygon, had already appeared in the 13th century, in the work of Ramon Llull. Such a drawing is sometimes referred to as a mystic rose. Properties The complete graph on vertices is denoted by . Some sources claim that the letter in this notation stands for the German word , but the German name for a complete graph, , does not contain the letter , and other sources state that the notation honors the contributions of Kazimierz Kuratowski to graph theory. has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |