|
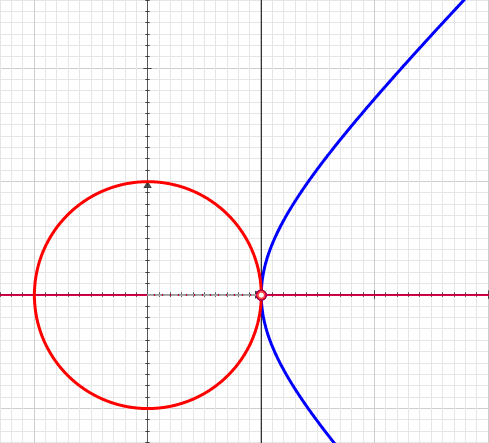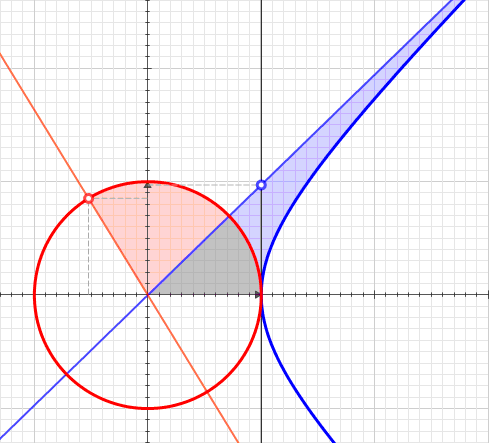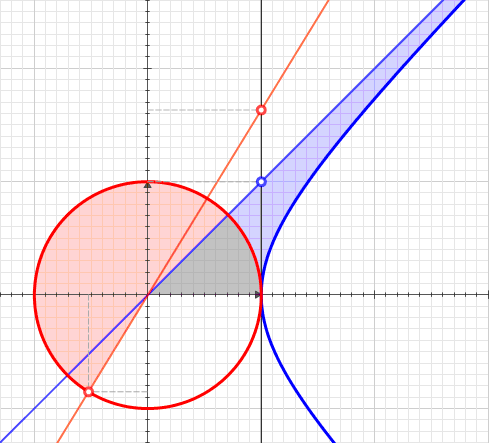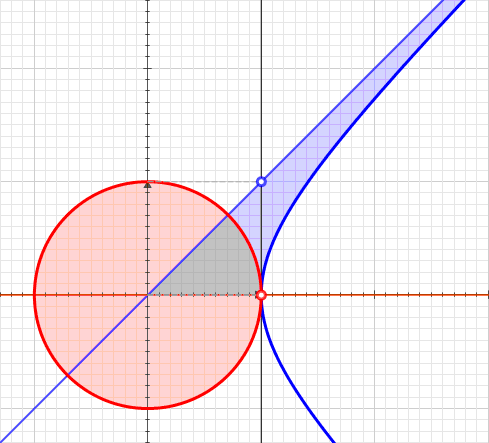
Harmonic Range
In mathematics, a projective range is a set of points in projective geometry considered in a unified fashion. A projective range may be a projective line or a conic. A projective range is the dual of a pencil of lines on a given point. For instance, a correlation interchanges the points of a projective range with the lines of a pencil. A projectivity is said to act from one range to another, though the two ranges may coincide as sets. A projective range expresses projective invariance of the relation of projective harmonic conjugates. Indeed, three points on a projective line determine a fourth by this relation. Application of a projectivity to this quadruple results in four points likewise in the harmonic relation. Such a quadruple of points is termed a harmonic range. In 1940 Julian Coolidge described this structure and identified its originator: :Two fundamental one-dimensional forms such as point ranges, pencils of lines, or of planes are defined as projective, when their membe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxford University Press
Oxford University Press (OUP) is the university press of the University of Oxford. It is the largest university press in the world, and its printing history dates back to the 1480s. Having been officially granted the legal right to print books by decree in 1586, it is the second oldest university press after Cambridge University Press. It is a department of the University of Oxford and is governed by a group of 15 academics known as the Delegates of the Press, who are appointed by the vice-chancellor of the University of Oxford. The Delegates of the Press are led by the Secretary to the Delegates, who serves as OUP's chief executive and as its major representative on other university bodies. Oxford University Press has had a similar governance structure since the 17th century. The press is located on Walton Street, Oxford, opposite Somerville College, in the inner suburb of Jericho. For the last 500 years, OUP has primarily focused on the publication of pedagogical texts and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Angle
In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of ''xy'' = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation. The hyperbola ''xy'' = 1 is rectangular with a semi-major axis of \sqrt 2, analogous to the magnitude of a circular angle corresponding to the area of a circular sector in a circle with radius \sqrt 2. Hyperbolic angle is used as the independent variable for the hyperbolic functions sinh, cosh, and tanh, because these functions may be premised on hyperbolic analogies to the corresponding circular trigonometric functions by regarding a hyperbolic angle as defining a hyperbolic triangle. The parameter thus becomes one of the most useful in the calculus of real variables. Definition Consider the rectangular hyperbola \text ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. Angles formed by two rays lie in the plane (geometry), plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection. ''Angle'' is also used to designate the measurement, measure of an angle or of a Rotation (mathematics), rotation. This measure is the ratio of the length of a arc (geometry), circular arc to its radius. In the case of a geometric angle, the arc is centered at the vertex and delimited by the sides. In the case of a rotation, the arc is centered at the center of the rotation and delimited by any other point and its image by the rotation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Hyperbolas arise in many ways: * as the curve representing the reciprocal function y(x) = 1/x in the Cartesian plane, * as the path followed by the shadow of the tip of a sundial, * as the shape of an open orbit (as distinct from a closed elliptical orbit), such as the orbit of a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with r=0 (a single point) is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. Specifically, a circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a '' disc''. A circle may also be defined as a special ki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, advocacy and other programs. The society is one of the four parts of the Joint Policy Board for Mathematics and a member of the Conference Board of the Mathematical Sciences. History The AMS was founded in 1888 as the New York Mathematical Society, the brainchild of Thomas Fiske, who was impressed by the London Mathematical Society on a visit to England. John Howard Van Amringe was the first president and Fiske became secretary. The society soon decided to publish a journal, but ran into some resistance, due to concerns about competing with the American Journal of Mathematics. The result was the ''Bulletin of the American Mathematical Society'', with Fiske as editor-in-chief. The de facto journal, as intended, was influential in in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karl Von Staudt
Karl Georg Christian von Staudt (24 January 1798 – 1 June 1867) was a German mathematician who used synthetic geometry to provide a foundation for arithmetic. Life and influence Karl was born in the Free Imperial City of Rothenburg, which is now called Rothenburg ob der Tauber in Germany. From 1814 he studied in Gymnasium in Ausbach. He attended the University of Göttingen from 1818 to 1822 where he studied with Gauss who was director of the observatory. Staudt provided an ephemeris for the orbits of Mars and the asteroid 2 Pallas, Pallas. When in 1821 Comet Nicollet-Pons was observed, he provided the elements of its orbit. These accomplishments in astronomy earned him his doctorate from University of Erlangen in 1822. Staudt's professional career began as a secondary school instructor in Würzburg until 1827 and then Nuremberg until 1835. He married Jeanette Dreschler in 1832. They had a son Eduard and daughter Mathilda, but Jeanette died in 1848. The book ''Geometrie der L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dover Publications
Dover Publications, also known as Dover Books, is an American book publisher founded in 1941 by Hayward and Blanche Cirker. It primarily reissues books that are out of print from their original publishers. These are often, but not always, books in the public domain. The original published editions may be scarce or historically significant. Dover republishes these books, making them available at a significantly reduced cost. Classic reprints Dover reprints classic works of literature, classical sheet music, and public-domain images from the 18th and 19th centuries. Dover also publishes an extensive collection of mathematical, scientific, and engineering texts. It often targets its reprints at a niche market, such as woodworking. Starting in 2015, the company branched out into graphic novel reprints, overseen by Dover acquisitions editor and former comics writer and editor Drew Ford. Most Dover reprints are photo facsimiles of the originals, retaining the original pagination and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Julian Coolidge
Julian Lowell Coolidge (September 28, 1873 – March 5, 1954) was an American mathematician, historian and a professor and chairman of the Harvard University Mathematics Department. Biography Born in Brookline, Massachusetts, he graduated from Harvard University and Oxford University. Between 1897 and 1899 Julian Coolidge taught at the Groton School where one of his students was Franklin D. Roosevelt. He left the private school to accept a teaching position at Harvard and in 1902 was given an assistant professorship, but took two years off to further his education with studies in Turin, Italy before receiving his doctorate from the University of Bonn. Julian Coolidge then returned to teach at Harvard where he remained for his entire academic career, interrupted only by a year at the Sorbonne in Paris as an exchange professor. During World War I, he served with the U.S. Army's Overseas Expeditionary Force in France, rising to the rank of major. In 1919, he was awarded a Knight of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points (called "points at infinity") to Euclidean points, and vice-versa. Properties meaningful for projective geometry are respected by this new idea of transformation, which is more radical in its effects than can be expressed by a transformation matrix and translations (the affine transformations). The first issue for geometers is what kind of geometry is adequate for a novel situation. It is not possible to refer to angles in projective geometry as it is in Euclidean geometry, because angle is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Harmonic Conjugate
In projective geometry, the harmonic conjugate point of an ordered triple of points on the real projective line is defined by the following construction: :Given three collinear points , let be a point not lying on their join and let any line through meet at respectively. If and meet at , and meets at , then is called the harmonic conjugate of with respect to . The point does not depend on what point is taken initially, nor upon what line through is used to find and . This fact follows from Desargues theorem. In real projective geometry, harmonic conjugacy can also be defined in terms of the cross-ratio as . Cross-ratio criterion The four points are sometimes called a harmonic range (on the real projective line) as it is found that always divides the segment ''internally'' in the same proportion as divides ''externally''. That is: :, AC, :, BC, = , AD, :, DB, \, . If these segments are now endowed with the ordinary metric interpretation of real num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)