|
Hemi-cuboctahedron
A hemi-cuboctahedron is an abstract polyhedron, containing half the faces of a semiregular cuboctahedron. It has 4 triangular faces and 3 square faces, 12 edges, and 6 vertices. It can be seen as a rectified hemi-octahedron or rectified hemi-cube. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 4 triangles and 3 square), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected. Dual Its dual polyhedron is a rhombic hemi-dodecahedron which has 7 vertices (1-7), 12 edges (a-l), and 6 rhombic faces (A-F). : Related polyhedra It has a real presentation as a uniform star polyhedron, the tetrahemihexahedron. : See also *Hemi-dodecahedron *Hemi-icosahedron A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 10 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahemihexahedron
In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 7 faces (4 triangles and 3 squares), 12 edges, and 6 vertices. Its vertex figure is a crossed quadrilateral. Its Coxeter–Dynkin diagram is (although this is a double covering of the tetrahemihexahedron). It is the only non-prismatic uniform polyhedron with an odd number of faces. Its Wythoff symbol is 3/2 3 , 2, but that represents a double covering of the tetrahemihexahedron with eight triangles and six squares, paired and coinciding in space. (It can more intuitively be seen as two coinciding tetrahemihexahedra.) It is a hemipolyhedron. The "hemi" part of the name means some of the faces form a group with half as many members as some regular polyhedron—here, three square faces form a group with half as many faces as the regular hexahedron, better known as the cube—hence ''hemihexahedron''. Hemi faces are also oriented in the same direction as the regular polyhe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Hemi-dodecahedron
A hemi-cuboctahedron is an abstract polyhedron, containing half the faces of a semiregular cuboctahedron. It has 4 triangular faces and 3 square faces, 12 edges, and 6 vertices. It can be seen as a rectified hemi-octahedron or rectified hemi-cube. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 4 triangles and 3 square), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected. Dual Its dual polyhedron is a rhombic hemi-dodecahedron which has 7 vertices (1-7), 12 edges (a-l), and 6 rhombic faces (A-F). : Related polyhedra It has a real presentation as a uniform star polyhedron, the tetrahemihexahedron In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 7 faces (4 triangles and 3 squares), 12 edges, and 6 vertices. Its vertex figure is a crossed quadrilateral. Its Coxeter–Dynkin dia .... : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schlegel Diagram
In geometry, a Schlegel diagram is a projection of a polytope from \mathbb^d into \mathbb^ through a point just outside one of its facets. The resulting entity is a polytopal subdivision of the facet in \mathbb^ that, together with the original facet, is combinatorially equivalent to the original polytope. The diagram is named for Victor Schlegel, who in 1886 introduced this tool for studying combinatorial and topological properties of polytopes. In dimension 3, a Schlegel diagram is a projection of a polyhedron into a plane figure; in dimension 4, it is a projection of a 4-polytope to 3-space. As such, Schlegel diagrams are commonly used as a means of visualizing four-dimensional polytopes. Construction The most elementary Schlegel diagram, that of a polyhedron, was described by Duncan Sommerville as follows: :A very useful method of representing a convex polyhedron is by plane projection. If it is projected from any external point, since each ray cuts it twice, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemicube (geometry)
In abstract geometry, a hemicube is an abstract, regular polyhedron, containing half the faces of a cube. Realization It can be realized as a projective polyhedron (a tessellation of the real projective plane by three quadrilaterals), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. It has three square faces, six edges, and four vertices. It has an unexpected property that every face is in contact with every other face on two edges, and every face contains all the vertices, which gives an example of an abstract polytope whose faces are not determined by their vertex sets. From the point of view of graph theory the skeleton is a tetrahedral graph, an embedding of ''K''4 (the complete graph with four vertices) on a projective plane. The hemicube should not be confused with the demicube – the hemicube is a projective polyhedron, while the de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
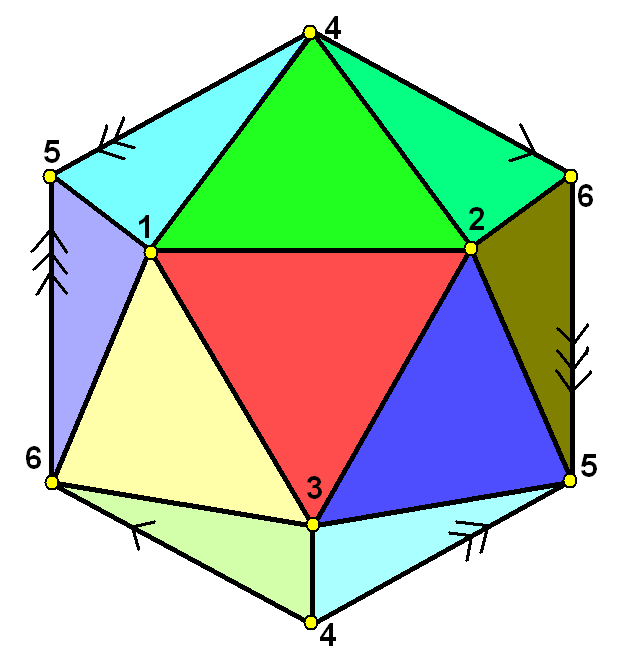
Hemi-icosahedron
A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 10 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. Geometry It has 10 triangular faces, 15 edges, and 6 vertices. It is also related to the nonconvex uniform polyhedron, the tetrahemihexahedron, which could be topologically identical to the hemi-icosahedron if each of the 3 square faces were divided into two triangles. Graphs It can be represented symmetrically on faces, and vertices as Schlegel diagrams: The complete graph K6 It has the same vertices and edges as the 5-dimensional 5-simplex which has a complete graph of edges, but only contains half of the (20) faces. From the point of view of graph theory this is an embedding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemi-dodecahedron
A hemi-dodecahedron is an abstract regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 6 pentagons), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. It has 6 pentagonal faces, 15 edges, and 10 vertices. Projections It can be projected symmetrically inside of a 10-sided or 12-sided perimeter: : Petersen graph From the point of view of graph theory this is an embedding of the Petersen graph on a real projective plane. With this embedding, the dual graph is ''K''6 (the complete graph with 6 vertices) --- see hemi-icosahedron. See also *57-cell – an abstract regular 4-polytope constructed from 57 hemi-dodecahedra. *hemi-icosahedron A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Star Polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both. The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedra, 5 quasiregular ones, and 48 semiregular ones. There are also two infinite sets of ''uniform star prisms'' and ''uniform star antiprisms''. Just as (nondegenerate) star polygons (which have polygon density greater than 1) correspond to circular polygons with overlapping tiles, star polyhedra that do not pass through the center have polytope density greater than 1, and correspond to spherical polyhedra with overlapping tiles; there are 47 nonprismatic such uniform star polyhedra. The remaining 10 nonprismatic uniform star polyhedra, those that pass through the center, are the hemipolyhedra as we ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral polyhedron (one in which any two faces are equivalent .., and vice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Projective Plane
In mathematics, the real projective plane is an example of a compact non- orientable two-dimensional manifold; in other words, a one-sided surface. It cannot be embedded in standard three-dimensional space without intersecting itself. It has basic applications to geometry, since the common construction of the real projective plane is as the space of lines in passing through the origin. The plane is also often described topologically, in terms of a construction based on the Möbius strip: if one could glue the (single) edge of the Möbius strip to itself in the correct direction, one would obtain the projective plane. (This cannot be done in three-dimensional space without the surface intersecting itself.) Equivalently, gluing a disk along the boundary of the Möbius strip gives the projective plane. Topologically, it has Euler characteristic 1, hence a demigenus (non-orientable genus, Euler genus) of 1. Since the Möbius strip, in turn, can be constructed from a square by g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries. A periodic tiling has a repeating pattern. Some special kinds include ''regular tilings'' with regular polygonal tiles all of the same shape, and ''semiregular tilings'' with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called "non-periodic". An ''aperiodic tiling'' uses a small set of tile shapes that cannot form a repeating pattern. A ''tessellation of space'', also known as a space filling or honeycomb, can be defined in the geometry of higher dimensions. A real physical tessellation is a tiling made of materials such as cemented ceramic squares or hexagons. Such t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemi-octahedron
A hemi-octahedron is an abstract regular polyhedron, containing half the faces of a regular octahedron. It has 4 triangular faces, 6 edges, and 3 vertices. Its dual polyhedron is the hemicube. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 4 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into four equal parts. It can be seen as a square pyramid without its base. It can be represented symmetrically as a hexagonal or square Schlegel diagram: : It has an unexpected property that there are two distinct edges between every pair of vertices – any two vertices define a digon. See also *Hemi-dodecahedron *Hemi-icosahedron A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real project ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |