|
Half-integers
In mathematics, a half-integer is a number of the form :n + \tfrac, where n is an whole number. For example, :, , , 8.5 are all ''half-integers''. The name "half-integer" is perhaps misleading, as the set may be misunderstood to include numbers such as 1 (being half the integer 2). A name such as "integer-plus-half" may be more accurate, but even though not literally true, "half integer" is the conventional term. Half-integers occur frequently enough in mathematics and in quantum mechanics that a distinct term is convenient. Note that halving an integer does not always produce a half-integer; this is only true for odd integers. For this reason, half-integers are also sometimes called half-odd-integers. Half-integers are a subset of the dyadic rationals (numbers produced by dividing an integer by a power of two). Notation and algebraic structure The set of all half-integers is often denoted :\mathbb Z + \tfrac \quad = \quad \left( \tfrac \mathbb Z \right) \smallsetminus \mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
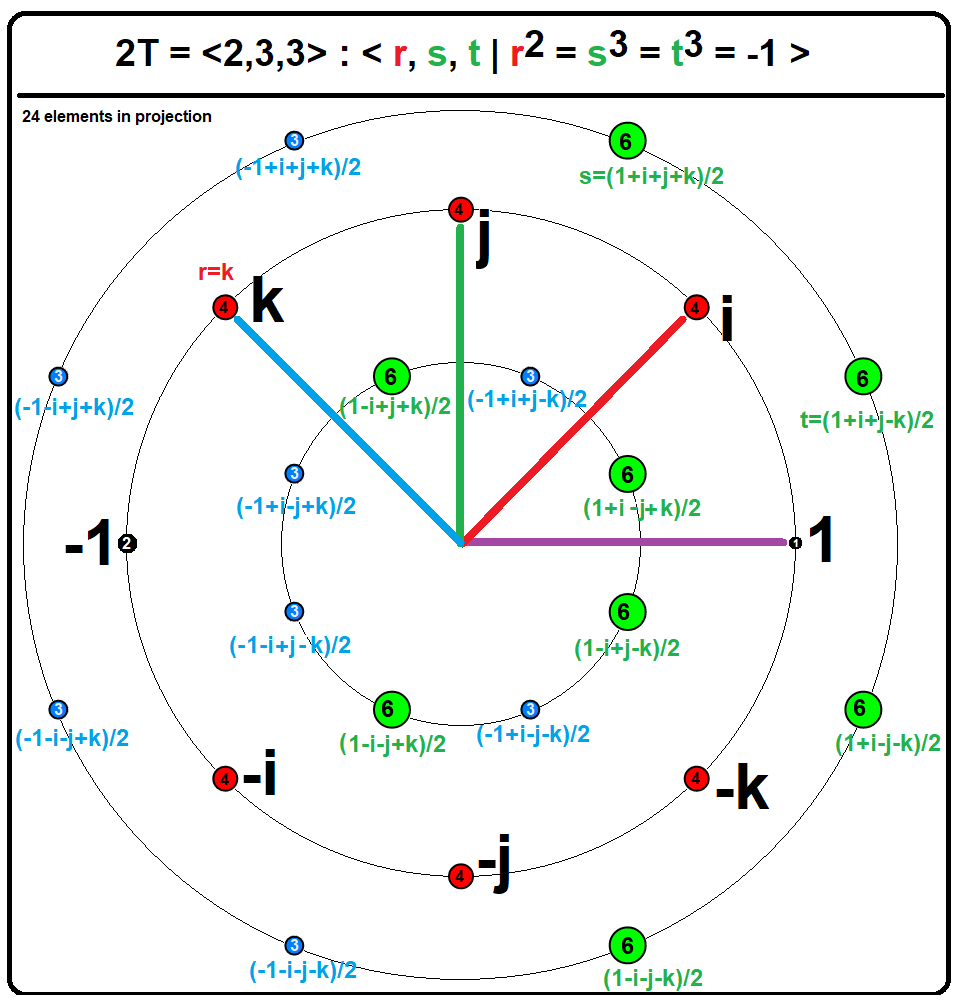
Hurwitz Integer
In mathematics, a Hurwitz quaternion (or Hurwitz integer) is a quaternion whose components are ''either'' all integers ''or'' all half-integers (halves of odd integers; a mixture of integers and half-integers is excluded). The set of all Hurwitz quaternions is :H = \left\. That is, either ''a'', ''b'', ''c'', ''d'' are all integers, or they are all half-integers. ''H'' is closed under quaternion multiplication and addition, which makes it a subring of the ring of all quaternions H. Hurwitz quaternions were introduced by . A Lipschitz quaternion (or Lipschitz integer) is a quaternion whose components are all integers. The set of all Lipschitz quaternions :L = \left\ forms a subring of the Hurwitz quaternions ''H''. Hurwitz integers have the advantage over Lipschitz integers that it is possible to perform Euclidean division on them, obtaining a small remainder. Both the Hurwitz and Lipschitz quaternions are examples of noncommutative domains which are not division rings. Struct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin (physics)
Spin is a conserved quantity carried by elementary particles, and thus by composite particles (hadrons) and atomic nucleus, atomic nuclei. Spin is one of two types of angular momentum in quantum mechanics, the other being ''orbital angular momentum''. The orbital angular momentum operator is the quantum-mechanical counterpart to the classical angular momentum of orbital revolution and appears when there is periodic structure to its wavefunction as the angle varies. For photons, spin is the quantum-mechanical counterpart of the Polarization (waves), polarization of light; for electrons, the spin has no classical counterpart. The existence of electron spin angular momentum is inferred from experiments, such as the Stern–Gerlach experiment, in which silver atoms were observed to possess two possible discrete angular momenta despite having no orbital angular momentum. The existence of the electron spin can also be inferred theoretically from the spin–statistics theorem and from th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quaternion as the quotient of two '' directed lines'' in a three-dimensional space, or, equivalently, as the quotient of two vectors. Multiplication of quaternions is noncommutative. Quaternions are generally represented in the form :a + b\ \mathbf i + c\ \mathbf j +d\ \mathbf k where , and are real numbers; and , and are the ''basic quaternions''. Quaternions are used in pure mathematics, but also have practical uses in applied mathematics, particularly for calculations involving three-dimensional rotations, such as in three-dimensional computer graphics, computer vision, and crystallographic texture analysis. They can be used alongside other methods of rotation, such as Euler angles and rotation matrices, or as an alternative to them ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Numbers
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all rational numbers, also referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by boldface , or blackboard bold \mathbb. A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: ), or eventually begins to repeat the same finite sequence of digits over and over (example: ). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see ). A real number that is not rational is called irrational. Irrational numbers include , , , and . Since the set of rational numbers is countable, and the set of real numbers is uncountable, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Factorial
In mathematics, the double factorial or semifactorial of a number , denoted by , is the product of all the integers from 1 up to that have the same parity (odd or even) as . That is, :n!! = \prod_^ (n-2k) = n (n-2) (n-4) \cdots. For even , the double factorial is :n!! = \prod_^\frac (2k) = n(n-2)(n-4)\cdots 4\cdot 2 \,, and for odd it is :n!! = \prod_^\frac (2k-1) = n(n-2)(n-4)\cdots 3\cdot 1 \,. For example, . The zero double factorial as an empty product. The sequence of double factorials for even = starts as : 1, 2, 8, 48, 384, 3840, 46080, 645120,... The sequence of double factorials for odd = starts as : 1, 3, 15, 105, 945, 10395, 135135,... The term odd factorial is sometimes used for the double factorial of an odd number. History and usage In a 1902 paper, the physicist Arthur Schuster wrote: states that the double factorial was originally introduced in order to simplify the expression of certain trigonometric integrals that arise in the derivation of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
National Institute Of Standards And Technology
The National Institute of Standards and Technology (NIST) is an agency of the United States Department of Commerce whose mission is to promote American innovation and industrial competitiveness. NIST's activities are organized into physical science laboratory programs that include nanoscale science and technology, engineering, information technology, neutron research, material measurement, and physical measurement. From 1901 to 1988, the agency was named the National Bureau of Standards. History Background The Articles of Confederation, ratified by the colonies in 1781, provided: The United States in Congress assembled shall also have the sole and exclusive right and power of regulating the alloy and value of coin struck by their own authority, or by that of the respective states—fixing the standards of weights and measures throughout the United States. Article 1, section 8, of the Constitution of the United States, ratified in 1789, granted these powers to the new Congr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume Of An N-ball
In geometry, a ball is a region in a space comprising all points within a fixed distance, called the radius, from a given point; that is, it is the region enclosed by a sphere or hypersphere. An -ball is a ball in an -dimensional Euclidean space. The volume of a -ball is the Lebesgue measure of this ball, which generalizes to any dimension the usual volume of a ball in 3-dimensional space. The volume of a -ball of radius is R^nV_n, where V_n is the volume of the unit -ball, the -ball of radius . The real number V_n can be expressed via a two-dimension recurrence relation. Closed-form expressions involve the gamma, factorial, or double factorial function. The volume can also be expressed in terms of A_n, the area of the unit -sphere. Formulas The first volumes are as follows: Two-dimension recurrence relation As is proved below using a vector-calculus double integral in polar coordinates, the volume of an -ball of radius can be expressed recursively in terms o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by , the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer , \Gamma(n) = (n-1)!\,. Derived by Daniel Bernoulli, for complex numbers with a positive real part, the gamma function is defined via a convergent improper integral: \Gamma(z) = \int_0^\infty t^ e^\,dt, \ \qquad \Re(z) > 0\,. The gamma function then is defined as the analytic continuation of this integral function to a meromorphic function that is holomorphic in the whole complex plane except zero and the negative integers, where the function has simple poles. The gamma function has no zeroes, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential function: \Gamma(z) = \mathcal M \ (z ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial: \begin n! &= n \times (n-1) \times (n-2) \times (n-3) \times \cdots \times 3 \times 2 \times 1 \\ &= n\times(n-1)!\\ \end For example, 5! = 5\times 4! = 5 \times 4 \times 3 \times 2 \times 1 = 120. The value of 0! is 1, according to the convention for an empty product. Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book '' Sefer Yetzirah''. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of n distinct objects: there In mathematical analysis, factorials are used in power series for the exponential function an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Harmonic Oscillator
量子調和振動子 は、 古典調和振動子 の 量子力学 類似物です。任意の滑らかな ポテンシャル は通常、安定した 平衡点 の近くで 調和ポテンシャル として近似できるため、最も量子力学における重要なモデル系。さらに、これは正確な 解析解法が知られている数少ない量子力学系の1つである。 author=Griffiths, David J. , title=量子力学入門 , エディション=2nd , 出版社=プレンティス・ホール , 年=2004 , isbn=978-0-13-805326-0 , author-link=David Griffiths (物理学者) , URL アクセス = 登録 , url=https://archive.org/details/introductiontoel00grif_0 One-dimensional harmonic oscillator Hamiltonian and energy eigenstates 粒子の ハミルトニアン は次のとおりです。 \hat H = \frac + \frac k ^2 = \frac + \frac m \omega^2 ^2 \, , ここで、 は粒子の質量、 は力定数、\omega = \sqrt は ��動子の [角周波数 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Level
A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized. In chemistry and atomic physics, an electron shell, or principal energy level, may be thought of as the orbit of one or more electrons around an atom's nucleus. The closest shell to the nucleus is called the " shell" (also called "K shell"), followed by the " shell" (or "L shell"), then the " shell" (or "M shell"), and so on farther and farther from the nucleus. The shells correspond with the principal quan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermion
In particle physics, a fermion is a particle that follows Fermi–Dirac statistics. Generally, it has a half-odd-integer spin: spin , spin , etc. In addition, these particles obey the Pauli exclusion principle. Fermions include all quarks and leptons and all composite particles made of an odd number of these, such as all baryons and many atoms and nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. Some fermions are elementary particles (such as electrons), and some are composite particles (such as protons). For example, according to the spin-statistics theorem in relativistic quantum field theory, particles with integer spin are bosons. In contrast, particles with half-integer spin are fermions. In addition to the spin characteristic, fermions have another specific property: they possess conserved baryon or lepton quantum numbers. Therefore, what is usually referred to as the spin-statistics relation is, in fact, a spin statistics-quantum numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |