|
Geometry And Topology
In mathematics, geometry and topology is an umbrella term for the historically distinct disciplines of geometry and topology, as general frameworks allow both disciplines to be manipulated uniformly, most visibly in local to global theorems in Riemannian geometry, and results like the Gauss–Bonnet theorem and Chern–Weil theory. Sharp distinctions between geometry and topology can be drawn, however, as discussed below. It is also the title of a journal '' Geometry & Topology'' that covers these topics. Scope It is distinct from "geometric topology", which more narrowly involves applications of topology to geometry. It includes: * Differential geometry and topology * Geometric topology (including low-dimensional topology and surgery theory) It does not include such parts of algebraic topology as homotopy theory, but some areas of geometry and topology (such as surgery theory, particularly algebraic surgery theory) are heavily algebraic. Distinction between geometry a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Space
In mathematics, a metric space is a set together with a notion of '' distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different branches of mathematics. Many types of mathematical objects have a natural notion of distance a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hawaiian Earring
In mathematics, the Hawaiian earring \mathbb is the topological space defined by the union of circles in the Euclidean plane \R^2 with center \left(\tfrac,0\right) and radius \tfrac for n = 1, 2, 3, \ldots endowed with the subspace topology: :\mathbb=\bigcup_^\left\ The space \mathbb is homeomorphic to the one-point compactification of the union of a countable family of disjoint open intervals. The Hawaiian earring is a one-dimensional, compact, locally path-connected metrizable space. Although \mathbb is locally homeomorphic to \R at all non-origin points, \mathbb is not semi-locally simply connected at (0,0). Therefore, \mathbb does not have a simply connected covering space and is usually given as the simplest example of a space with this complication. The Hawaiian earring looks very similar to the wedge sum of countably infinitely many circles; that is, the rose with infinitely many petals, but these two spaces are not homeomorphic. The difference between their to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Group
In the mathematical field of algebraic topology, the fundamental group of a topological space is the group of the equivalence classes under homotopy of the loops contained in the space. It records information about the basic shape, or holes, of the topological space. The fundamental group is the first and simplest homotopy group. The fundamental group is a homotopy invariant—topological spaces that are homotopy equivalent (or the stronger case of homeomorphic) have isomorphic fundamental groups. The fundamental group of a topological space X is denoted by \pi_1(X). Intuition Start with a space (for example, a surface), and some point in it, and all the loops both starting and ending at this point— paths that start at this point, wander around and eventually return to the starting point. Two loops can be combined in an obvious way: travel along the first loop, then along the second. Two loops are considered equivalent if one can be deformed into the other without breaki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Totally Disconnected
In topology and related branches of mathematics, a totally disconnected space is a topological space that has only singletons as connected subsets. In every topological space, the singletons (and, when it is considered connected, the empty set) are connected; in a totally disconnected space, these are the ''only'' connected proper subsets. An important example of a totally disconnected space is the Cantor set, which is homeomorphic to the set of ''p''-adic integers. Another example, playing a key role in algebraic number theory, is the field of ''p''-adic numbers. Definition A topological space X is totally disconnected if the connected components in X are the one-point sets. Analogously, a topological space X is totally path-disconnected if all path-components in X are the one-point sets. Another closely related notion is that of a totally separated space, i.e. a space where quasicomponents are singletons. That is, a topological space X is totally separated space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a deformation being called a homotopy (, ; , ) between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology. In practice, there are technical difficulties in using homotopies with certain spaces. Algebraic topologists work with compactly generated spaces, CW complexes, or spectra. Formal definition Formally, a homotopy between two continuous functions ''f'' and ''g'' from a topological space ''X'' to a topological space ''Y'' is defined to be a continuous function H: X \times ,1\to Y from the product of the space ''X'' with the unit interval , 1to ''Y'' such that H(x,0) = f(x) and H(x,1) = g(x) for all x \in X. If we think of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
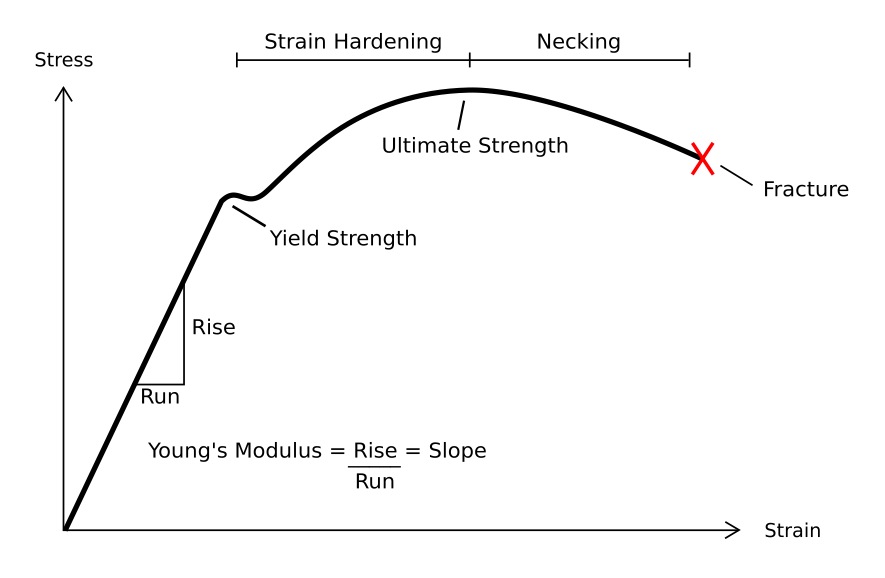
Deformation (engineering)
In engineering, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain is the ''relative'' internal change in shape of an infinitesimally small cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is elastic. The linear relationship for a material is known as Young's modulus. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials and for a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isometry
In mathematics, an isometry (or congruence, or congruent transformation) is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος ''isos'' meaning "equal", and μέτρον ''metron'' meaning "measure". Introduction Given a metric space (loosely, a set and a scheme for assigning distances between elements of the set), an isometry is a transformation which maps elements to the same or another metric space such that the distance between the image elements in the new metric space is equal to the distance between the elements in the original metric space. In a two-dimensional or three-dimensional Euclidean space, two geometric figures are congruent if they are related by an isometry; the isometry that relates them is either a rigid motion (translation or rotation), or a composition of a rigid motion and a reflection. Isometries are often used in constructions where one spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemannian Manifold
In differential geometry, a Riemannian manifold or Riemannian space , so called after the German mathematician Bernhard Riemann, is a real, smooth manifold ''M'' equipped with a positive-definite inner product ''g''''p'' on the tangent space ''T''''p''''M'' at each point ''p''. The family ''g''''p'' of inner products is called a Riemannian metric (or Riemannian metric tensor). Riemannian geometry is the study of Riemannian manifolds. A common convention is to take ''g'' to be smooth, which means that for any smooth coordinate chart on ''M'', the ''n''2 functions :g\left(\frac,\frac\right):U\to\mathbb are smooth functions. These functions are commonly designated as g_. With further restrictions on the g_, one could also consider Lipschitz Riemannian metrics or measurable Riemannian metrics, among many other possibilities. A Riemannian metric (tensor) makes it possible to define several geometric notions on a Riemannian manifold, such as angle at an intersection, le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curvature Of Riemannian Manifolds
In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension greater than 2 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define curvature for these manifolds, now known as the Riemann curvature tensor. Similar notions have found applications everywhere in differential geometry. For a more elementary discussion see the article on curvature which discusses the curvature of curves and surfaces in 2 and 3 dimensions, as well as the differential geometry of surfaces. The curvature of a pseudo-Riemannian manifold can be expressed in the same way with only slight modifications. Ways to express the curvature of a Riemannian manifold The Riemann curvature tensor The curvature of a Riemannian manifold can be described in various ways; the most standard one is the curvature tensor, given in terms of a Levi-Civita connection (or covariant differenti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as evident (for example, there is exactly one straight line passing through two points), or seemed impossible to prove (paral ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a vector space. To induce a global differential structure on the local coordinate systems induced by the homeomorphisms, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |