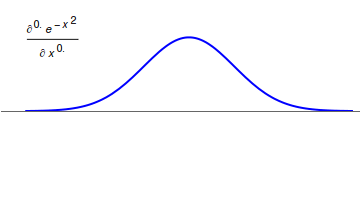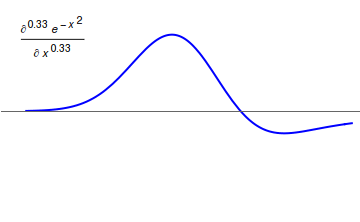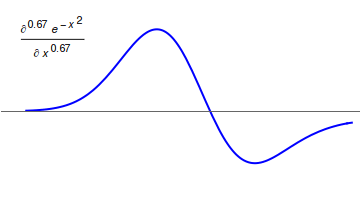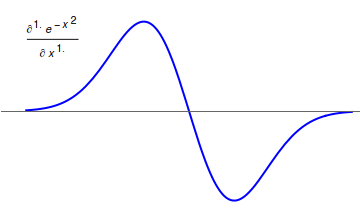
|
Fractional Integration
In fractional calculus, an area of mathematical analysis, the differintegral (sometime also called the derivigral) is a combined differentiation/ integration operator. Applied to a function ƒ, the ''q''-differintegral of ''f'', here denoted by :\mathbb^q f is the fractional derivative (if ''q'' > 0) or fractional integral (if ''q'' So, \frac = \mathcal^\left\ which generalizes to \mathbb^qf(t) = \mathcal^\left\. Under the bilateral Laplace transform, here denoted by \mathcal and defined as \mathcal (t)=\int_^\infty e^ f(t)\, dt, differentiation transforms into a multiplication \mathcal\left frac\right= s\mathcal (t) Generalizing to arbitrary order and solving for \mathbb^qf(t), one obtains \mathbb^qf(t)=\mathcal^\left\. Representation via Newton series is the Newton interpolation over consecutive integer orders: \mathbb^qf(t) =\sum_^ \binom m \sum_^m\binom mk(-1)^f^(x). For fractional derivative definitions described in this section, the following identities hold: :\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called aperiodic. Definition A function is said to be periodic if, for some nonzero constant , it is the case that :f(x+P) = f(x) for all values of in the domain. A nonzero constant for which this is the case is called a period of the function. If there exists a least positive constant with this property, it is called the fundamental period (also primitive period, basic period, or prime period.) Often, "the" period of a function is used to mean its fundamental period. A function with period will repeat on intervals of length , and these intervals are sometimes also referred to as periods of the function. Geometrically, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional-order Integrator
A fractional-order integrator or just simply fractional integrator is an integrator device that calculates the fractional-order integral or derivative (usually called a differintegral) of an input. Differentiation or integration is a real or complex parameter. The fractional integrator is useful in fractional-order control where the history of the system under control is important to the control system output. Overview The differintegral function, :_a \mathbb^q_t \left( f(x) \right) includes the integer order differentiation and integration functions, and allows a continuous range of functions around them. The differintegral parameters are ''a'', ''t'', and ''q''. The parameters ''a'' and ''t'' describe the range over which to compute the result. The differintegral parameter ''q'' may be any real number or complex number. If ''q'' is greater than zero, the differintegral computes a derivative. If ''q'' is less than zero, the differintegral computes an integral. The integer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative internal binary operation on it. The binary operation of a semigroup is most often denoted multiplicatively: ''x''·''y'', or simply ''xy'', denotes the result of applying the semigroup operation to the ordered pair . Associativity is formally expressed as that for all ''x'', ''y'' and ''z'' in the semigroup. Semigroups may be considered a special case of magmas, where the operation is associative, or as a generalization of groups, without requiring the existence of an identity element or inverses. The closure axiom is implied by the definition of a binary operation on a set. Some authors thus omit it and specify three axioms for a group and only one axiom (associativity) for a semigroup. As in the case of groups or magmas, the semigroup operation need not be commutative, so ''x''·''y'' is not necessarily equal to ''y''·''x''; a well-known example of an operation that is as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Operator
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a (linear) ''endomorphism''. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Sometimes the term ''linear function'' has the same meaning as ''linear map' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bilateral Laplace Transform
In mathematics, the two-sided Laplace transform or bilateral Laplace transform is an integral transform equivalent to probability's moment generating function. Two-sided Laplace transforms are closely related to the Fourier transform, the Mellin transform, the Z-transform and the ordinary or one-sided Laplace transform. If ''f''(''t'') is a real- or complex-valued function of the real variable ''t'' defined for all real numbers, then the two-sided Laplace transform is defined by the integral :\mathcal\(s) = F(s) = \int_^\infty e^ f(t)\, dt. The integral is most commonly understood as an improper integral, which converges if and only if both integrals :\int_0^\infty e^ f(t) \, dt,\quad \int_^0 e^ f(t)\, dt exist. There seems to be no generally accepted notation for the two-sided transform; the \mathcal used here recalls "bilateral". The two-sided transform used by some authors is :\mathcal\(s) = s\mathcal\(s) = sF(s) = s \int_^\infty e^ f(t)\, dt. In pure mathematics the argum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude (absolute value) of the complex value represents the amplitude of a constituent complex sinusoid with that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Caputo Differintegral
Caputo is a common Italian surname. It derives from the Latin root of ''caput'', meaning "source" or "head." People with that name include: * Anthony "Acid" Caputo, American DJ, producer and remixer * Bruce Faulkner Caputo, American politician * Chuck Caputo, American politician * Chuck Caputo, American magician * Dante Caputo, Argentine academic, politician and diplomat * David A. Caputo, American academic * Francesco Caputo, Italian footballer * John D. Caputo, American philosopher * John S. Caputo, American/Italian communication scholar * Joseph Claude Caputo, American jazz musician, known as Joe Cabot * Lisa Caputo, American businesswoman * Michael A. Caputo, American professional football player * Michael R. Caputo, Republican political strategist and media consultant * Michael "Mike" Caputo, American politician * Mina Caputo, formerly known as Keith Caputo, American singer * Philip Caputo, American writer * Sergio Caputo, Italian musician * Theresa Caputo, American ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weyl Differintegral
In mathematics, the Weyl integral (named after Hermann Weyl) is an operator defined, as an example of fractional calculus, on functions ''f'' on the unit circle having integral 0 and a Fourier series. In other words there is a Fourier series for ''f'' of the form : \sum_^ a_n e^ with ''a''0 = 0. Then the Weyl integral operator of order ''s'' is defined on Fourier series by : \sum_^ (in)^s a_n e^ where this is defined. Here ''s'' can take any real value, and for integer values ''k'' of ''s'' the series expansion is the expected ''k''-th derivative, if ''k'' > 0, or (−''k'')th indefinite integral normalized by integration from ''θ'' = 0. The condition ''a''0 = 0 here plays the obvious role of excluding the need to consider division by zero. The definition is due to Hermann Weyl Hermann Klaus Hugo Weyl, (; 9 November 1885 – 8 December 1955) was a German mathematician, theoretical physicist and philosopher. Although muc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (mathematics), series, and analytic functions. These theories are usually studied in the context of Real number, real and Complex number, complex numbers and Function (mathematics), functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any Space (mathematics), space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space). History Ancient Mathematical analysis formally developed in the 17th century during the Scientific Revolution, but many of its ideas can be traced back to earlier mathematicians. Early results in analysis were i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the derivativ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
