|
Fibrifold Notation
In mathematics, a fibrifold is (roughly) a fiber space whose fibers and base spaces are orbifolds. They were introduced by , who introduced a system of notation for 3-dimensional fibrifolds and used this to assign names to the 219 affine space group types. 184 of these are considered reducible, and 35 irreducible. Irreducible cubic space groups The 35 irreducible space groups correspond to the cubic space group. Irreducible group symbols (indexed 195−230) in Hermann–Mauguin notation, Fibrifold notation, geometric notation, and Coxeter notation In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram ...: References * * * * * Symmetry Finite groups Discrete groups {{geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fiber Space
In differential geometry, in the category of differentiable manifolds, a fibered manifold is a surjective submersion \pi : E \to B\, that is, a surjective differentiable mapping such that at each point y \in U the tangent mapping T_y \pi : T_ E \to T_B is surjective, or, equivalently, its rank equals \dim B. History In topology, the words fiber (Faser in German) and fiber space (gefaserter Raum) appeared for the first time in a paper by Herbert Seifert in 1932, but his definitions are limited to a very special case. The main difference from the present day conception of a fiber space, however, was that for Seifert what is now called the base space (topological space) of a fiber (topological) space E was not part of the structure, but derived from it as a quotient space of E. The first definition of fiber space is given by Hassler Whitney in 1935 under the name sphere space, but in 1940 Whitney changed the name to sphere bundle. The theory of fibered spaces, of which vector bun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbifold
In the mathematical disciplines of topology and geometry, an orbifold (for "orbit-manifold") is a generalization of a manifold. Roughly speaking, an orbifold is a topological space which is locally a finite group quotient of a Euclidean space. Definitions of orbifold have been given several times: by Ichirô Satake in the context of automorphic forms in the 1950s under the name ''V-manifold''; by William Thurston in the context of the geometry of 3-manifolds in the 1970s when he coined the name ''orbifold'', after a vote by his students; and by André Haefliger in the 1980s in the context of Mikhail Gromov's programme on CAT(k) spaces under the name ''orbihedron''. Historically, orbifolds arose first as surfaces with singular points long before they were formally defined. One of the first classical examples arose in the theory of modular forms with the action of the modular group \mathrm(2,\Z) on the upper half-plane: a version of the Riemann–Roch theorem holds after the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Group
In mathematics, physics and chemistry, a space group is the symmetry group of an object in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of an object that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups. In crystallography, space groups are also called the crystallographic or Fedorov groups, and represent a description of the symmetry of the crystal. A definitive source regarding 3-dimensional space groups is the ''International Tables for Crystallography'' . History Space groups in 2 dimensions are the 17 wallpaper groups which have been known for several centuries, though the proof that the list was complete was only ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
35 Cubic Fibrifold Groups
{{Numberdis ...
35 or XXXV may refer to: * 35 (number), the natural number following 34 and preceding 36 * one of the years 35 BC, AD 35, 1935, 2035 * ''XXXV'' (album), a 2002 album by Fairport Convention * ''35xxxv'', a 2015 album by One Ok Rock * "35" (song), a 2021 song by New Zealand youth choir Ka Hao * "Thirty Five", a song by Karma to Burn from the album ''Almost Heathen'', 2001 * III-V, a type of semiconductor material A semiconductor is a material which has an electrical conductivity value falling between that of a conductor, such as copper, and an insulator, such as glass. Its resistivity falls as its temperature rises; metals behave in the opposite way. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Space Group
In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc, and alternatively called ''cubic close-packed'' or ccp) Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive unit cells often are not. Bravais lattices The three Bravais lattices in the cubic crystal system are: The primitive cubic lattice (cP) consists of one lattice point on each corner of the cube; this means each simple cubic unit cell has in total one lattice point. Each atom at a lattice point is then shared equally between eight adjacent cubes, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Space Group Lattices
Cubic may refer to: Science and mathematics * Cube (algebra), "cubic" measurement * Cube, a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex ** Cubic crystal system, a crystal system where the unit cell is in the shape of a cube * Cubic function, a polynomial function of degree three * Cubic equation, a polynomial equation (reducible to ''ax''3 + ''bx''2 + ''cx'' + ''d'' = 0) * Cubic form, a homogeneous polynomial of degree 3 * Cubic graph (mathematics - graph theory), a graph where all vertices have degree 3 * Cubic plane curve (mathematics), a plane algebraic curve ''C'' defined by a cubic equation * Cubic reciprocity (mathematics - number theory), a theorem analogous to quadratic reciprocity * Cubic surface, an algebraic surface in three-dimensional space * Cubic zirconia, in geology, a mineral that is widely synthesized for use as a diamond simulacra * CUBIC, a histology method Computing * Cubic IDE, a modular deve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetragonal Disphenoid Symmetry0
In crystallography, the tetragonal crystal system is one of the 7 crystal systems. Tetragonal crystal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the cube becomes a rectangular prism with a square base (''a'' by ''a'') and height (''c'', which is different from ''a''). Bravais lattices There are two tetragonal Bravais lattices: the primitive tetragonal and the body-centered tetragonal. The base-centered tetragonal lattice is equivalent to the primitive tetragonal lattice with a smaller unit cell, while the face-centered tetragonal lattice is equivalent to the body-centered tetragonal lattice with a smaller unit cell. Crystal classes The point groups that fall under this crystal system are listed below, followed by their representations in international notation, Schoenflies notation, orbifold notation, Coxeter notation and mineral examples.Hurlbut, Cornelius S.; Klein, Cornelis, 1985, ''Manual of Mineralogy'', 20th ed., pp. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrilateral Tree
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple (not self-intersecting), or complex (self-intersecting, or crossed). Simple quadrilaterals are either convex or concave. The interior angles of a simple (and planar) quadrilateral ''ABCD'' add up to 360 degrees of arc, that is :\angle A+\angle B+\angle C+\angle D=360^. This is a special case of the ''n''-gon interior angle sum formula: ''S'' = (''n'' − 2) × 180°. All non-self-crossing quadrilaterals tile the plane, b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
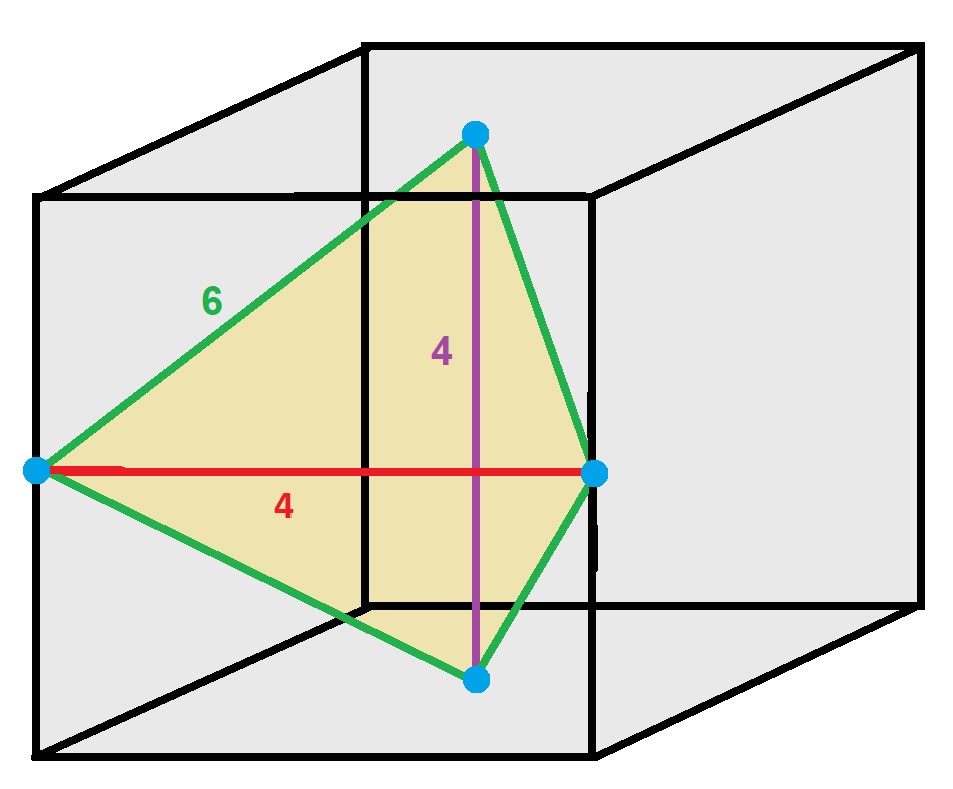
Tetragonal Disphenoid
In geometry, a disphenoid () is a tetrahedron whose four Face (geometry), faces are Congruence (geometry), congruent acute-angled triangles. It can also be described as a tetrahedron in which every two Edge (geometry), edges that are opposite each other have equal lengths. Other names for the same shape are isotetrahedron,. sphenoid,. bisphenoid, isosceles tetrahedron,. equifacial tetrahedron, almost regular tetrahedron, and tetramonohedron. All the solid angles and vertex figures of a disphenoid are the same, and the sum of the face angles at each vertex is equal to two right angles. However, a disphenoid is not a regular polyhedron, because, in general, its faces are not regular polygons, and its edges have three different lengths. Special cases and generalizations If the faces of a disphenoid are equilateral triangles, it is a regular tetrahedron with Td tetrahedral symmetry, although this is not normally called a disphenoid. When the faces of a disphenoid are isosceles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ''ABCD'' would be denoted . Characterizations A convex quadrilateral is a square if and only if it is any one of the following: * A rectangle with two adjacent equal sides * A rhombus with a right vertex angle * A rhombus with all angles equal * A parallelogram with one right vertex angle and two adjacent equal sides * A quadrilateral with four equal sides and four right angles * A quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other (i.e., a rhombus with equal diagonals) * A convex quadrilateral with successiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermann–Mauguin Notation
In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann (who introduced it in 1928) and the French mineralogist Charles-Victor Mauguin (who modified it in 1931). This notation is sometimes called international notation, because it was adopted as standard by the ''International Tables For Crystallography'' since their first edition in 1935. The Hermann–Mauguin notation, compared with the Schoenflies notation, is preferred in crystallography because it can easily be used to include translational symmetry elements, and it specifies the directions of the symmetry axes. Point groups Rotation axes are denoted by a number ''n'' — 1, 2, 3, 4, 5, 6, 7, 8 ... (angle of rotation ''φ'' = ). For improper rotations, Hermann–Mauguin symbols show rotoinversion axes, unlike Schoenflies and Shubnikov notations, that shows rotation-reflection axes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Notation
In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson. Reflectional groups For Coxeter groups, defined by pure reflections, there is a direct correspondence between the bracket notation and Coxeter-Dynkin diagram. The numbers in the bracket notation represent the mirror reflection orders in the branches of the Coxeter diagram. It uses the same simplification, suppressing 2s between orthogonal mirrors. The Coxeter notation is simplified with exponents to represent the number of branches in a row for linear diagram. So the ''A''''n'' group is represented by ''n''−1 to imply ''n'' nodes connected by ''n−1'' order-3 branches. Exampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
