|
Far-field Diffraction Pattern
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when plane waves are incident on a diffracting object, and the diffraction pattern is viewed at a sufficiently long distance (a distance satisfying Fraunhofer condition) from the object (in the far-field region), and also when it is viewed at the focal plane of an imaging lens. In contrast, the diffraction pattern created near the diffracting object (in the near field region) is given by the Fresnel diffraction equation. The equation was named in honor of Joseph von Fraunhofer although he was not actually involved in the development of the theory. This article explains where the Fraunhofer equation can be applied, and shows Fraunhofer diffraction patterns for various apertures. A detailed mathematical treatment of Fraunhofer diffraction is given in Fraunhofer diffraction equation. Equation When a beam of light is partly blocked by an obstacle, some of the light is scattered around the o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviolet, and infrared light. Because light is an electromagnetic wave, other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties. Most optical phenomena can be accounted for by using the classical electromagnetic description of light. Complete electromagnetic descriptions of light are, however, often difficult to apply in practice. Practical optics is usually done using simplified models. The most common of these, geometric optics, treats light as a collection of rays that travel in straight lines and bend when they pass through or reflect from surfaces. Physical optics is a more comprehensive model of light, which includes wave effects such as diffraction and interference that can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
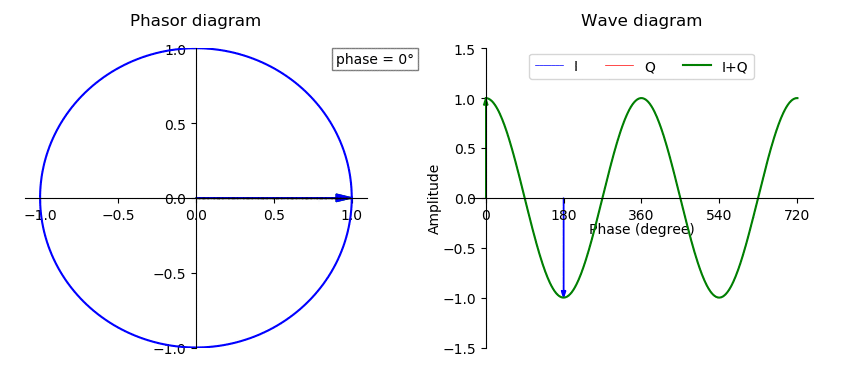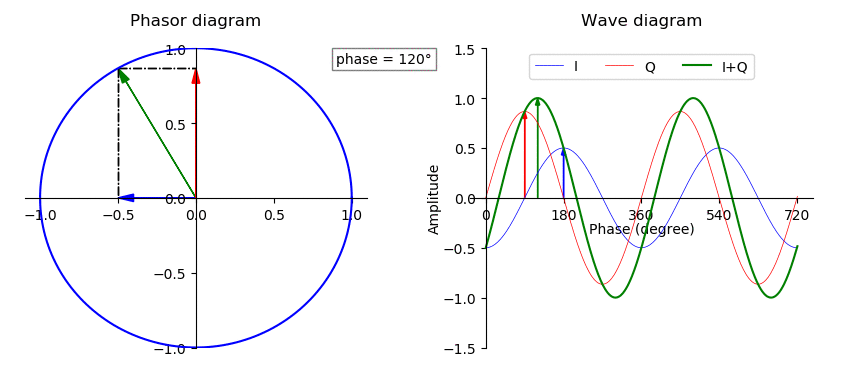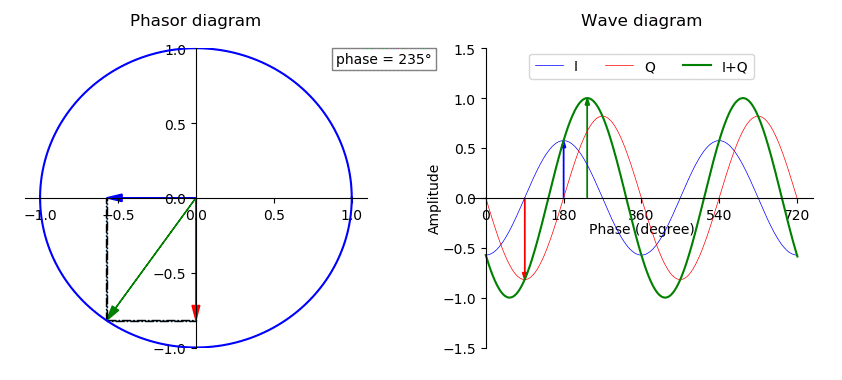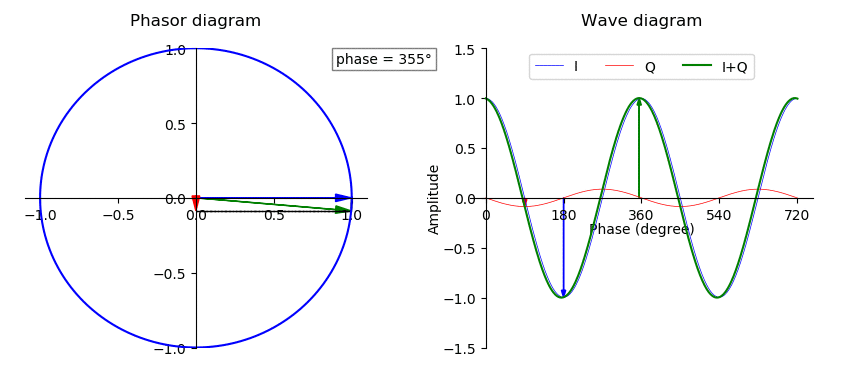
Vector Sum
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a ''directed line segment'', or graphically as an arrow connecting an ''initial point'' ''A'' with a ''terminal point'' ''B'', and denoted by \overrightarrow . A vector is what is needed to "carry" the point ''A'' to the point ''B''; the Latin word ''vector'' means "carrier". It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from ''A'' to ''B''. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors, operations w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectangular Diffraction
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containing a right angle. A rectangle with four sides of equal length is a ''square''. The term " oblong" is occasionally used to refer to a non-square rectangle. A rectangle with vertices ''ABCD'' would be denoted as . The word rectangle comes from the Latin ''rectangulus'', which is a combination of ''rectus'' (as an adjective, right, proper) and ''angulus'' (angle). A crossed rectangle is a crossed (self-intersecting) quadrilateral which consists of two opposite sides of a rectangle along with the two diagonals (therefore only two sides are parallel). It is a special case of an antiparallelogram, and its angles are not right angles and not all equal, though opposite angles are equal. Other geometries, such as spherical, elliptic, and hyperb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Field
An electric field (sometimes E-field) is the physical field that surrounds electrically charged particles and exerts force on all other charged particles in the field, either attracting or repelling them. It also refers to the physical field for a system of charged particles. Electric fields originate from electric charges and time-varying electric currents. Electric fields and magnetic fields are both manifestations of the electromagnetic field, one of the four fundamental interactions (also called forces) of nature. Electric fields are important in many areas of physics, and are exploited in electrical technology. In atomic physics and chemistry, for instance, the electric field is the attractive force holding the atomic nucleus and electrons together in atoms. It is also the force responsible for chemical bonding between atoms that result in molecules. The electric field is defined as a vector field that associates to each point in space the electrostatic (Coulomb) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase (waves)
In physics and mathematics, the phase of a periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is denoted \phi(t) and expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \phi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \phi(t) is also a periodic function, with the same period as F, that repeatedly scans the same range ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single Slit Diagram
Single may refer to: Arts, entertainment, and media * Single (music), a song release Songs * "Single" (Natasha Bedingfield song), 2004 * "Single" (New Kids on the Block and Ne-Yo song), 2008 * "Single" (William Wei song), 2016 * "Single", by Meghan Trainor from the album '' Only 17'' Sports * Single (baseball), the most common type of base hit * Single (cricket), point in cricket * Single (football), Canadian football point * Single-speed bicycle Transportation * Single-cylinder engine, an internal combustion engine design with one cylinder, or a motorcycle using such engine * Single (locomotive), a steam locomotive with a single pair of driving wheels * As a verb: to convert a double-track railway to a single-track railway Other uses * Single (mathematics) (1-tuple), a list or sequence with only one element * Single person, a person who is not in a committed relationship * Single precision, a computer numbering format that occupies one storage location in computer memory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Difraction Glass
Diffraction is defined as the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a secondary source of the propagating wave. Italian scientist Francesco Maria Grimaldi coined the word ''diffraction'' and was the first to record accurate observations of the phenomenon in 1660. In classical physics, the diffraction phenomenon is described by the Huygens–Fresnel principle that treats each point in a propagating wavefront as a collection of individual spherical wavelets. The characteristic bending pattern is most pronounced when a wave from a coherent source (such as a laser) encounters a slit/aperture that is comparable in size to its wavelength, as shown in the inserted image. This is due to the addition, or interference, of different points on the wavefront (or, equivalently, each wavelet) that travel by paths of di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single Slit Diffraction (english)
Single may refer to: Arts, entertainment, and media * Single (music), a song release Songs * "Single" (Natasha Bedingfield song), 2004 * "Single" (New Kids on the Block and Ne-Yo song), 2008 * "Single" (William Wei song), 2016 * "Single", by Meghan Trainor from the album '' Only 17'' Sports * Single (baseball), the most common type of base hit * Single (cricket), point in cricket * Single (football), Canadian football point * Single-speed bicycle Transportation * Single-cylinder engine, an internal combustion engine design with one cylinder, or a motorcycle using such engine * Single (locomotive), a steam locomotive with a single pair of driving wheels * As a verb: to convert a double-track railway to a single-track railway Other uses * Single (mathematics) (1-tuple), a list or sequence with only one element * Single person, a person who is not in a committed relationship * Single precision, a computer numbering format that occupies one storage location in computer memor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lens And Wavefronts Rotated
A lens is a transmissive optical device which focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (''elements''), usually arranged along a common axis. Lenses are made from materials such as glass or plastic, and are ground and polished or molded to a desired shape. A lens can focus light to form an image, unlike a prism, which refracts light without focusing. Devices that similarly focus or disperse waves and radiation other than visible light are also called lenses, such as microwave lenses, electron lenses, acoustic lenses, or explosive lenses. Lenses are used in various imaging devices like telescopes, binoculars and cameras. They are also used as visual aids in glasses to correct defects of vision such as myopia and hypermetropia. History The word ''lens'' comes from '' lēns'', the Latin name of the lentil (a seed of a lentil plant), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series, when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Cosines
In trigonometry, the law of cosines (also known as the cosine formula, cosine rule, or al-Kashi's theorem) relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states :c^2 = a^2 + b^2 - 2ab\cos\gamma, where denotes the angle contained between sides of lengths and and opposite the side of length . For the same figure, the other two relations are analogous: :a^2=b^2+c^2-2bc\cos\alpha, :b^2=a^2+c^2-2ac\cos\beta. The law of cosines generalizes the Pythagorean theorem, which holds only for right triangles: if the angle is a right angle (of measure 90 degrees, or radians), then , and thus the law of cosines reduces to the Pythagorean theorem: :c^2 = a^2 + b^2. The law of cosines is useful for computing the third side of a triangle when two sides and their enclosed angle are known. History Though the notion of the cosine was not yet developed in his time, Euclid's ''Elements'', dating back to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |