|
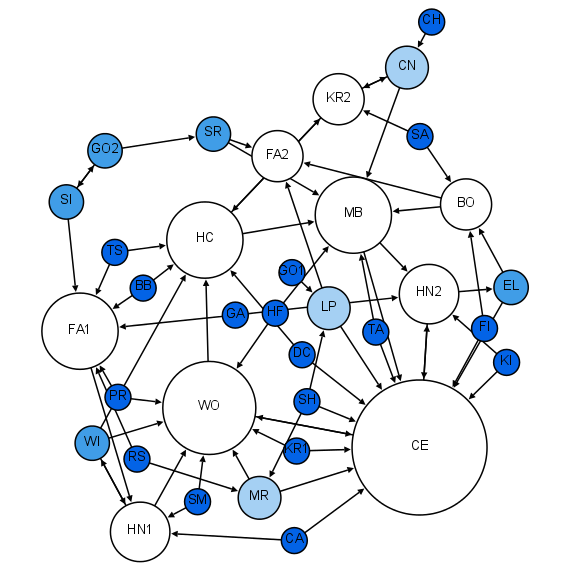
Exponential Random Graph Model
Exponential family random graph models (ERGMs) are a family of statistical models for analyzing data from social and other networks. Examples of networks examined using ERGM include knowledge networks, organizational networks, colleague networks, social media networks, networks of scientific development, and others. Background Many metrics exist to describe the structural features of an observed network such as the density, centrality, or assortativity. However, these metrics describe the observed network which is only one instance of a large number of possible alternative networks. This set of alternative networks may have similar or dissimilar structural features. To support statistical inference on the processes influencing the formation of network structure, a statistical model should consider the set of all possible alternative networks weighted on their similarity to an observed network. However because network data is inherently relational, it violates the assumptions of ind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Model
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of Sample (statistics), sample data (and similar data from a larger Statistical population, population). A statistical model represents, often in considerably idealized form, the data-generating process. A statistical model is usually specified as a mathematical relationship between one or more random variables and other non-random variables. As such, a statistical model is "a formal representation of a theory" (Herman J. Adèr, Herman Adèr quoting Kenneth A. Bollen, Kenneth Bollen). All Statistical hypothesis testing, statistical hypothesis tests and all Estimator, statistical estimators are derived via statistical models. More generally, statistical models are part of the foundation of statistical inference. Introduction Informally, a statistical model can be thought of as a statistical assumption (or set of statistical assumptions) with a certain property: that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Network
A social network is a social structure made up of a set of social actors (such as individuals or organizations), sets of dyadic ties, and other social interactions between actors. The social network perspective provides a set of methods for analyzing the structure of whole social entities as well as a variety of theories explaining the patterns observed in these structures. The study of these structures uses social network analysis to identify local and global patterns, locate influential entities, and examine network dynamics. Social networks and the analysis of them is an inherently interdisciplinary academic field which emerged from social psychology, sociology, statistics, and graph theory. Georg Simmel authored early structural theories in sociology emphasizing the dynamics of triads and "web of group affiliations". Jacob Moreno is credited with developing the first sociograms in the 1930s to study interpersonal relationships. These approaches were mathematically formalize ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Network Science
Network science is an academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks, considering distinct elements or actors represented by ''nodes'' (or ''vertices'') and the connections between the elements or actors as ''links'' (or ''edges''). The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena." Background and history The study of networks has emerged in diverse disciplines as a means of analyzing complex relational data. The earliest known paper in this f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Inference
Statistical inference is the process of using data analysis to infer properties of an underlying probability distribution, distribution of probability.Upton, G., Cook, I. (2008) ''Oxford Dictionary of Statistics'', OUP. . Inferential statistical analysis infers properties of a Statistical population, population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is Sampling (statistics), sampled from a larger population. Inferential statistics can be contrasted with descriptive statistics. Descriptive statistics is solely concerned with properties of the observed data, and it does not rest on the assumption that the data come from a larger population. In machine learning, the term ''inference'' is sometimes used instead to mean "make a prediction, by evaluating an already trained model"; in this context inferring properties of the model is referred to as ''training'' or ''learning'' (rather than ''inference''), and using a model for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Regression
In statistics, linear regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables). The case of one explanatory variable is called '' simple linear regression''; for more than one, the process is called multiple linear regression. This term is distinct from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable. In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimated from the data. Such models are called linear models. Most commonly, the conditional mean of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function of those values; less commonly, the conditional median or some other quantile is used. Like all forms of regression analysis, linear regression focuses on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree-preserving Randomization
Degree Preserving Randomization is a technique used in Network Science that aims to assess whether or not variations observed in a given graph could simply be an artifact of the graph's inherent structural properties rather than properties unique to the nodes, in an observed network. Background Cataloged as early as 1996, the simplest implementation of degree preserving randomization relies on a Monte Carlo algorithm that rearranges, or "rewires" the network at random such that, with a sufficient number of rewires, the network's degree distribution is identical to the initial degree distribution of the network, though the topological structure of the network has become completely distinct from the original network. Degree preserving randomization, while it has many different forms, typically takes on the form of a relatively simple approach: for any network consisting of N nodes with E edges, select two dyadically tied nodes. For each of these dyadic pairs, switch the edges su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Family
In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, including the enabling of the user to calculate expectations, covariances using differentiation based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman–Darmois family. The terms "distribution" and "family" are often used loosely: specifically, ''an'' exponential family is a ''set'' of distributions, where the specific distribution varies with the parameter; however, a parametric ''family'' of distributions is often referred to as "''a'' distribution" (like "the normal distribution", meaning "the family of normal distributions"), and the set of all exponential families is sometimes l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Graph
In mathematics, random graph is the general term to refer to probability distributions over graphs. Random graphs may be described simply by a probability distribution, or by a random process which generates them. The theory of random graphs lies at the intersection between graph theory and probability theory. From a mathematical perspective, random graphs are used to answer questions about the properties of ''typical'' graphs. Its practical applications are found in all areas in which complex networks need to be modeled – many random graph models are thus known, mirroring the diverse types of complex networks encountered in different areas. In a mathematical context, ''random graph'' refers almost exclusively to the Erdős–Rényi random graph model. In other contexts, any graph model may be referred to as a ''random graph''. Models A random graph is obtained by starting with a set of ''n'' isolated vertices and adding successive edges between them at random. The aim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sufficient Statistic
In statistics, a statistic is ''sufficient'' with respect to a statistical model and its associated unknown parameter if "no other statistic that can be calculated from the same sample provides any additional information as to the value of the parameter". In particular, a statistic is sufficient for a family of probability distributions if the sample from which it is calculated gives no additional information than the statistic, as to which of those probability distributions is the sampling distribution. A related concept is that of linear sufficiency, which is weaker than ''sufficiency'' but can be applied in some cases where there is no sufficient statistic, although it is restricted to linear estimators. The Kolmogorov structure function deals with individual finite data; the related notion there is the algorithmic sufficient statistic. The concept is due to Sir Ronald Fisher in 1920. Stephen Stigler noted in 1973 that the concept of sufficiency had fallen out of favor in des ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs Entropy
The concept entropy was first developed by German physicist Rudolf Clausius in the mid-nineteenth century as a thermodynamic property that predicts that certain spontaneous processes are irreversible or impossible. In statistical mechanics, entropy is formulated as a statistical property using probability theory. The statistical entropy perspective was introduced in 1870 by Austrian physicist Ludwig Boltzmann, who established a new field of physics that provided the descriptive linkage between the macroscopic observation of nature and the microscopic view based on the rigorous treatment of a large ensembles of microstates that constitute thermodynamic systems. Boltzmann's principle Ludwig Boltzmann defined entropy as a measure of the number of possible microscopic states (''microstates'') of a system in thermodynamic equilibrium, consistent with its macroscopic thermodynamic properties, which constitute the ''macrostate'' of the system. A useful illustration is the example of a sa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |