|
Elliptic Orbits
In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 (thus excluding the circular orbit). In a wider sense, it is a Kepler's orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1. In a gravitational two-body problem with negative energy, both bodies follow similar elliptic orbits with the same orbital period around their common barycenter. Also the relative position of one body with respect to the other follows an elliptic orbit. Examples of elliptic orbits include: Hohmann transfer orbit, Molniya orbit, and tundra orbit. Velocity Under standard assumptions, no other forces acting except two spherically symmetrical bodies m1 and m2, the orbital speed (v\,) of one body travel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
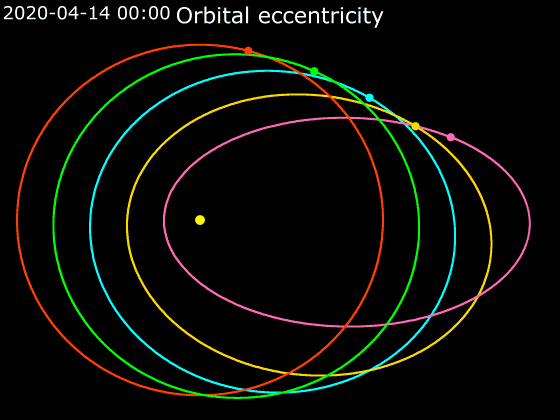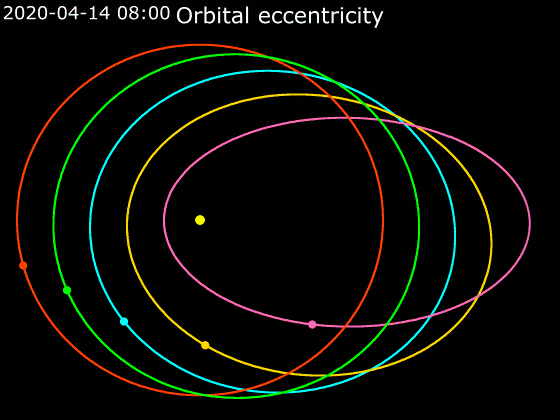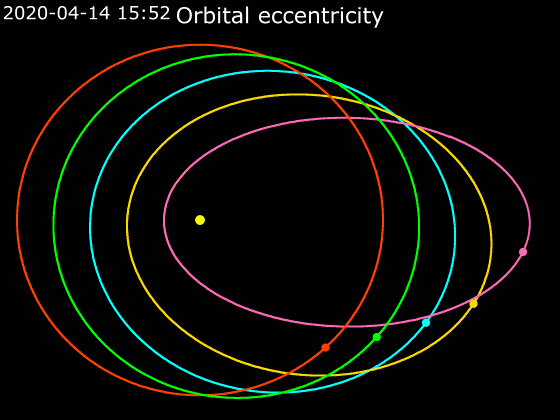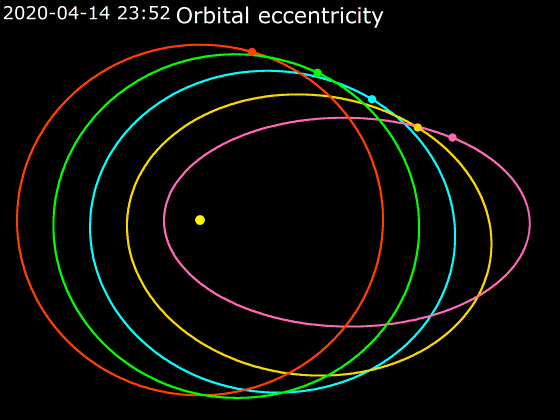
Animation Of Orbital Eccentricity
Animation is a method by which still figures are manipulated to appear as moving images. In traditional animation, images are drawn or painted by hand on transparent celluloid sheets to be photographed and exhibited on film. Today, most animations are made with computer-generated imagery (CGI). Computer animation can be very detailed 3D animation, while 2D computer animation (which may have the look of traditional animation) can be used for stylistic reasons, low bandwidth, or faster real-time renderings. Other common animation methods apply a stop motion technique to two- and three-dimensional objects like paper cutouts, puppets, or clay figures. A cartoon is an animated film, usually a short film, featuring an exaggerated visual style. The style takes inspiration from comic strips, often featuring anthropomorphic animals, superheroes, or the adventures of human protagonists. Especially with animals that form a natural predator/prey relationship (e.g. cats and mice, coyo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molniya Orbit
A Molniya orbit ( rus, Молния, p=ˈmolnʲɪjə, a=Ru-молния.ogg, "Lightning") is a type of satellite orbit designed to provide communications and remote sensing coverage over high latitudes. It is a highly elliptical orbit with an inclination of 63.4 degrees, an argument of perigee of 270 degrees, and an orbital period of approximately half a sidereal day. The name comes from the ''Molniya'' satellites, a series of Soviet/Russian civilian and military communications satellites which have used this type of orbit since the mid-1960s. The Molniya orbit has a long dwell time over the hemisphere of interest, while moving very quickly over the other. In practice, this places it over either Russia or Canada for the majority of its orbit, providing a high angle of view to communications and monitoring satellites covering these high-latitude areas. Geostationary orbits, which are necessarily inclined over the equator, can only view these regions from a low angle, hamperin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit Equation
In astrodynamics, an orbit equation defines the path of orbiting body m_2\,\! around central body m_1\,\! relative to m_1\,\!, without specifying position as a function of time. Under standard assumptions, a body moving under the influence of a force, directed to a central body, with a magnitude inversely proportional to the square of the distance (such as gravity), has an orbit that is a conic section (i.e. circular orbit, elliptic orbit, parabolic trajectory, hyperbolic trajectory, or radial trajectory) with the central body located at one of the two foci, or ''the'' focus ( Kepler's first law). If the conic section intersects the central body, then the actual trajectory can only be the part above the surface, but for that part the orbit equation and many related formulas still apply, as long as it is a freefall (situation of weightlessness). Central, inverse-square law force Consider a two-body system consisting of a central body of mass ''M'' and a much smaller, orbiting b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Relative Angular Momentum
In celestial mechanics, the specific relative angular momentum (often denoted \vec or \mathbf) of a body is the angular momentum of that body divided by its mass. In the case of two orbiting bodies it is the vector product of their relative position and relative linear momentum, divided by the mass of the body in question. Specific relative angular momentum plays a pivotal role in the analysis of the two-body problem, as it remains constant for a given orbit under ideal conditions. "Specific" in this context indicates angular momentum per unit mass. The SI unit for specific relative angular momentum is square meter per second. Definition The specific relative angular momentum is defined as the cross product of the relative position vector \mathbf and the relative velocity vector \mathbf . \mathbf = \mathbf\times \mathbf = \frac where \mathbf is the angular momentum vector, defined as \mathbf \times m \mathbf. The \mathbf vector is always perpendicular to the instantaneo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virial Theorem
In mechanics, the virial theorem provides a general equation that relates the average over time of the total kinetic energy of a stable system of discrete particles, bound by potential forces, with that of the total potential energy of the system. Mathematically, the theorem states \left\langle T \right\rangle = -\frac12\,\sum_^N \bigl\langle \mathbf_k \cdot \mathbf_k \bigr\rangle where is the total kinetic energy of the particles, represents the force on the th particle, which is located at position , and angle brackets represent the average over time of the enclosed quantity. The word virial for the right-hand side of the equation derives from ''vis'', the Latin word for "force" or "energy", and was given its technical definition by Rudolf Clausius in 1870. The significance of the virial theorem is that it allows the average total kinetic energy to be calculated even for very complicated systems that defy an exact solution, such as those considered in statistical mechanics; thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Central Body
A primary (also called a gravitational primary, primary body, or central body) is the main physical body of a gravitationally bound, multi-object system. This object constitutes most of that system's mass and will generally be located near the system's barycenter. In the Solar System, the Sun is the primary for all objects that orbit the star. In the same way, the primary of all satellites (be they natural satellites (moons) or artificial ones) is the planet they orbit. The term ''primary'' is often used to avoid specifying whether the object near the barycenter is a planet, a star, or any other astronomical object. In this sense, the word ''primary'' is always used as a noun. The center of mass is the average position of all the objects weighed by mass. The Sun is so massive that the Solar System's barycenter frequently lies very near the Sun's center but owing to the mass and distance of the gas giant planets, the Solar System's barycenter occasionally lies outside the Sun as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vis-viva Equation
In astrodynamics, the ''vis-viva'' equation, also referred to as orbital-energy-invariance law, is one of the equations that model the motion of orbiting bodies. It is the direct result of the principle of conservation of mechanical energy which applies when the only force acting on an object is its own weight. ''Vis viva'' (Latin for "living force") is a term from the history of mechanics, and it survives in this sole context. It represents the principle that the difference between the total work of the accelerating forces of a system and that of the retarding forces is equal to one half the ''vis viva'' accumulated or lost in the system while the work is being done. Equation For any Keplerian orbit (elliptic, parabolic, hyperbolic, or radial), the ''vis-viva'' equation is as follows: :v^2 = GM \left( - \right) where: * ''v'' is the relative speed of the two bodies * ''r'' is the distance between the two bodies centers of mass * ''a'' is the length of the semi-major axis ('' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Orbital Energy
In the gravitational two-body problem, the specific orbital energy \varepsilon (or vis-viva energy) of two orbiting bodies is the constant sum of their mutual potential energy (\varepsilon_p) and their total kinetic energy (\varepsilon_k), divided by the reduced mass. According to the orbital energy conservation equation (also referred to as vis-viva equation), it does not vary with time: \begin \varepsilon &= \varepsilon_k + \varepsilon_p \\ &= \frac - \frac = -\frac \frac \left(1 - e^2\right) = -\frac \end where *v is the relative orbital speed; *r is the orbital distance between the bodies; *\mu = (m_1 + m_2) is the sum of the standard gravitational parameters of the bodies; *h is the specific relative angular momentum in the sense of relative angular momentum divided by the reduced mass; *e is the orbital eccentricity; *a is the semi-major axis. It is expressed in MJ/kg or \frac. For an elliptic orbit the specific orbital energy is the neg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler's Laws Of Planetary Motion
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that: # The orbit of a planet is an ellipse with the Sun at one of the two foci. # A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. # The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law helps to establish that when a planet is closer to the Sun, it travels faster. The third law ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Trajectory
In astrodynamics or celestial mechanics, a hyperbolic trajectory or hyperbolic orbit is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one. Under simplistic assumptions a body traveling along this trajectory will coast towards infinity, settling to a final excess velocity relative to the central body. Similarly to parabolic trajectories, all hyperbolic trajectories are also escape trajectories. The specific energy of a hyperbolic trajectory orbit is positive. Planetary flybys, used for gravitational slingshots, can be described within the planet's sphere of influence using hyperbolic trajectories. Parameters describing a hyperbolic trajectory Like an elliptical orbit, a hyperbol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-major Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the center ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Gravitational Parameter
In celestial mechanics, the standard gravitational parameter ''μ'' of a celestial body is the product of the gravitational constant ''G'' and the mass ''M'' of the bodies. For two bodies the parameter may be expressed as G(m1+m2), or as GM when one body is much larger than the other. \mu=GM \ For several objects in the Solar System, the value of ''μ'' is known to greater accuracy than either ''G'' or ''M''. The SI units of the standard gravitational parameter are . However, units of are frequently used in the scientific literature and in spacecraft navigation. Definition Small body orbiting a central body The central body in an orbital system can be defined as the one whose mass (''M'') is much larger than the mass of the orbiting body (''m''), or . This approximation is standard for planets orbiting the Sun or most moons and greatly simplifies equations. Under Newton's law of universal gravitation, if the distance between the bodies is ''r'', the force exerted on the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |