elliptic orbits on:
[Wikipedia]
[Google]
[Amazon]
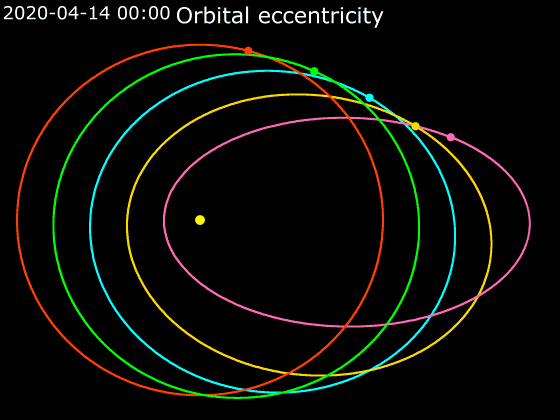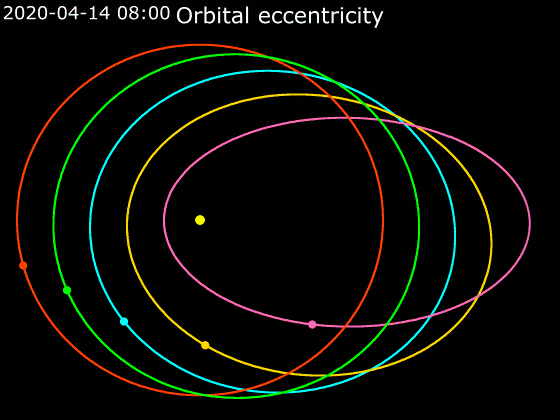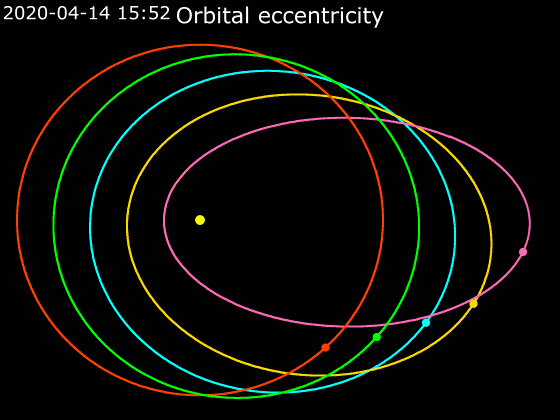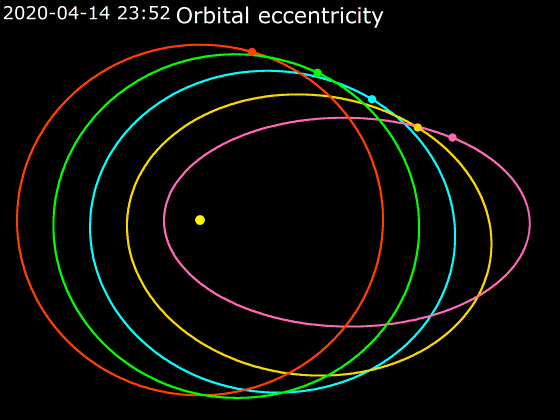 In astrodynamics or
In astrodynamics or
Java applet animating the orbit of a satellite
in an elliptic Kepler orbit around the Earth with any value for semi-major axis and eccentricity.
Lunar photographic comparison
Solar photographic comparison * http://www.castor2.ca {{Portal bar, Astronomy, Stars, Spaceflight, Outer space, Solar System Orbits
 In astrodynamics or
In astrodynamics or celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to ...
, an elliptical orbit or eccentric orbit is an orbit
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an ...
with an eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off-Centre (geometry), center, in geometry
* Eccentricity (g ...
of less than 1; this includes the special case of a circular orbit
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle.
In this case, not only the distance, but also the speed, angular speed, Potential energy, potential and kinetic energy are constant. T ...
, with eccentricity equal to 0. Some orbits have been referred to as "elongated orbits" if the eccentricity is "high" but that is not an explanatory term. For the simple two body problem, all orbits are ellipses.
In a gravitational two-body problem, both bodies follow similar elliptical orbits with the same orbital period around their common barycenter. The relative position of one body with respect to the other also follows an elliptic orbit.
Examples of elliptic orbits include Hohmann transfer orbits, Molniya orbits, and tundra orbits.
Velocity
Under standard assumptions, no other forces acting except two spherically symmetrical bodies and , theorbital speed
In gravitationally bound systems, the orbital speed of an astronomical body or object (e.g. planet, moon, artificial satellite, spacecraft, or star) is the speed at which it orbits around either the barycenter (the combined center of mass) or ...
() of one body traveling along an elliptical orbit can be computed from the vis-viva equation as:
:
where:
* is the standard gravitational parameter
The standard gravitational parameter ''μ'' of a celestial body is the product of the gravitational constant ''G'' and the mass ''M'' of that body. For two bodies, the parameter may be expressed as , or as when one body is much larger than the ...
, , often expressed as when one body is much larger than the other.
* is the distance between the orbiting body and center of mass.
* is the length of the semi-major axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longe ...
.
The velocity equation for a hyperbolic trajectory
In astrodynamics or celestial mechanics, a hyperbolic trajectory or hyperbolic orbit is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the ...
has either , or it is the same with the convention that in that case is negative.
Orbital period
Under standard assumptions the orbital period () of a body travelling along an elliptic orbit can be computed as: : where: * is thestandard gravitational parameter
The standard gravitational parameter ''μ'' of a celestial body is the product of the gravitational constant ''G'' and the mass ''M'' of that body. For two bodies, the parameter may be expressed as , or as when one body is much larger than the ...
.
* is the length of the semi-major axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longe ...
.
Conclusions:
*The orbital period is equal to that for a circular orbit
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle.
In this case, not only the distance, but also the speed, angular speed, Potential energy, potential and kinetic energy are constant. T ...
with the orbital radius equal to the semi-major axis (),
*For a given semi-major axis the orbital period does not depend on the eccentricity (See also: Kepler's third law).
Energy
Under standard assumptions, thespecific orbital energy
In the gravitational two-body problem, the specific orbital energy \varepsilon (or specific ''vis-viva'' energy) of two orbiting bodies is the constant quotient of their mechanical energy (the sum of their mutual potential energy, \varepsilon ...
() of an elliptic orbit is negative and the orbital energy conservation equation (the Vis-viva equation) for this orbit can take the form:
:
where:
* is the orbital speed
In gravitationally bound systems, the orbital speed of an astronomical body or object (e.g. planet, moon, artificial satellite, spacecraft, or star) is the speed at which it orbits around either the barycenter (the combined center of mass) or ...
of the orbiting body,
* is the distance of the orbiting body from the central body,
* is the length of the semi-major axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longe ...
,
* is the standard gravitational parameter
The standard gravitational parameter ''μ'' of a celestial body is the product of the gravitational constant ''G'' and the mass ''M'' of that body. For two bodies, the parameter may be expressed as , or as when one body is much larger than the ...
.
Conclusions:
*For a given semi-major axis the specific orbital energy is independent of the eccentricity.
Using the virial theorem to find:
*the time-average of the specific potential energy is equal to −2ε
**the time-average of ''r''−1 is ''a''−1
*the time-average of the specific kinetic energy is equal to ε
Energy in terms of semi major axis
It can be helpful to know the energy in terms of the semi major axis (and the involved masses). The total energy of the orbit is given by :, where a is the semi major axis.Derivation
Since gravity is a central force, the angular momentum is constant: : At the closest and furthest approaches, the angular momentum is perpendicular to the distance from the mass orbited, therefore: :. The total energy of the orbit is given by :. Substituting for v, the equation becomes :. This is true for r being the closest / furthest distance so two simultaneous equations are made, which when solved for E: : Since and , where epsilon is the eccentricity of the orbit, the stated result is reached.Flight path angle
The flight path angle is the angle between the orbiting body's velocity vector (equal to the vector tangent to the instantaneous orbit) and the local horizontal. Under standard assumptions of the conservation of angular momentum the flight path angle satisfies the equation: : where: * is the specific relative angular momentum of the orbit, * is theorbital speed
In gravitationally bound systems, the orbital speed of an astronomical body or object (e.g. planet, moon, artificial satellite, spacecraft, or star) is the speed at which it orbits around either the barycenter (the combined center of mass) or ...
of the orbiting body,
* is the radial distance of the orbiting body from the central body,
* is the flight path angle
is the angle between the orbital velocity vector and the semi-major axis. is the local true anomaly. , therefore,
:
:
where is the eccentricity.
The angular momentum is related to the vector cross product of position and velocity, which is proportional to the sine of the angle between these two vectors. Here is defined as the angle which differs by 90 degrees from this, so the cosine appears in place of the sine.
Equation of motion
From initial position and velocity
An orbit equation defines the path of an orbiting body around central body relative to , without specifying position as a function of time. If the eccentricity is less than 1 then the equation of motion describes an elliptical orbit. BecauseKepler's equation
In orbital mechanics, Kepler's equation relates various geometric properties of the orbit of a body subject to a central force.
It was derived by Johannes Kepler in 1609 in Chapter 60 of his ''Astronomia nova'', and in book V of his ''Epitome of ...
has no general closed-form solution for the Eccentric anomaly (E) in terms of the Mean anomaly (M), equations of motion as a function of time also have no closed-form solution (although numerical solutions exist for both).
However, closed-form time-independent path equations of an elliptic orbit with respect to a central body can be determined from just an initial position () and velocity ().
For this case it is convenient to use the following assumptions which differ somewhat from the standard assumptions above:
:# The central body's position is at the origin and is the primary focus () of the ellipse (alternatively, the center of mass may be used instead if the orbiting body has a significant mass)
:# The central body's mass (m1) is known
:# The orbiting body's initial position() and velocity() are known
:# The ellipse lies within the XY-plane
The fourth assumption can be made without loss of generality because any three points (or vectors) must lie within a common plane. Under these assumptions the second focus (sometimes called the "empty" focus) must also lie within the XY-plane: .
Using vectors
The general equation of an ellipse under these assumptions using vectors is: : where: * is the length of thesemi-major axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longe ...
.
* is the second ("empty") focus.
* is any (x,y) value satisfying the equation.
The semi-major axis length (a) can be calculated as:
:
where is the standard gravitational parameter
The standard gravitational parameter ''μ'' of a celestial body is the product of the gravitational constant ''G'' and the mass ''M'' of that body. For two bodies, the parameter may be expressed as , or as when one body is much larger than the ...
.
The empty focus () can be found by first determining the Eccentricity vector:
:
Where is the specific angular momentum of the orbiting body:
:
Then
:
Using XY Coordinates
This can be done in cartesian coordinates using the following procedure: The general equation of an ellipse under the assumptions above is: : Given: : the initial position coordinates : the initial velocity coordinates and : the gravitational parameter Then: : specific angular momentum : initial distance from F1 (at the origin) : the semi-major axis length : the Eccentricity vector coordinates : Finally, the empty focus coordinates : : Now the result values ''fx, fy'' and ''a'' can be applied to the general ellipse equation above.Orbital parameters
The state of an orbiting body at any given time is defined by the orbiting body's position and velocity with respect to the central body, which can be represented by the three-dimensionalCartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
(position of the orbiting body represented by x, y, and z) and the similar Cartesian components of the orbiting body's velocity. This set of six variables, together with time, are called the orbital state vectors
In astrodynamics and celestial dynamics, the orbital state vectors (sometimes state vectors) of an orbit are
cartesian coordinate system, Cartesian vectors of position (vector), position (\mathbf) and velocity (\mathbf) that together with their t ...
. Given the masses of the two bodies they determine the full orbit. The two most general cases with these 6 degrees of freedom are the elliptic and the hyperbolic orbit. Special cases with fewer degrees of freedom are the circular and parabolic orbit.
Because at least six variables are absolutely required to completely represent an elliptic orbit with this set of parameters, then six variables are required to represent an orbit with any set of parameters. Another set of six parameters that are commonly used are the orbital elements
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same o ...
.
Solar System
In theSolar System
The Solar SystemCapitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Sola ...
, planet
A planet is a large, Hydrostatic equilibrium, rounded Astronomical object, astronomical body that is generally required to be in orbit around a star, stellar remnant, or brown dwarf, and is not one itself. The Solar System has eight planets b ...
s, asteroid
An asteroid is a minor planet—an object larger than a meteoroid that is neither a planet nor an identified comet—that orbits within the Solar System#Inner Solar System, inner Solar System or is co-orbital with Jupiter (Trojan asteroids). As ...
s, most comet
A comet is an icy, small Solar System body that warms and begins to release gases when passing close to the Sun, a process called outgassing. This produces an extended, gravitationally unbound atmosphere or Coma (cometary), coma surrounding ...
s, and some pieces of space debris
Space debris (also known as space junk, space pollution, space waste, space trash, space garbage, or cosmic debris) are defunct human-made objects in spaceprincipally in Earth orbitwhich no longer serve a useful function. These include dere ...
have approximately elliptical orbits around the Sun. Strictly speaking, both bodies revolve around the same focus of the ellipse, the one closer to the more massive body, but when one body is significantly more massive, such as the sun in relation to the earth, the focus may be contained within the larger massing body, and thus the smaller is said to revolve around it. The following chart of the perihelion and aphelion of the planet
A planet is a large, Hydrostatic equilibrium, rounded Astronomical object, astronomical body that is generally required to be in orbit around a star, stellar remnant, or brown dwarf, and is not one itself. The Solar System has eight planets b ...
s, dwarf planet
A dwarf planet is a small planetary-mass object that is in direct orbit around the Sun, massive enough to be hydrostatic equilibrium, gravitationally rounded, but insufficient to achieve clearing the neighbourhood, orbital dominance like the ...
s, and Halley's Comet
Halley's Comet is the only known List of periodic comets, short-period comet that is consistently visible to the naked eye from Earth, appearing every 72–80 years, though with the majority of recorded apparitions (25 of 30) occurring after ...
demonstrates the variation of the eccentricity of their elliptical orbits. For similar distances from the sun, wider bars denote greater eccentricity. Note the almost-zero eccentricity of Earth and Venus compared to the enormous eccentricity of Halley's Comet and Eris.
Radial elliptic trajectory
A radial trajectory can be a double line segment, which is a degenerate ellipse with semi-minor axis = 0 and eccentricity = 1. Although the eccentricity is 1, this is not a parabolic orbit. Most properties and formulas of elliptic orbits apply. However, the orbit cannot be closed. It is an open orbit corresponding to the part of the degenerate ellipse from the moment the bodies touch each other and move away from each other until they touch each other again. In the case of point masses one full orbit is possible, starting and ending with a singularity. The velocities at the start and end are infinite in opposite directions and the potential energy is equal to minus infinity. The radial elliptic trajectory is the solution of a two-body problem with at some instant zero speed, as in the case of dropping an object (neglecting air resistance).History
The Babylonians were the first to realize that the Sun's motion along theecliptic
The ecliptic or ecliptic plane is the orbital plane of Earth's orbit, Earth around the Sun. It was a central concept in a number of ancient sciences, providing the framework for key measurements in astronomy, astrology and calendar-making.
Fr ...
was not uniform, though they were unaware of why this was; it is today known that this is due to the Earth moving in an elliptic orbit around the Sun, with the Earth moving faster when it is nearer to the Sun at perihelion and moving slower when it is farther away at aphelion.
In the 17th century, Johannes Kepler
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best know ...
discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun at one focus, and described this in his first law of planetary motion. Later, Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
explained this as a corollary of his law of universal gravitation.
See also
* Apsis * Characteristic energy *Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
* List of orbits
* Orbital eccentricity
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values be ...
* Orbit equation
* Parabolic trajectory
In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the Orbital eccentricity, eccentricity equal to 1 and is an unbound orbit that is exactly on the border between elliptical and hyperbolic. When moving away f ...
References
Sources
* * *External links
Java applet animating the orbit of a satellite
in an elliptic Kepler orbit around the Earth with any value for semi-major axis and eccentricity.
Lunar photographic comparison
Solar photographic comparison * http://www.castor2.ca {{Portal bar, Astronomy, Stars, Spaceflight, Outer space, Solar System Orbits