|
Exchange Operator
In quantum mechanics, the exchange operator \hat, also known as permutation operator, is a quantum mechanical operator that acts on states in Fock space. The exchange operator acts by switching the labels on any two identical particles described by the joint position quantum state \left, x_1, x_2\right\rangle. Since the particles are identical, the notion of exchange symmetry requires that the exchange operator be unitary. Construction In three or higher dimensions, the exchange operator can represent a literal exchange of the positions of the pair of particles by motion of the particles in an adiabatic process, with all other particles held fixed. Such motion is often not carried out in practice. Rather, the operation is treated as a "what if" similar to a parity inversion or time reversal operation. Consider two repeated operations of such a particle exchange: :\hat^2\left, x_1, x_2\right\rangle = \hat\left, x_2, x_1\right\rangle = \left, x_1, x_2\right\rangle There ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin–statistics Theorem
In quantum mechanics, the spin–statistics theorem relates the intrinsic spin of a particle (angular momentum not due to the orbital motion) to the particle statistics it obeys. In units of the reduced Planck constant ''ħ'', all particles that move in 3 dimensions have either integer spin or half-integer spin. Background Quantum states and indistinguishable particles In a quantum system, a physical state is described by a state vector. A pair of distinct state vectors are physically equivalent if they differ only by an overall phase factor, ignoring other interactions. A pair of indistinguishable particles such as this have only one state. This means that if the positions of the particles are exchanged (i.e., they undergo a permutation), this does not identify a new physical state, but rather one matching the original physical state. In fact, one cannot tell which particle is in which position. While the physical state does not change under the exchange of the particles' po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exchange Interaction
In chemistry and physics, the exchange interaction (with an exchange energy and exchange term) is a quantum mechanical effect that only occurs between identical particles. Despite sometimes being called an exchange force in an analogy to classical force, it is not a true force as it lacks a force carrier. The effect is due to the wave function of indistinguishable particles being subject to exchange symmetry, that is, either remaining unchanged (symmetric) or changing sign (antisymmetric) when two particles are exchanged. Both bosons and fermions can experience the exchange interaction. For fermions, this interaction is sometimes called Pauli repulsion and is related to the Pauli exclusion principle. For bosons, the exchange interaction takes the form of an effective attraction that causes identical particles to be found closer together, as in Bose–Einstein condensation. The exchange interaction alters the expectation value of the distance when the wave functions of two or more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavefunction
A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements made on the system can be derived from it. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi, respectively). The wave function is a function of the degrees of freedom corresponding to some maximal set of commuting observables. Once such a representation is chosen, the wave function can be derived from the quantum state. For a given system, the choice of which commuting degrees of freedom to use is not unique, and correspondingly the domain of the wave function is also not unique. For instance, it may be taken to be a function of all the position coordinates of the particles over position space, or the momenta of all the particles over momentum space; the two are related by a Fourier trans ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exchange Interaction
In chemistry and physics, the exchange interaction (with an exchange energy and exchange term) is a quantum mechanical effect that only occurs between identical particles. Despite sometimes being called an exchange force in an analogy to classical force, it is not a true force as it lacks a force carrier. The effect is due to the wave function of indistinguishable particles being subject to exchange symmetry, that is, either remaining unchanged (symmetric) or changing sign (antisymmetric) when two particles are exchanged. Both bosons and fermions can experience the exchange interaction. For fermions, this interaction is sometimes called Pauli repulsion and is related to the Pauli exclusion principle. For bosons, the exchange interaction takes the form of an effective attraction that causes identical particles to be found closer together, as in Bose–Einstein condensation. The exchange interaction alters the expectation value of the distance when the wave functions of two or more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of Molecule, molecules, Material, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed Wave function, wave functions as well as to observable properties such as structures, spectra, and thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics. Chemists rely heavily on spectroscopy through which information regarding the Quantization (physics), quantization of energy on a molecular scale can be obtained. Common metho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
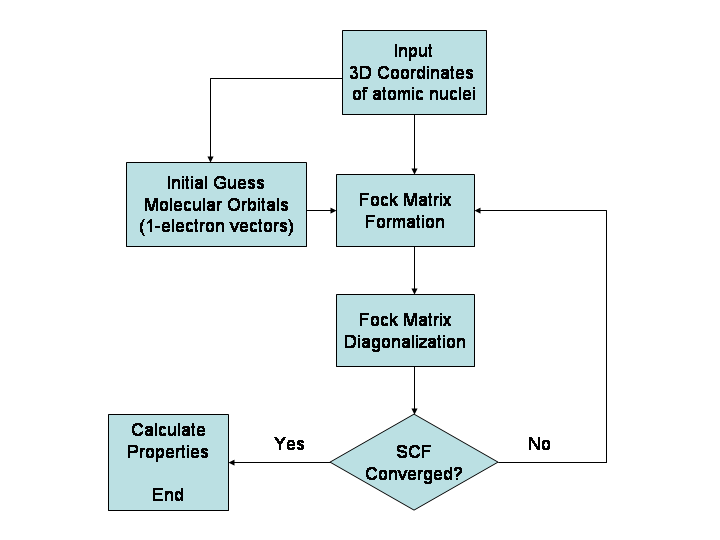
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distribution to be "s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anyon
In physics, an anyon is a type of quasiparticle that occurs only in two-dimensional systems, with properties much less restricted than the two kinds of standard elementary particles, fermions and bosons. In general, the operation of exchanging two identical particles, although it may cause a global phase shift, cannot affect observables. Anyons are generally classified as ''abelian'' or ''non-abelian''. Abelian anyons (detected by two experiments in 2020) play a major role in the fractional quantum Hall effect. Non-abelian anyons have not been definitively detected, although this is an active area of research. Introduction The statistical mechanics of large many-body systems obeys laws described by Maxwell–Boltzmann statistics. Quantum statistics is more complicated because of the different behaviors of two different kinds of particles called fermions and bosons. Quoting a recent, simple description:In the three-dimensional world we live in, there are only two types of p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antisymmetrizer
In quantum mechanics, an antisymmetrizer \mathcal (also known as antisymmetrizing operatorP.A.M. Dirac, ''The Principles of Quantum Mechanics'', 4th edition, Clarendon, Oxford UK, (1958) p. 248) is a linear operator that makes a wave function of ''N'' identical fermions antisymmetric under the exchange of the coordinates of any pair of fermions. After application of \mathcal the wave function satisfies the Pauli exclusion principle. Since \mathcal is a projection operator, application of the antisymmetrizer to a wave function that is already totally antisymmetric has no effect, acting as the identity operator. Mathematical definition Consider a wave function depending on the space and spin coordinates of ''N'' fermions: : \Psi(1,2, \ldots, N)\quad\text \quad i \leftrightarrow (\mathbf_i, \sigma_i), where the position vector r''i'' of particle ''i'' is a vector in \mathbb^3 and σi takes on 2''s''+1 values, where ''s'' is the half-integral intrinsic spin of the fermion. For ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conserved Quantity
In mathematics, a conserved quantity of a dynamical system is a function of the dependent variables, the value of which remains constant along each trajectory of the system. Not all systems have conserved quantities, and conserved quantities are not unique, since one can always produce another such quantity by applying a suitable function, such as adding a constant, to a conserved quantity. Since many laws of physics express some kind of conservation, conserved quantities commonly exist in mathematical models of physical systems. For example, any classical mechanics model will have mechanical energy as a conserved quantity as long as the forces involved are conservative. Differential equations For a first order system of differential equations :\frac = \mathbf f(\mathbf r, t) where bold indicates vector quantities, a scalar-valued function ''H''(r) is a conserved quantity of the system if, for all time and initial conditions in some specific domain, :\frac = 0 Note that by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system ** Dyall Hamiltonian, a modified Hamiltonian with two-electron nature ** Molecular Hamiltonian, the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule * Hamiltonian (control theory), a function used to solve a problem of optimal control for a dynamical system * Hamiltonian path, a path in a graph that visits each vertex exactly once * Hamiltonian group, a non-abelian group the subgroups of which are all normal * Hamiltonian economic program, the economic policies advocated by Alexander Hamilton, the first United States Secretary of the Treasury See also * Alexander Hamilton (1755 or 1757–1804), American statesman and one of the Founding Fathers of the US * Hamilton (other) Hamilton may refer to: People * Hamilton (name), a common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin (physics)
Spin is a conserved quantity carried by elementary particles, and thus by composite particles (hadrons) and atomic nucleus, atomic nuclei. Spin is one of two types of angular momentum in quantum mechanics, the other being ''orbital angular momentum''. The orbital angular momentum operator is the quantum-mechanical counterpart to the classical angular momentum of orbital revolution and appears when there is periodic structure to its wavefunction as the angle varies. For photons, spin is the quantum-mechanical counterpart of the Polarization (waves), polarization of light; for electrons, the spin has no classical counterpart. The existence of electron spin angular momentum is inferred from experiments, such as the Stern–Gerlach experiment, in which silver atoms were observed to possess two possible discrete angular momenta despite having no orbital angular momentum. The existence of the electron spin can also be inferred theoretically from the spin–statistics theorem and from th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |