|
Errors-in-variables
In statistics, an errors-in-variables model or a measurement error model is a regression model that accounts for measurement errors in the independent variables. In contrast, standard regression models assume that those regressors have been measured exactly, or observed without error; as such, those models account only for errors in the dependent variables, or responses. In the case when some regressors have been measured with errors, estimation based on the standard assumption leads to inconsistent estimates, meaning that the parameter estimates do not tend to the true values even in very large samples. For simple linear regression the effect is an underestimate of the coefficient, known as the '' attenuation bias''. In non-linear models the direction of the bias is likely to be more complicated. Motivating example Consider a simple linear regression model of the form : y_ = \alpha + \beta x_^ + \varepsilon_t\,, \quad t=1,\ldots,T, where x_^ denotes the ''true'' bu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regression Dilution
Regression dilution, also known as regression attenuation, is the biasing of the linear regression slope towards zero (the underestimation of its absolute value), caused by errors in the independent variable. Consider fitting a straight line for the relationship of an outcome variable ''y'' to a predictor variable ''x'', and estimating the slope of the line. Statistical variability, measurement error or random noise in the ''y'' variable causes uncertainty in the estimated slope, but not bias: on average, the procedure calculates the right slope. However, variability, measurement error or random noise in the ''x'' variable causes bias in the estimated slope (as well as imprecision). The greater the variance in the ''x'' measurement, the closer the estimated slope must approach zero instead of the true value. It may seem counter-intuitive that noise in the predictor variable ''x'' induces a bias, but noise in the outcome variable ''y'' does not. Recall that linear regressi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Attenuation Bias
Regression dilution, also known as regression attenuation, is the biasing of the linear regression slope towards zero (the underestimation of its absolute value), caused by errors in the independent variable. Consider fitting a straight line for the relationship of an outcome variable ''y'' to a predictor variable ''x'', and estimating the slope of the line. Statistical variability, measurement error or random noise in the ''y'' variable causes uncertainty in the estimated slope, but not bias: on average, the procedure calculates the right slope. However, variability, measurement error or random noise in the ''x'' variable causes bias in the estimated slope (as well as imprecision). The greater the variance in the ''x'' measurement, the closer the estimated slope must approach zero instead of the true value. It may seem counter-intuitive that noise in the predictor variable ''x'' induces a bias, but noise in the outcome variable ''y'' does not. Recall that linear regression is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Visualization Of Errors-in-variables Linear Regression
Visualization or visualisation may refer to: *Visualization (graphics), the physical or imagining creation of images, diagrams, or animations to communicate a message * Data and information visualization, the practice of creating visual representations of complex data and information * Music visualization, animated imagery based on a piece of music *Mental image, the experience of images without the relevant external stimuli * "Visualization", a song by Blank Banshee on the 2012 album ''Blank Banshee 0'' See also * Creative visualization (other) * Visualizer (other) * * * * Graphics * List of graphical methods, various forms of visualization * Guided imagery, a mind-body intervention by a trained practitioner * Illustration, a decoration, interpretation or visual explanation of a text, concept or process * Image, an artifact that depicts visual perception, such as a photograph or other picture * Infographics {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latent Variable Model
A latent variable model is a statistical model that relates a set of observable variables (also called ''manifest variables'' or ''indicators'') to a set of latent variables. Latent variable models are applied across a wide range of fields such as biology, computer science, and social science. Common use cases for latent variable models include applications in psychometrics (e.g., summarizing responses to a set of survey questions with a factor analysis model positing a smaller number of psychological attributes, such as the trait extraversion, that are presumed to cause the survey question responses), and natural language processing (e.g., a topic model summarizing a corpus of texts with a number of "topics"). It is assumed that the responses on the indicators or manifest variables are the result of an individual's position on the latent variable(s), and that the manifest variables have nothing in common after controlling for the latent variable ( local independence). Different ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dummy Variable (statistics)
In regression analysis, a dummy variable (also known as indicator variable or just dummy) is one that takes a binary value (0 or 1) to indicate the absence or presence of some categorical effect that may be expected to shift the outcome. For example, if we were studying the relationship between biological sex and income, we could use a dummy variable to represent the sex of each individual in the study. The variable could take on a value of 1 for males and 0 for females (or vice versa). In machine learning this is known as one-hot encoding. Dummy variables are commonly used in regression analysis to represent categorical variables that have more than two levels, such as education level or occupation. In this case, multiple dummy variables would be created to represent each level of the variable, and only one dummy variable would take on a value of 1 for each observation. Dummy variables are useful because they allow us to include categorical variables in our analysis, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
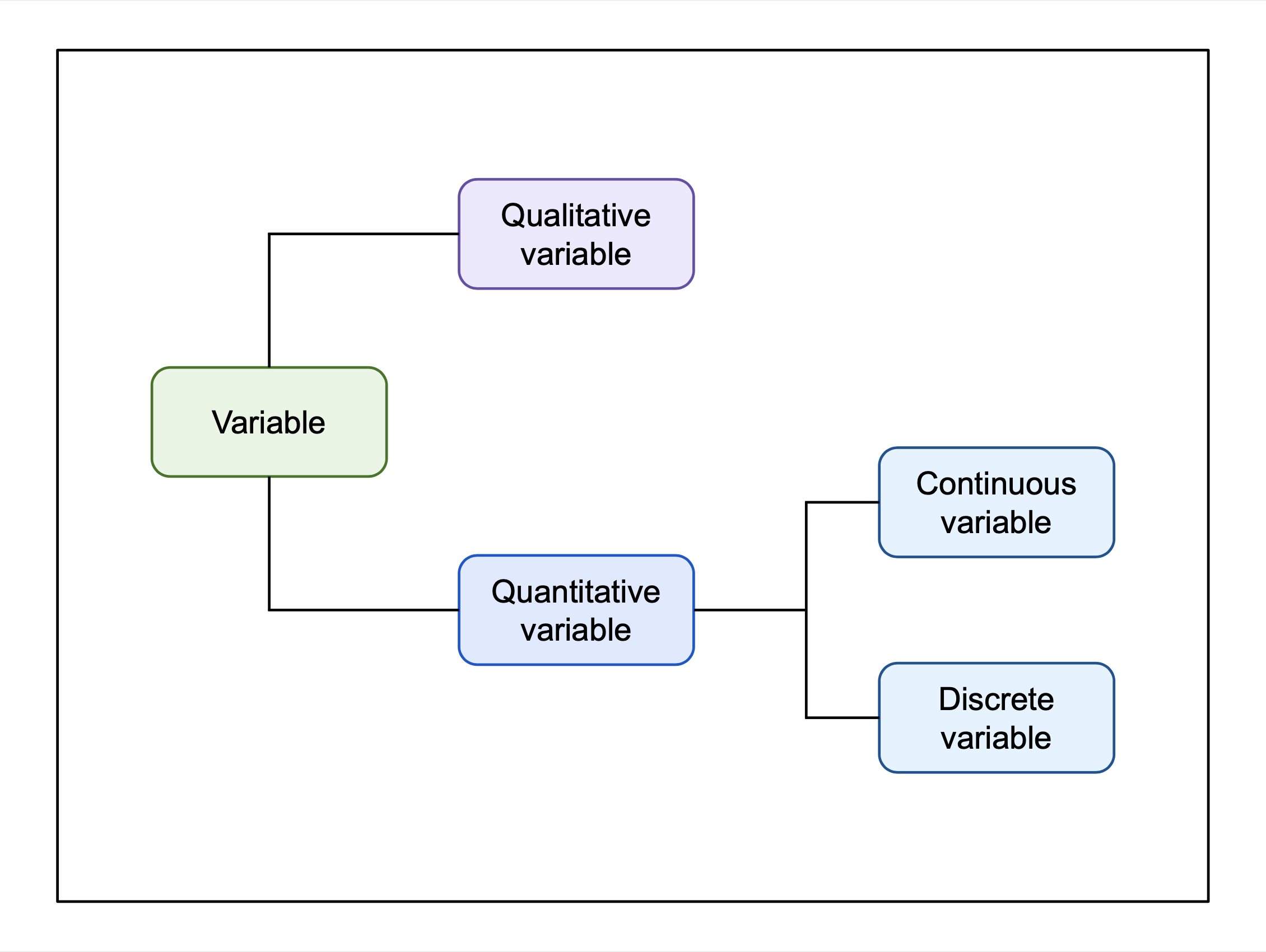
Continuous And Discrete Variables
In mathematics and statistics, a quantitative variable may be continuous or discrete. If it can take on two real values and all the values between them, the variable is continuous in that interval. If it can take on a value such that there is a non-infinitesimal gap on each side of it containing no values that the variable can take on, then it is discrete around that value. In some contexts, a variable can be discrete in some ranges of the number line and continuous in others. In statistics, continuous and discrete variables are distinct statistical data types which are described with different probability distributions. Continuous variable A continuous variable is a variable such that there are possible values between any two values. For example, a variable over a non-empty range of the real numbers is continuous if it can take on any value in that range. Methods of calculus are often used in problems in which the variables are continuous, for example in continuous optimi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Berkson Error Model
The Berkson error model is a description of random error (or misclassification) in measurement. Unlike classical error, Berkson error causes little or no bias in the measurement. It was proposed by Joseph Berkson in an article entitled “Are there two regressions?,” published in 1950. An example of Berkson error arises in exposure assessment in epidemiological studies. Berkson error may predominate over classical error in cases where exposure data are highly aggregated. While this kind of error reduces the power of a study, risk estimates themselves are not themselves attenuated (as would be the case where random error Observational error (or measurement error) is the difference between a measured value of a quantity and its unknown true value.Dodge, Y. (2003) ''The Oxford Dictionary of Statistical Terms'', OUP. Such errors are inherent in the measurement ... predominates). References Further reading * * Accuracy and precision Statistical deviation and dispe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
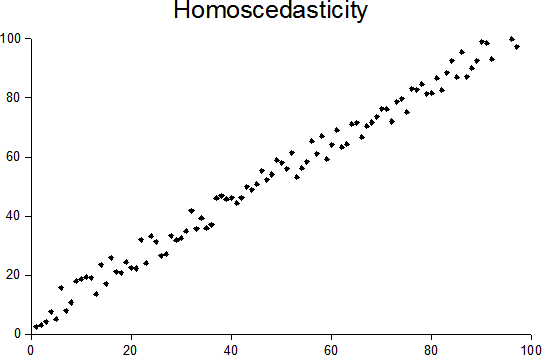
Heteroscedasticity
In statistics, a sequence of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as heterogeneity of variance. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. “Skedasticity” comes from the Ancient Greek word “skedánnymi”, meaning “to scatter”. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independence (probability Theory)
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two event (probability theory), events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of one does not affect the probability of occurrence of the other or, equivalently, does not affect the odds. Similarly, two random variables are independent if the realization of one does not affect the probability distribution of the other. When dealing with collections of more than two events, two notions of independence need to be distinguished. The events are called Pairwise independence, pairwise independent if any two events in the collection are independent of each other, while mutual independence (or collective independence) of events means, informally speaking, that each event is independent of any combination of other events in the collection. A similar notion exists for collections of random variables. M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proxy (statistics)
In statistics, a proxy or proxy variable is a variable that is not in itself directly relevant, but that serves in place of an unobservable or immeasurable variable. In order for a variable to be a good proxy, it must have a close correlation, not necessarily linear, with the variable of interest. This correlation might be either positive or negative. Proxy variable must relate to an unobserved variable, must correlate with disturbance, and must not correlate with regressors once the disturbance is controlled for. Examples In social sciences, proxy measurements are often required to stand in for variables that cannot be directly measured. This process of standing in is also known as operationalization. Per-capita gross domestic product (GDP) is often used as a proxy for measures of standard of living or quality of life. Montgomery ''et al.'' examine several proxies used, and point out limitations with each, stating "In poor countries, no single empirical measure can be expected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonparametric Statistics
Nonparametric statistics is a type of statistical analysis that makes minimal assumptions about the underlying distribution of the data being studied. Often these models are infinite-dimensional, rather than finite dimensional, as in parametric statistics. Nonparametric statistics can be used for descriptive statistics or statistical inference. Nonparametric tests are often used when the assumptions of parametric tests are evidently violated. Definitions The term "nonparametric statistics" has been defined imprecisely in the following two ways, among others: The first meaning of ''nonparametric'' involves techniques that do not rely on data belonging to any particular parametric family of probability distributions. These include, among others: * Methods which are ''distribution-free'', which do not rely on assumptions that the data are drawn from a given parametric family of probability distributions. * Statistics defined to be a function on a sample, without dependency on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Collection
Data collection or data gathering is the process of gathering and measuring information on targeted variables in an established system, which then enables one to answer relevant questions and evaluate outcomes. Data collection is a research component in all study fields, including physical science, physical and social sciences, humanities, and business. While methods vary by discipline, the emphasis on ensuring accurate and honest collection remains the same. The goal for all data collection is to capture evidence that allows data analysis to lead to the formulation of credible answers to the questions that have been posed. Regardless of the field of or preference for defining data (Quantitative method, quantitative or Qualitative method, qualitative), accurate data collection is essential to maintain research integrity. The selection of appropriate data collection instruments (existing, modified, or newly developed) and delineated instructions for their correct use reduce the l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |