|
Berkson Error Model
The Berkson error model is a description of random error (or misclassification) in measurement. Unlike classical error, Berkson error causes little or no bias in the measurement. It was proposed by Joseph Berkson in an article entitled “Are there two regressions?,” published in 1950. An example of Berkson error arises in exposure assessment in epidemiological studies. Berkson error may predominate over classical error in cases where exposure data are highly aggregated. While this kind of error reduces the power of a study, risk estimates themselves are not themselves attenuated (as would be the case where random error Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.Dodge, Y. (2003) ''The Oxford Dictionary of Statistical Terms'', OUP. In statistics, an error is not necessarily a "mistake" ... predominates). References Further reading * * Accuracy and precision Statistical deviation and dispersio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Error
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.Dodge, Y. (2003) ''The Oxford Dictionary of Statistical Terms'', OUP. In statistics, an error is not necessarily a " mistake". Variability is an inherent part of the results of measurements and of the measurement process. Measurement errors can be divided into two components: ''random'' and ''systematic''. Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system. Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged. Measurement errors can be summarized in terms of accuracy and precision. Measurement error should not be confused with measurement uncer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measurement
Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events. In other words, measurement is a process of determining how large or small a physical quantity is as compared to a basic reference quantity of the same kind. The scope and application of measurement are dependent on the context and discipline. In natural sciences and engineering, measurements do not apply to nominal properties of objects or events, which is consistent with the guidelines of the ''International vocabulary of metrology'' published by the International Bureau of Weights and Measures. However, in other fields such as statistics as well as the social and behavioural sciences, measurements can have multiple levels, which would include nominal, ordinal, interval and ratio scales. Measurement is a cornerstone of trade, science, technology and quantitative research in many disciplines. Historically, many measurement systems existed fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Error
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its "true value" (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the ''estimated'' value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals. In econometrics, "errors" are also called disturbances. Introduction Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors are the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joseph Berkson
Joseph Berkson (14 May 1899 – 12 September 1982) was trained as a physicist (BSc 1920 College of City of New York, M.A., 1922, Columbia), physician (M.D., 1927, Johns Hopkins), and statistician (Dr.Sc., 1928, Johns Hopkins).O'Fallon WM (1998). "Berkson, Joseph". Armitage P, Colton T, Editors-in-Chief. ''Encyclopedia of Biostatistics.'' Chichester: John Wiley & Sons. Volume 1, pp. 290-295. He is best known for having identified a source of bias in observational studies caused by selection effects known as Berkson's paradox. In 1950, as Head (1934–1964) of the Division of Biometry and Medical Statistics of the Mayo Clinic, Rochester, Minnesota, Berkson wrote a key paper entitled ''Are there two regressions?''. In this paper Berkson proposed an error model for regression analysis that contradicted the classical error model until that point assumed to generally apply and this has since been termed the Berkson error model. Whereas the classical error model is statistically independ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of The American Statistical Association
The ''Journal of the American Statistical Association (JASA)'' is the primary journal published by the American Statistical Association, the main professional body for statisticians in the United States. It is published four times a year in March, June, September and December by Taylor & Francis, Ltd on behalf of the American Statistical Association. As a statistics journal it publishes articles primarily focused on the application of statistics, statistical theory and methods in economic, social, physical, engineering, and health sciences. The journal also includes reviews of academic books which are important to the advancement of the field. It had an impact factor of 2.063 in 2010, tenth highest in the "Statistics and Probability" category of ''Journal Citation Reports''. In a 2003 survey of statisticians, the ''Journal of the American Statistical Association'' was ranked first, among all journals, for "Applications of Statistics" and second (after ''Annals of Statistics'') f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exposure Assessment
Exposure assessment is a branch of environmental science and occupational hygiene that focuses on the processes that take place at the interface between the environment containing the contaminant of interest and the organism being considered. These are the final steps in the path to release an environmental contaminant, through transport to its effect in a biological system. It tries to measure how much of a contaminant can be absorbed by an exposed target organism, in what form, at what rate and how much of the absorbed amount is actually available to produce a biological effect. Although the same general concepts apply to other organisms, the overwhelming majority of applications of exposure assessment are concerned with human health, making it an important tool in public health. Definition Exposure assessment is the process of estimating or measuring the magnitude, frequency and duration of exposure to an agent, along with the number and characteristics of the population exp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
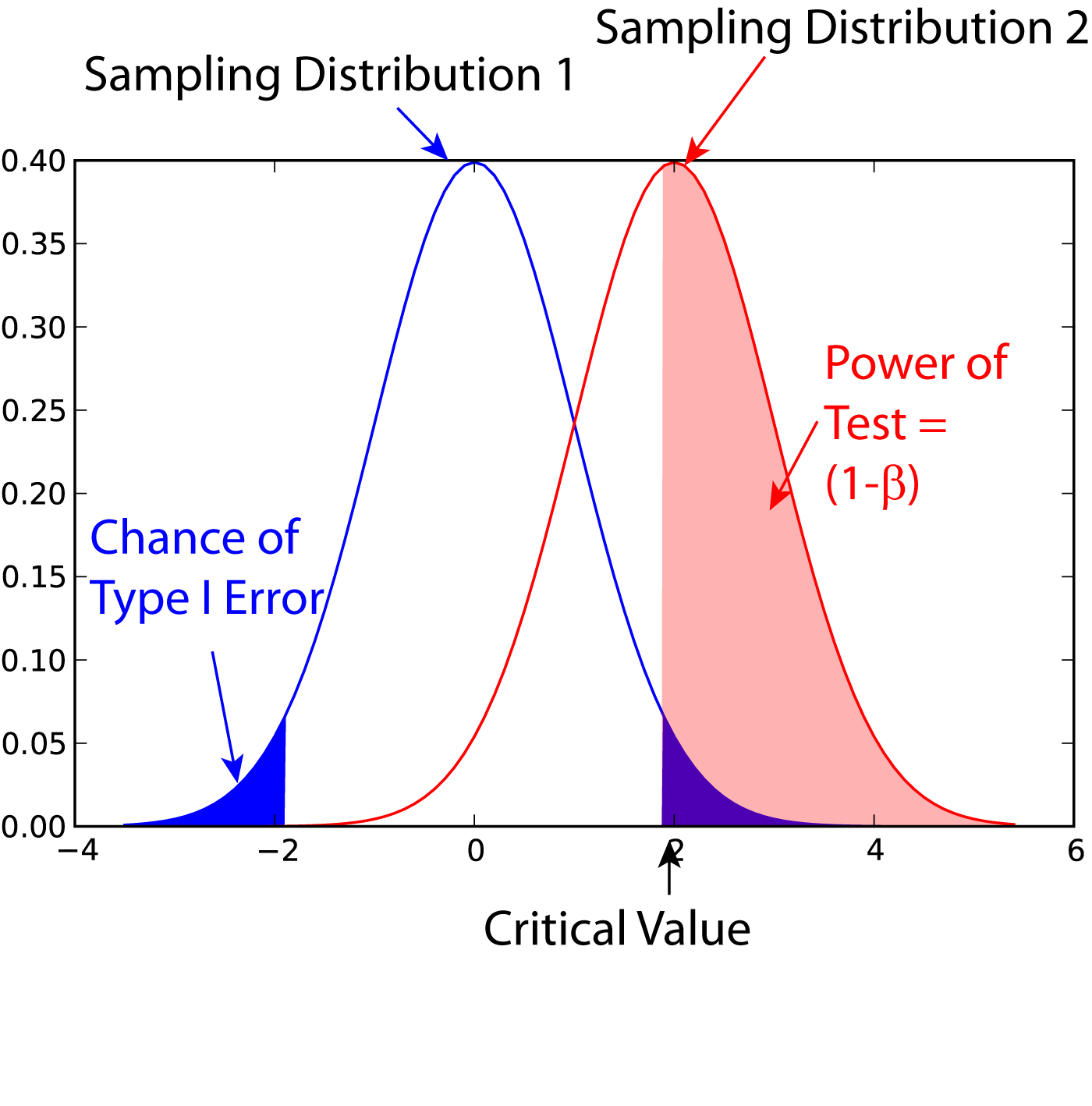
Statistical Power
In statistics, the power of a binary hypothesis test is the probability that the test correctly rejects the null hypothesis (H_0) when a specific alternative hypothesis (H_1) is true. It is commonly denoted by 1-\beta, and represents the chances of a true positive detection conditional on the actual existence of an effect to detect. Statistical power ranges from 0 to 1, and as the power of a test increases, the probability \beta of making a type II error by wrongly failing to reject the null hypothesis decreases. Notation This article uses the following notation: * ''β'' = probability of a Type II error, known as a "false negative" * 1 − ''β'' = probability of a "true positive", i.e., correctly rejecting the null hypothesis. "1 − ''β''" is also known as the power of the test. * ''α'' = probability of a Type I error, known as a "false positive" * 1 − ''α'' = probability of a "true negative", i.e., correctly not rejecting the null hypothesis Description For a ty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Accuracy And Precision
Accuracy and precision are two measures of ''observational error''. ''Accuracy'' is how close a given set of measurements ( observations or readings) are to their ''true value'', while ''precision'' is how close the measurements are to each other. In other words, ''precision'' is a description of '' random errors'', a measure of statistical variability. ''Accuracy'' has two definitions: # More commonly, it is a description of only '' systematic errors'', a measure of statistical bias of a given measure of central tendency; low accuracy causes a difference between a result and a true value; ISO calls this ''trueness''. # Alternatively, ISO defines accuracy as describing a combination of both types of observational error (random and systematic), so high accuracy requires both high precision and high trueness. In the first, more common definition of "accuracy" above, the concept is independent of "precision", so a particular set of data can be said to be accurate, precise, both, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Deviation And Dispersion
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An exp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |