|
Endogeneity (econometrics)
In econometrics, endogeneity broadly refers to situations in which an explanatory variable is correlated with the error term. The distinction between endogenous and exogenous variables originated in simultaneous equations models, where one separates variables whose values are determined by the model from variables which are predetermined. Ignoring simultaneity in the estimation leads to biased estimates as it violates the exogeneity assumption of the Gauss–Markov theorem. The problem of endogeneity is often ignored by researchers conducting non-experimental research and doing so precludes making policy recommendations. Instrumental variable techniques are commonly used to mitigate this problem. Besides simultaneity, correlation between explanatory variables and the error term can arise when an unobserved or omitted variable is confounding both independent and dependent variables, or when independent variables are measured with error. Exogeneity versus endogeneity In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Econometrics
Econometrics is an application of statistical methods to economic data in order to give empirical content to economic relationships. M. Hashem Pesaran (1987). "Econometrics", '' The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 p. 8–22 Reprinted in J. Eatwell ''et al.'', eds. (1990). ''Econometrics: The New Palgrave''p. 1 p. 1–34Abstract ( 2008 revision by J. Geweke, J. Horowitz, and H. P. Pesaran). More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference." An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships." Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today. A basic tool for econometrics is the multiple linear regression model. ''Econome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confounding
In causal inference, a confounder is a variable that influences both the dependent variable and independent variable, causing a spurious association. Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations.Pearl, J., (2009). Simpson's Paradox, Confounding, and Collapsibility In ''Causality: Models, Reasoning and Inference'' (2nd ed.). New York : Cambridge University Press. The existence of confounders is an important quantitative explanation why correlation does not imply causation. Some notations are explicitly designed to identify the existence, possible existence, or non-existence of confounders in causal relationships between elements of a system. Confounders are threats to internal validity. Example Let's assume that a trucking company owns a fleet of trucks made by two different manufacturers. Trucks made by one manufacturer are called "A Trucks" and trucks made by the other manufacturer are called "B Trucks." ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
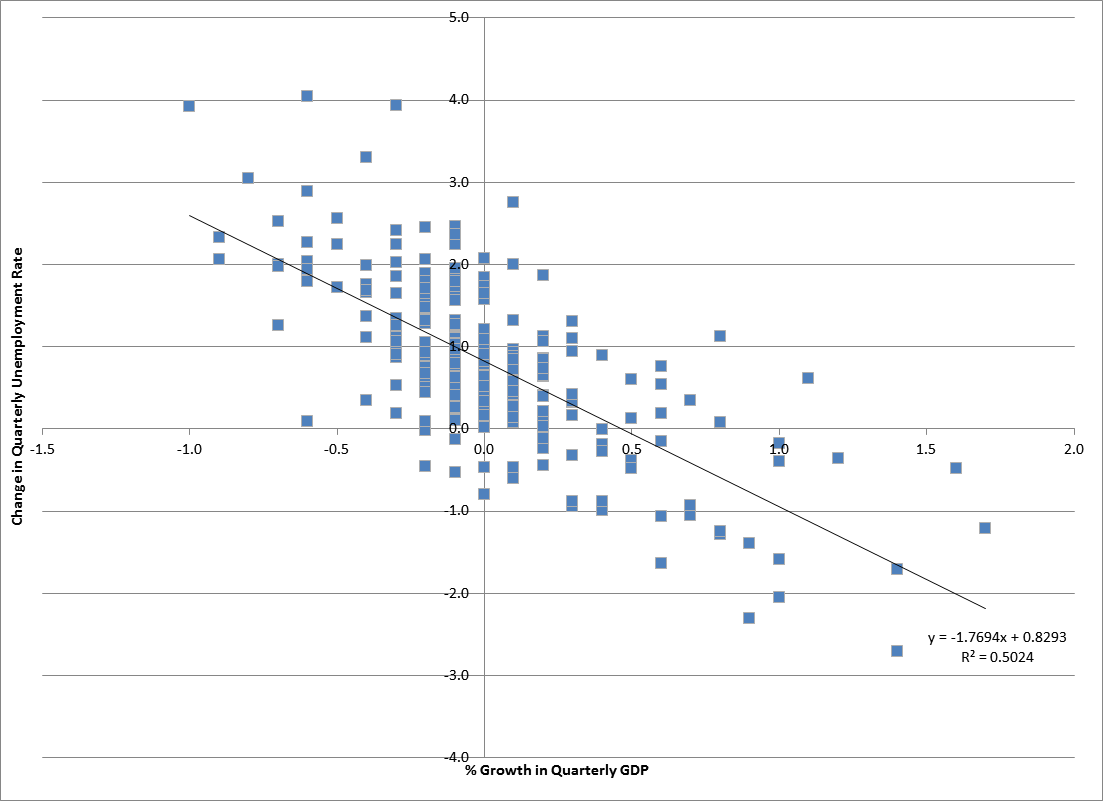
Time Series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Equation Modeling
Structural equation modeling (SEM) is a diverse set of methods used by scientists for both observational and experimental research. SEM is used mostly in the social and behavioral science fields, but it is also used in epidemiology, business, and other fields. A common definition of SEM is, "...a class of methodologies that seeks to represent hypotheses about the means, variances, and covariances of observed data in terms of a smaller number of 'structural' parameters defined by a hypothesized underlying conceptual or theoretical model,". SEM involves a model representing how various aspects of some phenomenon are thought to causally connect to one another. Structural equation models often contain postulated causal connections among some latent variables (variables thought to exist but which can't be directly observed). Additional causal connections link those latent variables to observed variables whose values appear in a data set. The causal connections are represented using ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confounding Variable
In causal inference, a confounder is a variable that influences both the dependent variable and independent variable, causing a spurious association. Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations.Pearl, J., (2009). Simpson's Paradox, Confounding, and Collapsibility In ''Causality: Models, Reasoning and Inference'' (2nd ed.). New York : Cambridge University Press. The existence of confounders is an important quantitative explanation why correlation does not imply causation. Some notations are explicitly designed to identify the existence, possible existence, or non-existence of confounders in causal relationships between elements of a system. Confounders are threats to internal validity. Example Let's assume that a trucking company owns a fleet of trucks made by two different manufacturers. Trucks made by one manufacturer are called "A Trucks" and trucks made by the other manufacturer are called "B Trucks. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heckman Correction
The Heckman correction is a statistical technique to correct bias from non-randomly selected samples or otherwise incidentally truncated dependent variables, a pervasive issue in quantitative social sciences when using observational data. Conceptually, this is achieved by explicitly modelling the individual sampling probability of each observation (the so-called selection equation) together with the conditional expectation of the dependent variable (the so-called outcome equation). The resulting likelihood function is mathematically similar to the tobit model for censored dependent variables, a connection first drawn by James Heckman in 1974. Heckman also developed a two-step control function approach to estimate this model, which avoids the computational burden of having to estimate both equations jointly, albeit at the cost of inefficiency. Heckman received the Nobel Memorial Prize in Economic Sciences in 2000 for his work in this field. Method Statistical analyses b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instrumental Variable
In statistics, econometrics, epidemiology and related disciplines, the method of instrumental variables (IV) is used to estimate causal relationships when controlled experiments are not feasible or when a treatment is not successfully delivered to every unit in a randomized experiment. Intuitively, IVs are used when an explanatory variable of interest is correlated with the error term (endogenous), in which case ordinary least squares and ANOVA give biased results. A valid instrument induces changes in the explanatory variable (is correlated with the endogenous variable) but has no independent effect on the dependent variable and is not correlated with the error term, allowing a researcher to uncover the causal effect of the explanatory variable on the dependent variable. Instrumental variable methods allow for consistent estimation when the explanatory variables (covariates) are correlated with the error terms in a regression model. Such correlation may occur when: # changes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Consistent Estimator
In statistics, a consistent estimator or asymptotically consistent estimator is an estimator—a rule for computing estimates of a parameter ''θ''0—having the property that as the number of data points used increases indefinitely, the resulting sequence of estimates converges in probability to ''θ''0. This means that the distributions of the estimates become more and more concentrated near the true value of the parameter being estimated, so that the probability of the estimator being arbitrarily close to ''θ''0 converges to one. In practice one constructs an estimator as a function of an available sample of size ''n'', and then imagines being able to keep collecting data and expanding the sample ''ad infinitum''. In this way one would obtain a sequence of estimates indexed by ''n'', and consistency is a property of what occurs as the sample size “grows to infinity”. If the sequence of estimates can be mathematically shown to converge in probability to the true value '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bias Of An Estimator
In statistics, the bias of an estimator (or bias function) is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called ''unbiased''. In statistics, "bias" is an property of an estimator. Bias is a distinct concept from consistency: consistent estimators converge in probability to the true value of the parameter, but may be biased or unbiased (see bias versus consistency for more). All else being equal, an unbiased estimator is preferable to a biased estimator, although in practice, biased estimators (with generally small bias) are frequently used. When a biased estimator is used, bounds of the bias are calculated. A biased estimator may be used for various reasons: because an unbiased estimator does not exist without further assumptions about a population; because an estimator is difficult to compute (as in unbiased estimation of standard deviation); because a biased esti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A mode ... model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Some sources consider OLS to be linear regression. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Term
In mathematics and statistics, an error term is an additive type of error. In writing, an error term is an instance of faulty language or grammar. Common examples include: * errors and residuals in statistics, e.g. in linear regression * the error term in numerical integration In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral. The term numerical quadrature (often abbreviated to quadrature) is more or less a synonym for "numerical integr ... {{sia, mathematics Error measures ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |