|
Discrete Value
In mathematics and statistics, a quantitative variable may be continuous or discrete if they are typically obtained by ''measuring'' or '' counting'', respectively. If it can take on two particular real values such that it can also take on all real values between them (even values that are arbitrarily close together), the variable is continuous in that interval. If it can take on a value such that there is a non-infinitesimal gap on each side of it containing no values that the variable can take on, then it is discrete around that value. In some contexts a variable can be discrete in some ranges of the number line and continuous in others. Continuous variable A continuous variable is a variable whose value is obtained by measuring, i.e., one which can take on an uncountable set of values. For example, a variable over a non-empty range of the real numbers is continuous, if it can take on any value in that range. The reason is that any range of real numbers between a and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Numbers
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country"). Numbers used for counting are called '' cardinal numbers'', and numbers used for ordering are called ''ordinal numbers''. Natural numbers are sometimes used as labels, known as ''nominal numbers'', having none of the properties of numbers in a mathematical sense (e.g. sports jersey numbers). Some definitions, including the standard ISO 80000-2, begin the natural numbers with , corresponding to the non-negative integers , whereas others start with , corresponding to the positive integers Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers). The natural numbers form a set. Many other number sets are built by succ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Up until the 19th century, mathematicians largely relied on intuitive notions of continuity, and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probit Regression
In statistics, a probit model is a type of regression where the dependent variable can take only two values, for example married or not married. The word is a portmanteau, coming from ''probability'' + ''unit''. The purpose of the model is to estimate the probability that an observation with particular characteristics will fall into a specific one of the categories; moreover, classifying observations based on their predicted probabilities is a type of binary classification model. A probit model is a popular specification for a binary response model. As such it treats the same set of problems as does logistic regression using similar techniques. When viewed in the generalized linear model framework, the probit model employs a probit link function. It is most often estimated using the maximum likelihood procedure, such an estimation being called a probit regression. Conceptual framework Suppose a response variable ''Y'' is ''binary'', that is it can have only two possible ou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Regression
In statistics, the logistic model (or logit model) is a statistical model that models the probability of an event taking place by having the log-odds for the event be a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regression (or logit regression) is estimation theory, estimating the parameters of a logistic model (the coefficients in the linear combination). Formally, in binary logistic regression there is a single binary variable, binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function, h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dependent Variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest (e.g. human population size) to predict future values (the dependent variable). Of the two, it is always the dependent variable whose variation is being studied, by altering inputs, also known as regressors in a statistical context. In an experiment, any variable that can be attributed a value without attributing a value to any other variable is called a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dummy Variable (statistics)
In regression analysis, a dummy variable (also known as indicator variable or just dummy) is one that takes the values 0 or 1 to indicate the absence or presence of some categorical effect that may be expected to shift the outcome. For example, if we were studying the relationship between gender and income, we could use a dummy variable to represent the gender of each individual in the study. The variable would take on a value of 1 for males and 0 for females. Dummy variables are commonly used in regression analysis to represent categorical variables that have more than two levels, such as education level or occupation. In this case, multiple dummy variables would be created to represent each level of the variable, and only one dummy variable would take on a value of 1 for each observation. Dummy variables are useful because they allow us to include categorical variables in our analysis, which would otherwise be difficult to include due to their non-numeric nature. They can also h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empirical
Empirical evidence for a proposition is evidence, i.e. what supports or counters this proposition, that is constituted by or accessible to sense experience or experimental procedure. Empirical evidence is of central importance to the sciences and plays a role in various other fields, like epistemology and law. There is no general agreement on how the terms ''evidence'' and ''empirical'' are to be defined. Often different fields work with quite different conceptions. In epistemology, evidence is what justifies beliefs or what determines whether holding a certain belief is rational. This is only possible if the evidence is possessed by the person, which has prompted various epistemologists to conceive evidence as private mental states like experiences or other beliefs. In philosophy of science, on the other hand, evidence is understood as that which '' confirms'' or ''disconfirms'' scientific hypotheses and arbitrates between competing theories. For this role, it is important that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
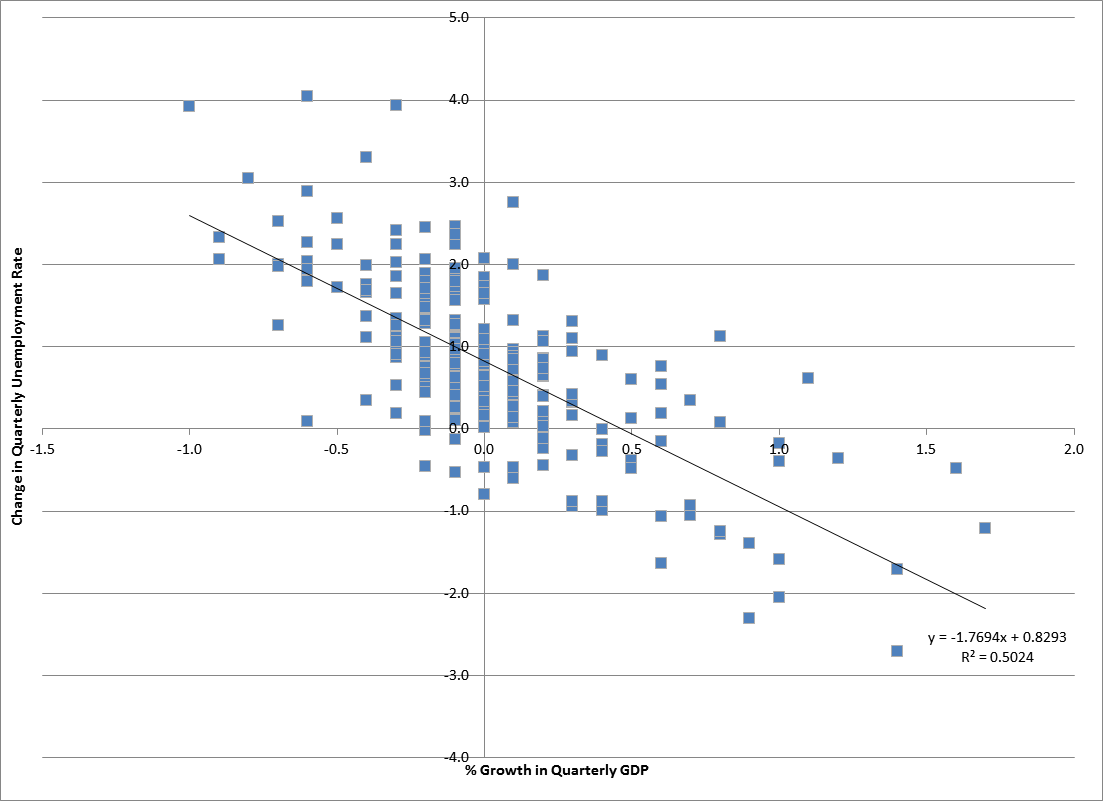
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Econometrics
Econometrics is the application of statistical methods to economic data in order to give empirical content to economic relationships.M. Hashem Pesaran (1987). "Econometrics," '' The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 p. 8–22 Reprinted in J. Eatwell ''et al.'', eds. (1990). ''Econometrics: The New Palgrave''p. 1p. 1–34Abstract (2008 revision by J. Geweke, J. Horowitz, and H. P. Pesaran). More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference". An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships". Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today. A basic tool for econometrics is the multiple linear regression model. ''Econometric the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Difference Equation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Time
In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which variables that evolve over time are modeled. Discrete time Discrete time views values of variables as occurring at distinct, separate "points in time", or equivalently as being unchanged throughout each non-zero region of time ("time period")—that is, time is viewed as a discrete variable. Thus a non-time variable jumps from one value to another as time moves from one time period to the next. This view of time corresponds to a digital clock that gives a fixed reading of 10:37 for a while, and then jumps to a new fixed reading of 10:38, etc. In this framework, each variable of interest is measured once at each time period. The number of measurements between any two time periods is finite. Measurements are typically made at sequential integer values of the variable "time". A discrete signal or discrete-time signal is a time series consisting of a sequence of quantit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |