Dictionary Learning

picture info	Dictionary Learning Sparse dictionary learning (also known as sparse coding or SDL) is a representation learning method which aims to find a sparse representation of the input data in the form of a linear combination of basic elements as well as those basic elements themselves. These elements are called ''atoms'', and they compose a ''dictionary''. Atoms in the dictionary are not required to be orthogonal, and they may be an over-complete spanning set. This problem setup also allows the dimensionality of the signals being represented to be higher than any one of the signals being observed. These two properties lead to having seemingly redundant atoms that allow multiple representations of the same signal, but also provide an improvement in sparsity and flexibility of the representation. One of the most important applications of sparse dictionary learning is in the field of compressed sensing or signal recovery. In compressed sensing, a high-dimensional signal can be recovered with only a few linear me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
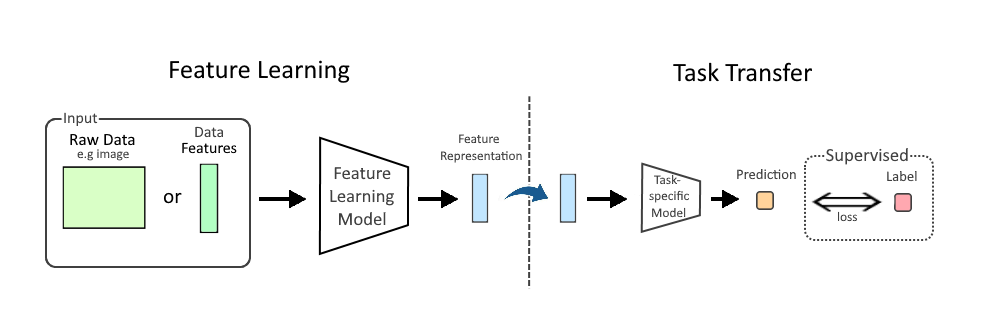
picture info	Representation Learning In machine learning (ML), feature learning or representation learning is a set of techniques that allow a system to automatically discover the representations needed for feature detection or classification from raw data. This replaces manual feature engineering and allows a machine to both learn the features and use them to perform a specific task. Feature learning is motivated by the fact that ML tasks such as classification often require input that is mathematically and computationally convenient to process. However, real-world data, such as image, video, and sensor data, have not yielded to attempts to algorithmically define specific features. An alternative is to discover such features or representations through examination, without relying on explicit algorithms. Feature learning can be either supervised, unsupervised, or self-supervised: * In supervised feature learning, features are learned using labeled input data. Labeled data includes input-label pairs where the inp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Audio Signal Processing Audio signal processing is a subfield of signal processing that is concerned with the electronic manipulation of audio signals. Audio signals are electronic representations of sound waves—longitudinal waves which travel through air, consisting of compressions and rarefactions. The energy contained in audio signals or sound power level is typically measured in decibels. As audio signals may be represented in either Digital signal (signal processing), digital or analog signal, analog format, processing may occur in either domain. Analog processors operate directly on the electrical signal, while digital processors operate mathematically on its digital representation. History The motivation for audio signal processing began at the beginning of the 20th century with inventions like the telephone, phonograph, and radio that allowed for the transmission and storage of audio signals. Audio processing was necessary for early radio broadcasting, as there were many problems with stud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Frobenius Norm In the field of mathematics, norms are defined for elements within a vector space. Specifically, when the vector space comprises matrices, such norms are referred to as matrix norms. Matrix norms differ from vector norms in that they must also interact with matrix multiplication. Preliminaries Given a field \ K\ of either real or complex numbers (or any complete subset thereof), let \ K^\ be the -vector space of matrices with m rows and n columns and entries in the field \ K ~. A matrix norm is a norm on \ K^~. Norms are often expressed with double vertical bars (like so: \ \, A\, \ ). Thus, the matrix norm is a function \ \, \cdot\, : K^ \to \R^\ that must satisfy the following properties: For all scalars \ \alpha \in K\ and matrices \ A, B \in K^\ , * \, A\, \ge 0\ (''positive-valued'') * \, A\, = 0 \iff A=0_ (''definite'') * \left\, \alpha\ A \right\, = \left, \alpha \\ \left\, A\right\, \ (''absolutely homogeneous'') * \, A + B \, \le \, A \, + \, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Lasso (statistics) In statistics and machine learning, lasso (least absolute shrinkage and selection operator; also Lasso, LASSO or L1 regularization) is a regression analysis method that performs both variable selection and Regularization (mathematics), regularization in order to enhance the prediction accuracy and interpretability of the resulting statistical model. The lasso method assumes that the coefficients of the linear model are sparse, meaning that few of them are non-zero. It was originally introduced in geophysics, and later by Robert Tibshirani, who coined the term. Lasso was originally formulated for linear regression models. This simple case reveals a substantial amount about the estimator. These include its relationship to ridge regression and best subset selection and the connections between lasso coefficient estimates and so-called soft thresholding. It also reveals that (like standard linear regression) the coefficient estimates do not need to be unique if covariates are collinear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
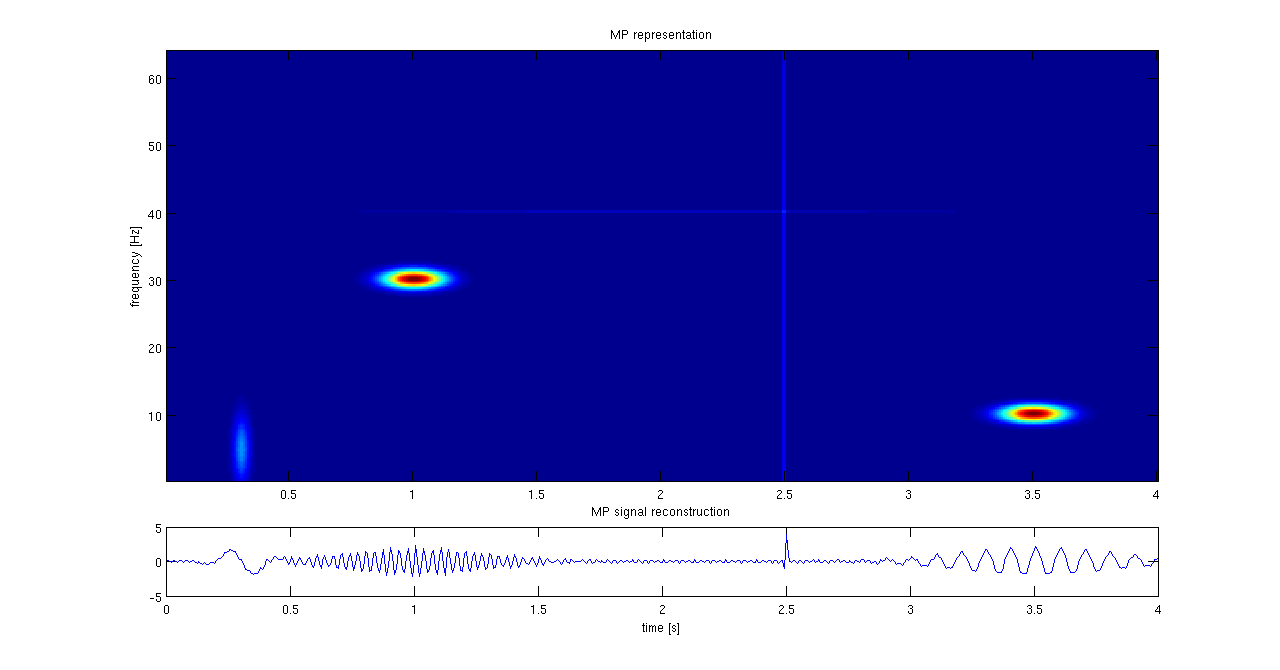
picture info	Matching Pursuit Matching pursuit (MP) is a sparse approximation algorithm which finds the "best matching" projections of multidimensional data onto the span of an over-complete (i.e., redundant) dictionary D. The basic idea is to approximately represent a signal f from Hilbert space H as a weighted sum of finitely many functions g_ (called atoms) taken from D. An approximation with N atoms has the form : f(t) \approx \hat f_N(t) := \sum_^ a_n g_(t) where g_ is the \gamma_nth column of the matrix D and a_n is the scalar weighting factor (amplitude) for the atom g_. Normally, not every atom in D will be used in this sum. Instead, matching pursuit chooses the atoms one at a time in order to maximally (greedily) reduce the approximation error. This is achieved by finding the atom that has the highest inner product with the signal (assuming the atoms are normalized), subtracting from the signal an approximation that uses only that one atom, and repeating the process until the signal is satisfactoril ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Sparse Approximation Sparse approximation (also known as sparse representation) theory deals with sparse solutions for systems of linear equations. Techniques for finding these solutions and exploiting them in applications have found wide use in image processing, signal processing, machine learning, medical imaging, and more. Sparse decomposition Noiseless observations Consider a linear system of equations x = D\alpha, where D is an underdetermined m\times p matrix (m < p) and $x \in \mathbb^m,\alpha \in \mathbb^p$ . The matrix $D$ (typically assumed to be full-rank) is referred to as the dictionary, and $x$ is a signal of interest. The core sparse representation problem is defined as the quest for the sparsest possible representation $\alpha$ satisfying $x = D\alpha$ . Due to the underdetermined nature of $D$ , this linear system admits in general infinitely many possible solutions, and among these we seek the one with the fewe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Basis (linear Algebra) In mathematics, a Set (mathematics), set of elements of a vector space is called a basis (: bases) if every element of can be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to . The elements of a basis are called . Equivalently, a set is a basis if its elements are linearly independent and every element of is a linear combination of elements of . In other words, a basis is a linearly independent spanning set. A vector space can have several bases; however all the bases have the same number of elements, called the dimension (vector space), dimension of the vector space. This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces. Basis vectors find applications in the study of crystal structures and frame of reference, frames of reference. De ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Principal Component Analysis Principal component analysis (PCA) is a linear dimensionality reduction technique with applications in exploratory data analysis, visualization and data preprocessing. The data is linearly transformed onto a new coordinate system such that the directions (principal components) capturing the largest variation in the data can be easily identified. The principal components of a collection of points in a real coordinate space are a sequence of p unit vectors, where the i-th vector is the direction of a line that best fits the data while being orthogonal to the first i-1 vectors. Here, a best-fitting line is defined as one that minimizes the average squared perpendicular distance from the points to the line. These directions (i.e., principal components) constitute an orthonormal basis in which different individual dimensions of the data are linearly uncorrelated. Many studies use the first two principal components in order to plot the data in two dimensions and to visually identi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Dimensionality Reduction Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable. Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Linear approaches can be further divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an intermediate step to facilitat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
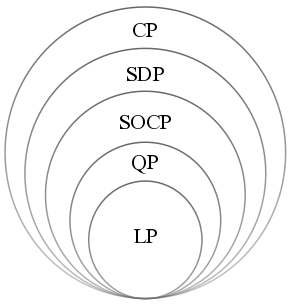
picture info	Convex Optimization Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard. Definition Abstract form A convex optimization problem is defined by two ingredients: * The ''objective function'', which is a real-valued convex function of ''n'' variables, f :\mathcal D \subseteq \mathbb^n \to \mathbb; * The ''feasible set'', which is a convex subset C\subseteq \mathbb^n. The goal of the problem is to find some \mathbf \in C attaining :\inf \. In general, there are three options regarding the existence of a solution: * If such a point ''x''* exists, it is referred to as an ''optimal point'' or ''solution''; the set of all optimal points is called the ''optimal set''; and the problem is called ''solvable''. * If f is unbou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	L1-norm In mathematics, the spaces are function spaces defined using a natural generalization of the Norm (mathematics)#p-norm, -norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue , although according to the Nicolas Bourbaki, Bourbaki group they were first introduced by Frigyes Riesz . spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical analysis of measure and probability spaces, Lebesgue spaces are used also in the theoretical discussion of problems in physics, statistics, economics, finance, engineering, and other disciplines. Preliminaries The -norm in finite dimensions The Euclidean length of a vector x = (x_1, x_2, \dots, x_n) in the n-dimensional real number, real vector space \Reals^n is given by the Euclidean norm: \, x\, _2 = \left(^2 + ^2 + \dotsb + ^2\right)^. The Euclidean distance between two points x and y is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	L0 Norm In mathematics, the spaces are function spaces defined using a natural generalization of the -norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue , although according to the Bourbaki group they were first introduced by Frigyes Riesz . spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical analysis of measure and probability spaces, Lebesgue spaces are used also in the theoretical discussion of problems in physics, statistics, economics, finance, engineering, and other disciplines. Preliminaries The -norm in finite dimensions The Euclidean length of a vector x = (x_1, x_2, \dots, x_n) in the n-dimensional real vector space \Reals^n is given by the Euclidean norm: \, x\, _2 = \left(^2 + ^2 + \dotsb + ^2\right)^. The Euclidean distance between two points x and y is the length \, x - y\, _2 of the straight line between th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]