|
Degrees (angle)
A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of a plane angle in which one full rotation is 360 degrees. It is not an SI unit—the SI unit of angular measure is the radian—but it is mentioned in the SI brochure as an accepted unit. Because a full rotation equals 2 radians, one degree is equivalent to radians. History The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the sun, which follows through the ecliptic path over the course of the year, seems to advance in its path by approximately one degree each day. Some ancient calendars, such as the Persian calendar and the Babylonian calendar, used 360 days for a year. The use of a calendar with 360 days may be related to the use of sexagesimal numbers. Anoth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. The term is a calque of Latin ''angulus rectus''; here ''rectus'' means "upright", referring to the vertical perpendicular to a horizontal base line. Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to Euclidean vector, vectors. The presence of a right angle in a triangle is the defining factor for right triangles, making the right angle basic to trigonometry. Etymology The meaning of ''right'' in ''right angle'' possibly refers to the Classical Latin, Latin adjective ''rectus'' 'erect, straight, upright, perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
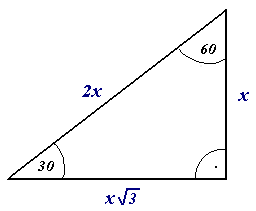
Equilateral Chord With Length Equal To Radius
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle. Principal properties Denoting the common length of the sides of the equilateral triangle as a, we can determine using the Pythagorean theorem that: *The area is A=\frac a^2, *The perimeter is p=3a\,\! *The radius of the circumscribed circle is R = \frac *The radius of the inscribed circle is r=\frac a or r=\frac *The geometric center of the triangle is the center of the circumscribed and inscribed circles *The altitude (height) from any side is h=\frac a Denoting the radius of the circumscribed circle as ''R'', we can determine using trigonometry that: *The area of the triangle is \mathrm=\fracR^2 Many of these quantities have simple re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
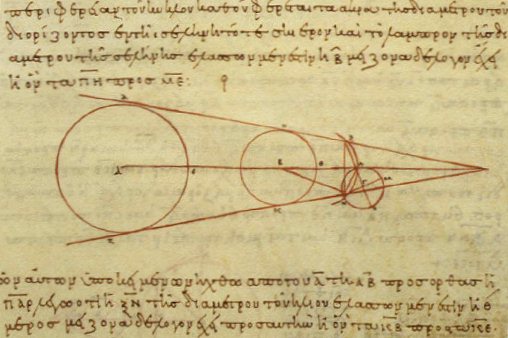
Aristarchus Of Samos
Aristarchus of Samos (; grc-gre, Ἀρίσταρχος ὁ Σάμιος, ''Aristarkhos ho Samios''; ) was an ancient Greek astronomer An astronomer is a scientist in the field of astronomy who focuses their studies on a specific question or field outside the scope of Earth. They observe astronomical objects such as stars, planets, natural satellite, moons, comets and galaxy, g ... and mathematician who presented the first known Heliocentrism, heliocentric model that placed the Sun at the center of the known universe, with the Earth revolving around the Sun once a year and rotating about its axis once a day. He was a student of Strato of Lampsacus, who was the third head of the Peripatetic school, Peripatetic School in Ancient Greece, Greece. According to Ptolemy, during Aristarchus' time there, he observed the summer solstice of 280 BCE. Along with his contributions to the heliocentric model, as reported by Vitruvius, he created two separate sundials: one that is a flat dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chord (geometry)
A chord of a circle is a straight line segment whose endpoints both lie on a circular arc. The infinite line extension of a chord is a secant line, or just ''secant''. More generally, a chord is a line segment joining two points on any curve, for instance, an ellipse. A chord that passes through a circle's center point is the circle's diameter. The word ''chord'' is from the Latin ''chorda'' meaning '' bowstring''. In circles Among properties of chords of a circle are the following: # Chords are equidistant from the center if and only if their lengths are equal. # Equal chords are subtended by equal angles from the center of the circle. # A chord that passes through the center of a circle is called a diameter and is the longest chord of that specific circle. # If the line extensions (secant lines) of chords AB and CD intersect at a point P, then their lengths satisfy AP·PB = CP·PD (power of a point theorem). In conics The midpoints of a set of parallel chords of a coni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greek Astronomy
Greek astronomy is astronomy written in the Greek language in classical antiquity. Greek astronomy is understood to include the Ancient Greek, Hellenistic, Greco-Roman, and Late Antiquity eras. It is not limited geographically to Greece or to ethnic Greeks, as the Greek language had become the language of scholarship throughout the Hellenistic world following the conquests of Alexander. This phase of Greek astronomy is also known as Hellenistic astronomy, while the pre-Hellenistic phase is known as Classical Greek astronomy. During the Hellenistic and Roman periods, much of the Greek and non-Greek astronomers working in the Greek tradition studied at the Museum and the Library of Alexandria in Ptolemaic Egypt. The development of astronomy by the Greek and notably Hellenistic astronomers is considered to be a major phase in the history of astronomy. Greek astronomy is characterized by seeking a geometrical model for celestial phenomena. Most of the names of the stars, planets, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Babylonian Astronomy
Babylonian astronomy was the study or recording of celestial objects during the early history of Mesopotamia. Babylonian astronomy seemed to have focused on a select group of stars and constellations known as Ziqpu stars. These constellations may have been collected from various earlier sources. The earliest catalogue, ''Three Stars Each'', mentions stars of the Akkadian Empire, of Amurru, of Elam and others. A numbering system based on sixty was used, a sexagesimal system. This system simplified the calculating and recording of unusually great and small numbers. The modern practices of dividing a circle into 360 degrees, of 60 minutes each, began with the Sumerians. During the 8th and 7th centuries BC, Babylonian astronomers developed a new empirical approach to astronomy. They began studying and recording their belief system and philosophies dealing with an ideal nature of the universe and began employing an internal logic within their predictive planetary systems. This was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
History Of Trigonometry
Early study of triangles can be traced to the 2nd millennium BC, in Egyptian mathematics ( Rhind Mathematical Papyrus) and Babylonian mathematics. Trigonometry was also prevalent in Kushite mathematics. Systematic study of trigonometric functions began in Hellenistic mathematics, reaching India as part of Hellenistic astronomy. In Indian astronomy, the study of trigonometric functions flourished in the Gupta period, especially due to Aryabhata (sixth century CE), who discovered the sine function. During the Middle Ages, the study of trigonometry continued in Islamic mathematics, by mathematicians such as Al-Khwarizmi and Abu al-Wafa. It became an independent discipline in the Islamic world, where all six trigonometric functions were known. Translations of Arabic and Greek texts led to trigonometry being adopted as a subject in the Latin West beginning in the Renaissance with Regiomontanus. The development of modern trigonometry shifted during the western Age of Enlightenment, beg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press A university press is an academic publishing house specializing in monographs and scholarly journals. Most are nonprofit organizations and an integral component of a large research university. They publish work that has been reviewed by schola ... in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilateral Triangle
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle. Principal properties Denoting the common length of the sides of the equilateral triangle as a, we can determine using the Pythagorean theorem that: *The area is A=\frac a^2, *The perimeter is p=3a\,\! *The radius of the circumscribed circle is R = \frac *The radius of the inscribed circle is r=\frac a or r=\frac *The geometric center of the triangle is the center of the circumscribed and inscribed circles *The altitude (height) from any side is h=\frac a Denoting the radius of the circumscribed circle as ''R'', we can determine using trigonometry that: *The area of the triangle is \mathrm=\fracR^2 Many of these quantities have simple r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sexagesimal
Sexagesimal, also known as base 60 or sexagenary, is a numeral system with sixty as its base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified form—for measuring time, angles, and geographic coordinates. The number 60, a superior highly composite number, has twelve factors, namely 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60, of which 2, 3, and 5 are prime numbers. With so many factors, many fractions involving sexagesimal numbers are simplified. For example, one hour can be divided evenly into sections of 30 minutes, 20 minutes, 15 minutes, 12 minutes, 10 minutes, 6 minutes, 5 minutes, 4 minutes, 3 minutes, 2 minutes, and 1 minute. 60 is the smallest number that is divisible by every number from 1 to 6; that is, it is the lowest common multiple of 1, 2, 3, 4, 5, and 6. ''In this article, all sexagesimal digits are represented as decimal numbers, except where otherwise noted. For e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Babylonian Calendar
The Babylonian calendar was a lunisolar calendar with years consisting of 12 lunar months, each beginning when a new crescent moon was first sighted low on the western horizon at sunset, plus an intercalary month inserted as needed by decree. The calendar is based on a Sumerian (Third Dynasty of Ur) predecessor preserved in the Umma calendar of Shulgi (c. 21st century BC). Months The year begins in spring, and is divided into ''reš šatti'' "beginning", ''mišil šatti'' "middle", and ''qīt šatti'' "end of the year". The word for "month" was ''arḫu'' (construct state ''araḫ''). The chief deity of the Assyrians is assigned the surplus intercalary month, showing that the calendar originates in Babylonian, and not later Assyrian times. During the 6th century BC Babylonian captivity of the Jews, the Babylonian month names were adopted into the Hebrew calendar. In Iraq and the Levant the Gregorian solar calendar is used with these names replacing the Latin ones as Arabic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iranian Calendar
The Iranian calendars or Iranian chronology ( fa, گاهشماری ایرانی, ) are a succession of calendars invented or used for over two millennia in Iran, also known as Persia. One of the longest chronological records in human history, the Iranian calendar has been modified time and again during its history to suit administrative, climatic, and religious purposes. The most influential person in laying the frameworks for the calendar and its precision was the 11th century Persian polymath, hakim Omar Khayyam. The modern Iranian calendar is currently the official civil calendar in Iran and Afghanistan. The Iranian new year begins at the midnight nearest to the instant of the northern spring equinox, as determined by astronomic calculations for the meridian (52.5°E). It is, therefore, an observation-based calendar, unlike the Gregorian, which is rule-based. This equinox occurs on or about 20 March of the Gregorian calendar. The time zone of Iran is Iran Standard Time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |