|
Document-term Matrix
A document-term matrix is a mathematical Matrix (mathematics), matrix that describes the frequency of terms that occur in each document in a collection. In a document-term matrix, rows correspond to documents in the collection and columns correspond to terms. This matrix is a specific instance of a document-feature matrix where "features" may refer to other properties of a document besides terms. It is also common to encounter the transpose, or term-document matrix where documents are the columns and terms are the rows. They are useful in the field of natural language processing and computational text analysis. While the value of the cells is commonly the raw count of a given term, there are various schemes for weighting the raw counts such as row normalizing (i.e. relative frequency/proportions) and tf-idf. Terms are commonly single words separated by whitespace or punctuation on either side (a.k.a. unigrams). In such a case, this is also referred to as "bag of words" representat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (: matrices) is a rectangle, rectangular array or table of numbers, symbol (formal), symbols, or expression (mathematics), expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotation (mathematics), rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latent Semantic Analysis
Latent semantic analysis (LSA) is a technique in natural language processing, in particular distributional semantics, of analyzing relationships between a set of documents and the terms they contain by producing a set of concepts related to the documents and terms. LSA assumes that words that are close in meaning will occur in similar pieces of text (the distributional hypothesis). A matrix containing word counts per document (rows represent unique words and columns represent each document) is constructed from a large piece of text and a mathematical technique called singular value decomposition (SVD) is used to reduce the number of rows while preserving the similarity structure among columns. Documents are then compared by cosine similarity between any two columns. Values close to 1 represent very similar documents while values close to 0 represent very dissimilar documents. An information retrieval technique using latent semantic structure was patented in 1988 by Scott D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-negative Matrix Factorization
Non-negative matrix factorization (NMF or NNMF), also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra where a matrix is factorized into (usually) two matrices and , with the property that all three matrices have no negative elements. This non-negativity makes the resulting matrices easier to inspect. Also, in applications such as processing of audio spectrograms or muscular activity, non-negativity is inherent to the data being considered. Since the problem is not exactly solvable in general, it is commonly approximated numerically. NMF finds applications in such fields as astronomy, computer vision, document clustering, missing data imputation, chemometrics, audio signal processing, recommender systems, and bioinformatics. History In chemometrics non-negative matrix factorization has a long history under the name "self modeling curve resolution". In this framework the vectors in the right matrix are continuous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
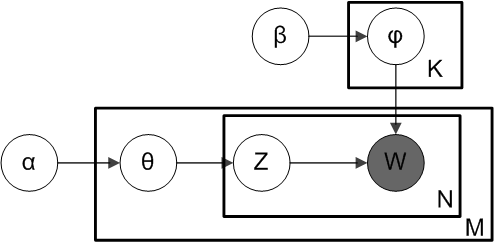
Latent Dirichlet Allocation
In natural language processing, latent Dirichlet allocation (LDA) is a Bayesian network (and, therefore, a generative statistical model) for modeling automatically extracted topics in textual corpora. The LDA is an example of a Bayesian topic model. In this, observations (e.g., words) are collected into documents, and each word's presence is attributable to one of the document's topics. Each document will contain a small number of topics. History In the context of population genetics, LDA was proposed by J. K. Pritchard, M. Stephens and P. Donnelly in 2000. LDA was applied in machine learning by David Blei, Andrew Ng and Michael I. Jordan in 2003. Overview Population genetics In population genetics, the model is used to detect the presence of structured genetic variation in a group of individuals. The model assumes that alleles carried by individuals under study have origin in various extant or past populations. The model and various inference algorithms allow sci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probabilistic Latent Semantic Analysis
Probabilistic latent semantic analysis (PLSA), also known as probabilistic latent semantic indexing (PLSI, especially in information retrieval circles) is a statistical technique for the analysis of two-mode and co-occurrence data. In effect, one can derive a low-dimensional representation of the observed variables in terms of their affinity to certain hidden variables, just as in latent semantic analysis, from which PLSA evolved. Compared to standard latent semantic analysis which stems from linear algebra and downsizes the occurrence tables (usually via a singular value decomposition), probabilistic latent semantic analysis is based on a mixture decomposition derived from a latent class model. Model Considering observations in the form of co-occurrences (w,d) of words and documents, PLSA models the probability of each co-occurrence as a mixture of conditionally independent multinomial distributions: : P(w,d) = \sum_c P(c) P(d, c) P(w, c) = P(d) \sum_c P(c, d) P(w, c) with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Clustering
Cluster analysis or clustering is the data analyzing technique in which task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some specific sense defined by the analyst) to each other than to those in other groups (clusters). It is a main task of exploratory data analysis, and a common technique for statistical data analysis, used in many fields, including pattern recognition, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Cluster analysis refers to a family of algorithms and tasks rather than one specific algorithm. It can be achieved by various algorithms that differ significantly in their understanding of what constitutes a cluster and how to efficiently find them. Popular notions of clusters include groups with small distances between cluster members, dense areas of the data space, intervals or particular statistical distributions. Clustering ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latent Semantic Analysis
Latent semantic analysis (LSA) is a technique in natural language processing, in particular distributional semantics, of analyzing relationships between a set of documents and the terms they contain by producing a set of concepts related to the documents and terms. LSA assumes that words that are close in meaning will occur in similar pieces of text (the distributional hypothesis). A matrix containing word counts per document (rows represent unique words and columns represent each document) is constructed from a large piece of text and a mathematical technique called singular value decomposition (SVD) is used to reduce the number of rows while preserving the similarity structure among columns. Documents are then compared by cosine similarity between any two columns. Values close to 1 represent very similar documents while values close to 0 represent very dissimilar documents. An information retrieval technique using latent semantic structure was patented in 1988 by Scott D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Analysis
Multivariate statistics is a subdivision of statistics encompassing the simultaneous observation and analysis of more than one outcome variable, i.e., '' multivariate random variables''. Multivariate statistics concerns understanding the different aims and background of each of the different forms of multivariate analysis, and how they relate to each other. The practical application of multivariate statistics to a particular problem may involve several types of univariate and multivariate analyses in order to understand the relationships between variables and their relevance to the problem being studied. In addition, multivariate statistics is concerned with multivariate probability distributions, in terms of both :*how these can be used to represent the distributions of observed data; :*how they can be used as part of statistical inference, particularly where several different quantities are of interest to the same analysis. Certain types of problems involving multivariate da ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trie
In computer science, a trie (, ), also known as a digital tree or prefix tree, is a specialized search tree data structure used to store and retrieve strings from a dictionary or set. Unlike a binary search tree, nodes in a trie do not store their associated key. Instead, each node's ''position'' within the trie determines its associated key, with the connections between nodes defined by individual Character (computing), characters rather than the entire key. Tries are particularly effective for tasks such as autocomplete, spell checking, and IP routing, offering advantages over hash tables due to their prefix-based organization and lack of hash collisions. Every child node shares a common prefix (computer science), prefix with its parent node, and the root node represents the empty string. While basic trie implementations can be memory-intensive, various optimization techniques such as compression and bitwise representations have been developed to improve their efficiency. A n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Synonym
A synonym is a word, morpheme, or phrase that means precisely or nearly the same as another word, morpheme, or phrase in a given language. For example, in the English language, the words ''begin'', ''start'', ''commence'', and ''initiate'' are all synonyms of one another: they are ''synonymous''. The standard test for synonymy is substitution: one form can be replaced by another in a sentence without changing its meaning. Words may often be synonymous in only one particular sense: for example, ''long'' and ''extended'' in the context ''long time'' or ''extended time'' are synonymous, but ''long'' cannot be used in the phrase ''extended family''. Synonyms with exactly the same meaning share a seme or denotational sememe, whereas those with inexactly similar meanings share a broader denotational or connotational sememe and thus overlap within a semantic field. The former are sometimes called cognitive synonyms and the latter, near-synonyms, plesionyms or poecilonyms. Lexic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polysemy
Polysemy ( or ; ) is the capacity for a Sign (semiotics), sign (e.g. a symbol, morpheme, word, or phrase) to have multiple related meanings. For example, a word can have several word senses. Polysemy is distinct from ''monosemy'', where a word has a single meaning. Polysemy is distinct from homonymy—or homophone, homophony—which is an Accident (philosophy), accidental similarity between two or more words (such as ''bear'' the animal, and the verb wikt:bear#Etymology 2, ''bear''); whereas homonymy is a mere linguistic coincidence, polysemy is not. In discerning whether a given set of meanings represent polysemy or homonymy, it is often necessary to look at the history of the word to see whether the two meanings are historically related. Lexicography, Dictionary writers often list polysemes (words or phrases with different, but related, senses) in the same entry (that is, under the same headword) and enter homonyms as separate headwords (usually with a numbering convention such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Word-sense Disambiguation
Word-sense disambiguation is the process of identifying which sense of a word is meant in a sentence or other segment of context. In human language processing and cognition, it is usually subconscious. Given that natural language requires reflection of neurological reality, as shaped by the abilities provided by the brain's neural networks, computer science has had a long-term challenge in developing the ability in computers to do natural language processing and machine learning. Many techniques have been researched, including dictionary-based methods that use the knowledge encoded in lexical resources, supervised machine learning methods in which a classifier is trained for each distinct word on a corpus of manually sense-annotated examples, and completely unsupervised methods that cluster occurrences of words, thereby inducing word senses. Among these, supervised learning approaches have been the most successful algorithms to date. Accuracy of current algorithms is diffi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |