|
Directional-change Intrinsic Time
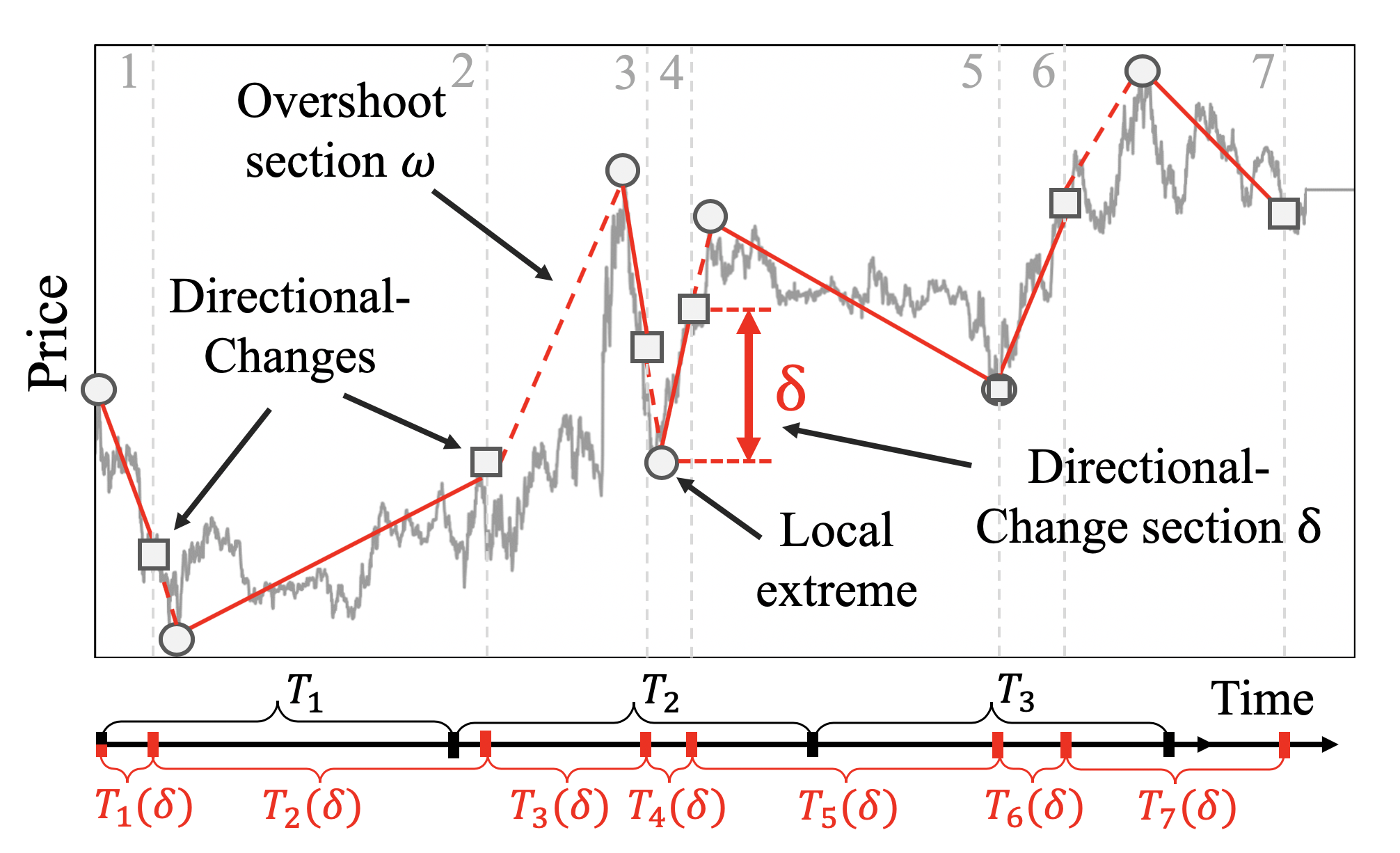
Directional-change intrinsic time is an event-based operator to dissect a data series into a sequence of alternating trends of defined size \delta. The directional-change intrinsic time operator was developed for the analysis of financial market data series. It is an alternative methodology to the concept of continuous time. Directional-change intrinsic time operator dissects a data series into a set of drawups and drawdowns or up and down trends that alternate with each other. An established trend comes to an end as soon as a trend reversal is observed. A price move that extends a trend is called overshoot and leads to new price extremes. Figure 1 provides an example of a price curve dissected by the directional change intrinsic time operator. The frequency of directional-change intrinsic events maps (1) the volatility of price changes conditional to (2) the selected threshold \delta. The stochastic nature of the underlying process is mirrored in the non-equal number of intr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overshoot (signal)
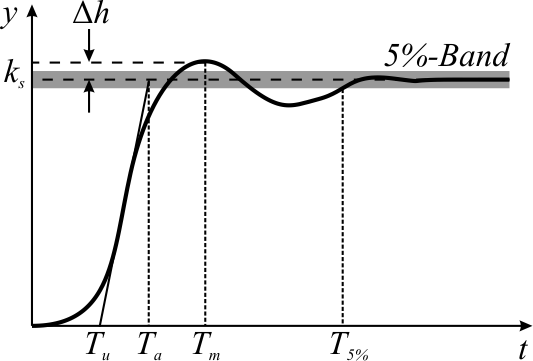
In signal processing, control theory, electronics, and mathematics, overshoot is the occurrence of a signal or function exceeding its target. Undershoot is the same phenomenon in the opposite direction. It arises especially in the step response of bandlimited systems such as low-pass filters. It is often followed by ringing, and at times conflated with the latter. Definition Maximum overshoot is defined in Katsuhiko Ogata's ''Discrete-time control systems'' as "the maximum peak value of the response curve measured from the desired response of the system." Control theory In control theory, overshoot refers to an output exceeding its final, steady-state value. For a step input, the ''percentage overshoot'' (PO) is the maximum value minus the step value divided by the step value. In the case of the unit step, the ''overshoot'' is just the maximum value of the step response minus one. Also see the definition of ''overshoot'' in an electronics context. For second-order sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volatility (finance)
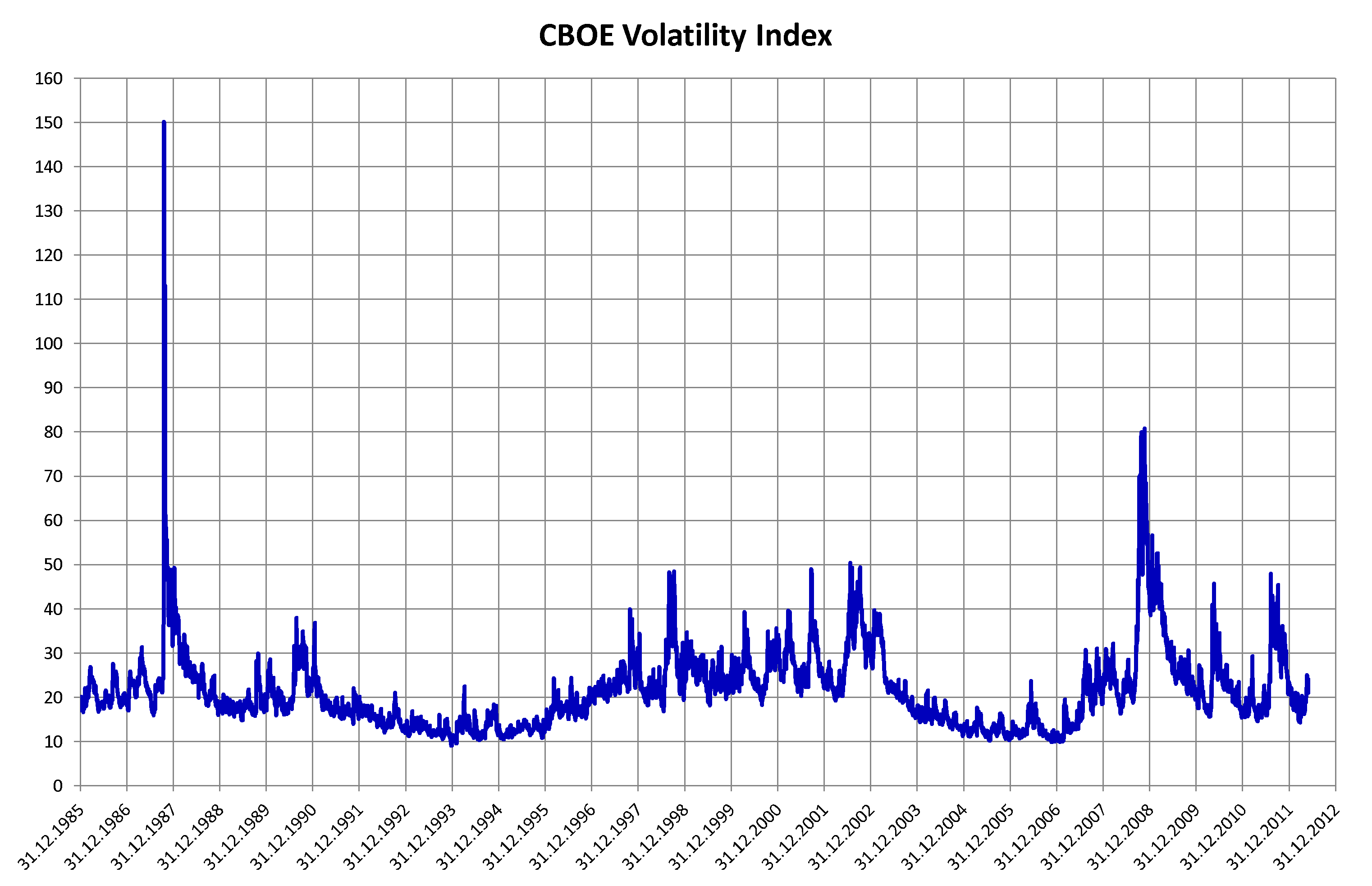
In finance, volatility (usually denoted by ''σ'') is the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn calculated using the sum of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Process
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, cryptography and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance. Applications and the study of phenomena have in turn inspired the proposal of new stochastic processes. Examples of such stochastic processes include the Wiener process or Brownian motion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noise Reduction
Noise reduction is the process of removing noise from a signal. Noise reduction techniques exist for audio and images. Noise reduction algorithms may distort the signal to some degree. Noise rejection is the ability of a circuit to isolate an undesired signal component from the desired signal component, as with common-mode rejection ratio. All signal processing devices, both analog and digital, have traits that make them susceptible to noise. Noise can be random with an even frequency distribution (white noise), or frequency-dependent noise introduced by a device's mechanism or signal processing algorithms. In electronic systems, a major type of noise is ''hiss'' created by random electron motion due to thermal agitation. These agitated electrons rapidly add and subtract from the output signal and thus create detectable noise. In the case of photographic film and magnetic tape, noise (both visible and audible) is introduced due to the grain structure of the medium. In photo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Foreign Exchange Market
The foreign exchange market (Forex, FX, or currency market) is a global decentralized or over-the-counter (OTC) market for the trading of currencies. This market determines foreign exchange rates for every currency. It includes all aspects of buying, selling and exchanging currencies at current or determined prices. In terms of trading volume, it is by far the largest market in the world, followed by the credit market. The main participants in this market are the larger international banks. Financial centers around the world function as anchors of trading between a wide range of multiple types of buyers and sellers around the clock, with the exception of weekends. Since currencies are always traded in pairs, the foreign exchange market does not set a currency's absolute value but rather determines its relative value by setting the market price of one currency if paid for with another. Ex: USD 1 is worth X CAD, or CHF, or JPY, etc. The foreign exchange market works ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Law
In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a proportional relative change in the other quantity, independent of the initial size of those quantities: one quantity varies as a power of another. For instance, considering the area of a square in terms of the length of its side, if the length is doubled, the area is multiplied by a factor of four. Empirical examples The distributions of a wide variety of physical, biological, and man-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words in most languages, frequencies of family names, the species richness in clades of organisms, the sizes of power outages, volcanic eruptions, human judgments of stimulus intensity and many other quantit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sharpe Ratio
In finance, the Sharpe ratio (also known as the Sharpe index, the Sharpe measure, and the reward-to-variability ratio) measures the performance of an investment such as a security or portfolio compared to a risk-free asset, after adjusting for its risk. It is defined as the difference between the returns of the investment and the risk-free return, divided by the standard deviation of the investment returns. It represents the additional amount of return that an investor receives per unit of increase in risk. It was named after William F. Sharpe, who developed it in 1966. Definition Since its revision by the original author, William Sharpe, in 1994, the ''ex-ante'' Sharpe ratio is defined as: : S_a = \frac = \frac, where R_a is the asset return, R_b is the risk-free return (such as a U.S. Treasury security). E_a-R_b/math> is the expected value of the excess of the asset return over the benchmark return, and is the standard deviation of the asset excess return. The ''ex-p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Market Liquidity
In business, economics or investment, market liquidity is a market's feature whereby an individual or firm can quickly purchase or sell an asset without causing a drastic change in the asset's price. Liquidity involves the trade-off between the price at which an asset can be sold, and how quickly it can be sold. In a liquid market, the trade-off is mild: one can sell quickly without having to accept a significantly lower price. In a relatively illiquid market, an asset must be discounted in order to sell quickly. Money, or cash, is the most liquid asset because it can be exchanged for goods and services instantly at face value. Overview A liquid asset has some or all of the following features: It can be sold rapidly, with minimal loss of value, anytime within market hours. The essential characteristic of a liquid market is that there are always ready and willing buyers and sellers. It is similar to, but distinct from, market depth, which relates to the trade-off between qua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Big Data
Though used sometimes loosely partly because of a lack of formal definition, the interpretation that seems to best describe Big data is the one associated with large body of information that we could not comprehend when used only in smaller amounts. In it primary definition though, Big data refers to data sets that are too large or complex to be dealt with by traditional data-processing application software. Data with many fields (rows) offer greater statistical power, while data with higher complexity (more attributes or columns) may lead to a higher false discovery rate. Big data analysis challenges include capturing data, data storage, data analysis, search, sharing, transfer, visualization, querying, updating, information privacy, and data source. Big data was originally associated with three key concepts: ''volume'', ''variety'', and ''velocity''. The analysis of big data presents challenges in sampling, and thus previously allowing for only observations and sampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CC-BY Icon
A Creative Commons (CC) license is one of several public copyright licenses that enable the free distribution of an otherwise copyrighted "work".A "work" is any creative material made by a person. A painting, a graphic, a book, a song/lyrics to a song, or a photograph of almost anything are all examples of "works". A CC license is used when an author wants to give other people the right to share, use, and build upon a work that the author has created. CC provides an author flexibility (for example, they might choose to allow only non-commercial uses of a given work) and protects the people who use or redistribute an author's work from concerns of copyright infringement as long as they abide by the conditions that are specified in the license by which the author distributes the work. There are several types of Creative Commons licenses. Each license differs by several combinations that condition the terms of distribution. They were initially released on December 16, 2002, by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |