|
De Sitter Precession
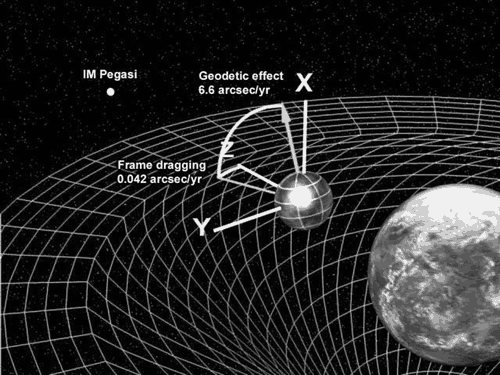
The geodetic effect (also known as geodetic precession, de Sitter precession or de Sitter effect) represents the effect of the curvature of spacetime, predicted by general relativity, on a vector carried along with an orbiting body. For example, the vector could be the angular momentum of a gyroscope orbiting the Earth, as carried out by the Gravity Probe B experiment. The geodetic effect was first predicted by Willem de Sitter in 1916, who provided relativistic corrections to the Earth–Moon system's motion. De Sitter's work was extended in 1918 by Jan Schouten and in 1920 by Adriaan Fokker. It can also be applied to a particular secular precession of astronomical orbits, equivalent to the rotation of the Laplace–Runge–Lenz vector. The term geodetic effect has two slightly different meanings as the moving body may be spinning or non-spinning. Non-spinning bodies move in geodesics, whereas spinning bodies move in slightly different orbits. The difference between de Sitter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravity Probe Turning Axis
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the strong interaction, 1036 times weaker than the electromagnetic force and 1029 times weaker than the weak interaction. As a result, it has no significant influence at the level of Subatomic particle, subatomic particles. However, gravity is the most significant interaction between objects at the macroscopic scale, and it determines the motion of Planet, planets, Star, stars, Galaxy, galaxies, and even Electromagnetic radiation, light. Gravity of Earth, On Earth, gravity gives weight to physical objects, and the gravitation of the Moon, Moon's gravity is responsible for sublunar tides in the oceans (the corresponding antipodal tide is caused by the inertia of the Earth and Moon orbiting one another). Gravity also has many important biological func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarzschild Metric
In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916, and around the same time independently by Johannes Droste, who published his more complete and modern-looking discussion four months after Schwarzschild. According to Birkhoff's theorem, the Schwarzschild metric is the most general spherically symmetric vacuum solution of the Einstein field equations. A Schwarzschild black hole or static black hole is a black hole that has neither electric charge nor angular momentum. A Schwar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Timeline Of Gravitational Physics And Relativity
The following is a timeline of gravitational physics and general relativity. Before 1500 * 3rd century BC - Aristarchus of Samos proposes heliocentric model, measures the distance to the Moon and its size 1500s * 1543 – Nicolaus Copernicus places the Sun at the gravitational center, starting a revolution in science * 1583 – Galileo Galilei induces the period relationship of a pendulum from observations (according to later biographer). * 1586 – Simon Stevin demonstrates that two objects of different mass accelerate at the same rate when dropped. * 1589 – Galileo Galilei describes a hydrostatic balance for measuring specific gravity. * 1590 – Galileo Galilei formulates modified Aristotelean theory of motion (later retracted) based on density rather than weight of objects. 1600s * 1602 – Galileo Galilei conducts experiments on pendulum motion. * 1604 – Galileo Galilei conducts experiments with inclined planes and induces the law of falling objects. * 1607 – Galileo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravity Well
The Hill sphere of an astronomical body is the region in which it dominates the attraction of satellites. To be retained by a planet, a moon must have an orbit that lies within the planet's Hill sphere. That moon would, in turn, have a Hill sphere of its own. Any object within that distance would tend to become a satellite of the moon, rather than of the planet itself. One simple view of the extent of the Solar System is the Hill sphere of the Sun with respect to local stars and the galactic nucleus. In more precise terms, the Hill sphere approximates the gravitational sphere of influence of a smaller body in the face of perturbations from a more massive body. It was defined by the American astronomer George William Hill, based on the work of the French astronomer Édouard Roche. In the example to the right, the Earth's Hill sphere extends between the Lagrange points and , which lie along the line of centers of the two bodies. The region of influence of the smaller body is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesics In General Relativity
In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational forces is a particular type of geodesic. In other words, a freely moving or falling particle always moves along a geodesic. In general relativity, gravity can be regarded as not a force but a consequence of a general relativity, curved spacetime geometry where the source of curvature is the stress–energy tensor (representing matter, for instance). Thus, for example, the path of a planet orbiting a star is the projection of a geodesic of the curved four-dimensional (4-D) spacetime geometry around the star onto three-dimensional (3-D) space. Mathematical expression The full geodesic equation is : +\Gamma^\mu _=0\ where ''s'' is a scalar parameter of motion (e.g. the proper time), and \Gamma^\mu _ are Christoffel symbols (sometimes called the affine connection coefficients or Levi-Civita connectio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frame-dragging
Frame-dragging is an effect on spacetime, predicted by Albert Einstein's general theory of relativity, that is due to non-static stationary distributions of mass–energy. A stationary field is one that is in a steady state, but the masses causing that field may be non-static — rotating, for instance. More generally, the subject that deals with the effects caused by mass–energy currents is known as gravitoelectromagnetism, which is analogous to the magnetism of classical electromagnetism. The first frame-dragging effect was derived in 1918, in the framework of general relativity, by the Austrian physicists Josef Lense and Hans Thirring, and is also known as the Lense–Thirring effect. They predicted that the rotation of a massive object would distort the spacetime metric, making the orbit of a nearby test particle precess. This does not happen in Newtonian mechanics for which the gravitational field of a body depends only on its mass, not on its rotation. The Lense ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas Precession
In physics, the Thomas precession, named after Llewellyn Thomas, is a relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope and relates the angular velocity of the spin of a particle following a curvilinear orbit to the angular velocity of the orbital motion. For a given inertial frame, if a second frame is Lorentz-boosted relative to it, and a third boosted relative to the second, but non-colinear with the first boost, then the Lorentz transformation between the first and third frames involves a combined boost and rotation, known as the "Wigner rotation" or "Thomas rotation". For accelerated motion, the accelerated frame has an inertial frame at every instant. Two boosts a small time interval (as measured in the lab frame) apart leads to a Wigner rotation after the second boost. In the limit the time interval tends to zero, the accelerated frame will rotate at every instant, so the accelerated frame rotates w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinematic
Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics. Kinematics is used in astrophysics to describe the motion of celestial bodies and collections of such bodies. In mechanical engineering, robotics, and biomechanics kinematics is us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series, when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. It is thus independent of coordinates, and is a Lorentz scalar. The proper time interval between two events on a world line is the change in proper time. This interval is the quantity of interest, since proper time itself is fixed only up to an arbitrary additive constant, namely the setting of the clock at some event along the world line. The proper time interval between two events depends not only on the events, but also the world line connecting them, and hence on the motion of the clock between the events. It is expressed as an integral over the world line (analogous to arc length in Euclidean space). An accelerated clock will measure a smaller elapsed time between two events than that measured by a non-accelerated (inertial) clock between the same two events. The twin paradox is an example of this effect. By convention, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler's Laws
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that: # The orbit of a planet is an ellipse with the Sun at one of the two foci. # A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. # The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law helps to establish that when a planet is closer to the Sun, it travels faster. The third law ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.gif)
