|
Cosmological Constant
In cosmology, the cosmological constant (usually denoted by the Greek capital letter lambda: ), alternatively called Einstein's cosmological constant, is the constant coefficient of a term that Albert Einstein temporarily added to his field equations of general relativity. He later removed it. Much later it was revived and reinterpreted as the energy density of space, or vacuum energy, that arises in quantum mechanics. It is closely associated with the concept of dark energy. Einstein originally introduced the constant in 1917 to counterbalance the effect of gravity and achieve a static universe, a notion that was the accepted view at the time. Einstein's cosmological constant was abandoned after Edwin Hubble's confirmation that the universe was expanding. From the 1930s until the late 1990s, most physicists agreed with Einstein's choice of setting the cosmological constant to zero. That changed with the discovery in 1998 that the expansion of the universe is accelerating ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CMB Timeline300 No WMAP
In Big Bang cosmology the cosmic microwave background (CMB, CMBR) is electromagnetic radiation that is a remnant from an early stage of the universe, also known as "relic radiation". The CMB is faint cosmic background radiation filling all space. It is an important source of data on the early universe because it is the oldest electromagnetic radiation in the universe, dating to the epoch of recombination when the first atoms were formed. With a traditional optical telescope, the space between stars and galaxies (the background) is completely dark (see: Olbers' paradox). However, a sufficiently sensitive radio telescope shows a faint background brightness, or glow, almost isotropic, uniform, that is not associated with any star, galaxy, or other astronomical object, object. This glow is strongest in the microwave region of the radio spectrum. The accidental Discovery of cosmic microwave background radiation, discovery of the CMB in 1965 by American radio astronomers Arno Penzias an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Fields
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. QFT treats particles as excited states (also called quanta) of their underlying quantum fields, which are more fundamental than the particles. The equation of motion of the particle is determined by minimization of the Lagrangian, a functional of fields associated with the particle. Interactions between particles are described by interaction terms in the Lagrangian involving their corresponding quantum fields. Each interaction can be visually represented by Feynman diagrams according to perturbation theory in quantum mechanics. History Quantum field theory emerged from the work of generations of theoretical physicists spanning much of the 20th century. Its developm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Connection
In differential geometry, an affine connection is a geometric object on a smooth manifold which ''connects'' nearby tangent spaces, so it permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space. Connections are among the simplest methods of defining differentiation of the sections of vector bundles. The notion of an affine connection has its roots in 19th-century geometry and tensor calculus, but was not fully developed until the early 1920s, by Élie Cartan (as part of his general theory of connections) and Hermann Weyl (who used the notion as a part of his foundations for general relativity). The terminology is due to Cartan and has its origins in the identification of tangent spaces in Euclidean space by translation: the idea is that a choice of affine connection makes a manifold look infinitesimally like Euclidean space not just smoothly, but as an affine space. On any manifold of positive dimension ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger (, ; ; 12 August 1887 – 4 January 1961), sometimes written as or , was a Nobel Prize-winning Austrian physicist with Irish citizenship who developed a number of fundamental results in quantum theory: the Schrödinger equation provides a way to calculate the wave function of a system and how it changes dynamically in time. In addition, he wrote many works on various aspects of physics: statistical mechanics and thermodynamics, physics of dielectrics, colour theory, electrodynamics, general relativity, and cosmology, and he made several attempts to construct a unified field theory. In his book '' What Is Life?'' Schrödinger addressed the problems of genetics, looking at the phenomenon of life from the point of view of physics. He also paid great attention to the philosophical aspects of science, ancient, and oriental philosophical concepts, ethics, and religion. He also wrote on philosophy and theoretical biology. In popular cult ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauge Theory
In physics, a gauge theory is a type of field theory in which the Lagrangian (and hence the dynamics of the system itself) does not change (is invariant) under local transformations according to certain smooth families of operations (Lie groups). The term ''gauge'' refers to any specific mathematical formalism to regulate redundant degrees of freedom in the Lagrangian of a physical system. The transformations between possible gauges, called ''gauge transformations'', form a Lie group—referred to as the ''symmetry group'' or the ''gauge group'' of the theory. Associated with any Lie group is the Lie algebra of group generators. For each group generator there necessarily arises a corresponding field (usually a vector field) called the ''gauge field''. Gauge fields are included in the Lagrangian to ensure its invariance under the local group transformations (called ''gauge invariance''). When such a theory is quantized, the quanta of the gauge fields are called '' gauge boson ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epistemology
Epistemology (; ), or the theory of knowledge, is the branch of philosophy concerned with knowledge. Epistemology is considered a major subfield of philosophy, along with other major subfields such as ethics, logic, and metaphysics. Epistemologists study the nature, origin, and scope of knowledge, epistemic justification, the rationality of belief, and various related issues. Debates in epistemology are generally clustered around four core areas: # The philosophical analysis of the nature of knowledge and the conditions required for a belief to constitute knowledge, such as truth and justification # Potential sources of knowledge and justified belief, such as perception, reason, memory, and testimony # The structure of a body of knowledge or justified belief, including whether all justified beliefs must be derived from justified foundational beliefs or whether justification requires only a coherent set of beliefs # Philosophical skepticism, which questions the pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arthur Stanley Eddington
Sir Arthur Stanley Eddington (28 December 1882 – 22 November 1944) was an English astronomer, physicist, and mathematician. He was also a philosopher of science and a populariser of science. The Eddington limit, the natural limit to the luminosity of stars, or the radiation generated by accretion onto a compact object, is named in his honour. Around 1920, he foreshadowed the discovery and mechanism of nuclear fusion processes in stars, in his paper "The Internal Constitution of the Stars".The Internal Constitution of the Stars A. S. Eddington The Scientific Monthly Vol. 11, No. 4 (Oct., 1920), pp. 297–303 At that time, the source of stellar energy was a complete mystery; Eddington was the first to correctly speculate that the source was fusion of hydrogen into helium. Eddington wrote a number of articles that announced and explained Einstein's theory of general relativity to the English-speaking world. World War I had severed many lines of scientific communication, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Unified Field Theories
Since the 19th century, some physicists, notably Albert Einstein, have attempted to develop a single theoretical framework that can account for all the fundamental forces of nature – a unified field theory. Classical unified field theories are attempts to create a unified field theory based on classical physics. In particular, unification of gravitation and electromagnetism was actively pursued by several physicists and mathematicians in the years between the two World Wars. This work spurred the purely mathematical development of differential geometry. This article describes various attempts at formulating a classical (non- quantum), relativistic unified field theory. For a survey of classical relativistic field theories of gravitation that have been motivated by theoretical concerns other than unification, see Classical theories of gravitation. For a survey of current work toward creating a quantum theory of gravitation, see quantum gravity. Overview The early attempts a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
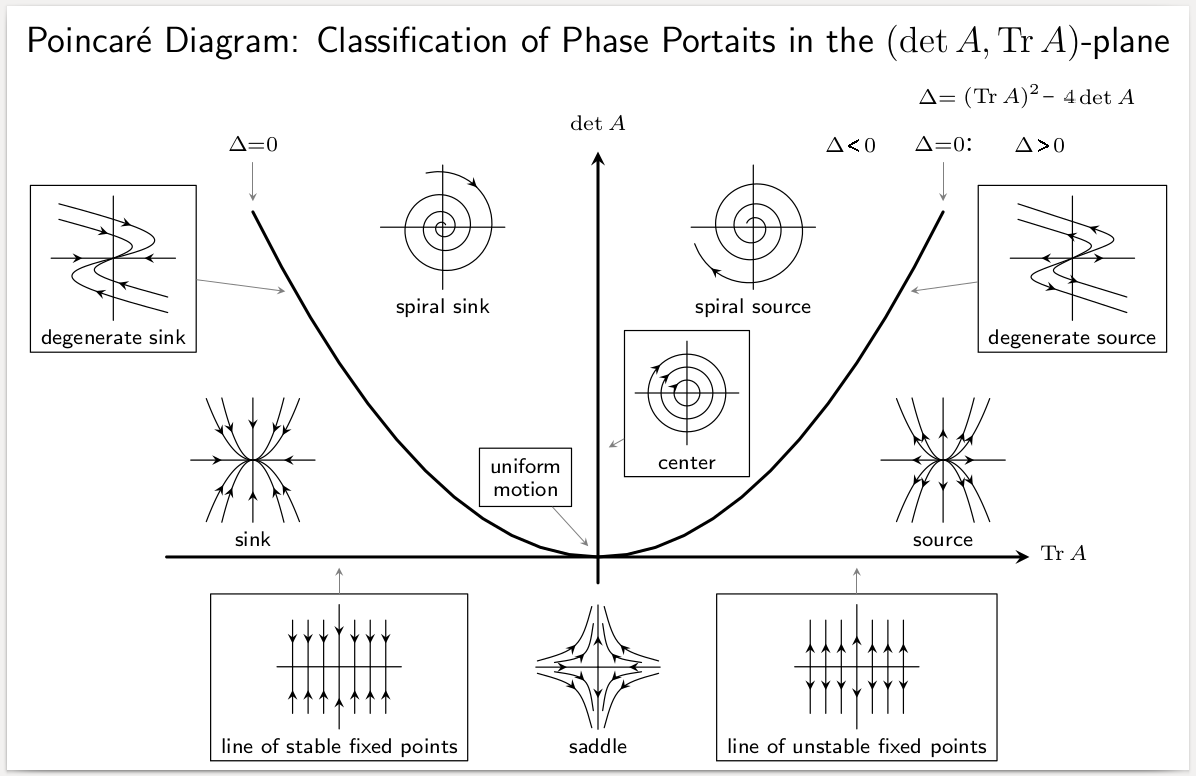
Equilibrium Point
In mathematics, specifically in differential equations, an equilibrium point is a constant solution to a differential equation. Formal definition The point \tilde\in \mathbb^n is an equilibrium point for the differential equation :\frac = \mathbf(t,\mathbf) if \mathbf(t,\tilde)=\mathbf for all t. Similarly, the point \tilde\in \mathbb^n is an equilibrium point (or fixed point) for the difference equation :\mathbf_ = \mathbf(k,\mathbf_k) if \mathbf(k,\tilde)= \tilde for k=0,1,2,\ldots. Equilibria can be classified by looking at the signs of the eigenvalues of the linearization of the equations about the equilibria. That is to say, by evaluating the Jacobian matrix at each of the equilibrium points of the system, and then finding the resulting eigenvalues, the equilibria can be categorized. Then the behavior of the system in the neighborhood of each equilibrium point can be qualitatively determined, (or even quantitatively determined, in some instances), by finding t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Redshift
In physics, a redshift is an increase in the wavelength, and corresponding decrease in the frequency and photon energy, of electromagnetic radiation (such as light). The opposite change, a decrease in wavelength and simultaneous increase in frequency and energy, is known as a negative redshift, or blueshift. The terms derive from the colours red and blue which form the extremes of the visible light spectrum. In astronomy and cosmology, the three main causes of electromagnetic redshift are # The radiation travels between objects which are moving apart (" relativistic" redshift, an example of the relativistic Doppler effect) #The radiation travels towards an object in a weaker gravitational potential, i.e. towards an object in less strongly curved (flatter) spacetime ( gravitational redshift) #The radiation travels through expanding space ( cosmological redshift). The observation that all sufficiently distant light sources show redshift corresponding to their distance fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexander Alexandrovich Friedmann
Alexander Alexandrovich Friedmann (also spelled Friedman or Fridman ; russian: Алекса́ндр Алекса́ндрович Фри́дман) (June 16 .S. 4 1888 – September 16, 1925) was a Russian and Soviet physicist and mathematician. He is best known for his pioneering theory that the universe was expanding, governed by a set of equations he developed now known as the Friedmann equations. Early life Alexander Friedmann was born to the composer and ballet dancer Alexander Friedmann (who was a son of a baptized Jewish cantonist) and the pianist Ludmila Ignatievna Voyachek (who was a daughter of the Czech composer Hynek Vojáček). Friedmann was baptized into the Russian Orthodox Church as an infant, and lived much of his life in Saint Petersburg. Friedmann obtained his degree from St. Petersburg State University in 1910, and became a lecturer at Saint Petersburg Mining Institute. From his school days, Friedmann found a lifelong companion in Jacob Tamarkin, who was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein Field Equations
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it. The equations were published by Einstein in 1915 in the form of a tensor equation which related the local ' (expressed by the Einstein tensor) with the local energy, momentum and stress within that spacetime (expressed by the stress–energy tensor). Analogously to the way that electromagnetic fields are related to the distribution of charges and currents via Maxwell's equations, the EFE relate the spacetime geometry to the distribution of mass–energy, momentum and stress, that is, they determine the metric tensor of spacetime for a given arrangement of stress–energy–momentum in the spacetime. The relationship between the metric tensor and the Einstein tensor allows the EFE to be written as a set of nonlinear partial differential equations when used in this way. The solutions of the EF ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |