|
Comeager Set
In the Mathematics, mathematical field of general topology, a meagre set (also called a meager set or a set of first category) is a subset of a topological space that is small or Negligible set, negligible in a precise sense detailed below. A set that is not meagre is called nonmeagre, or of the second category. See below for definitions of other related terms. The meagre subsets of a fixed space form a Sigma-ideal, σ-ideal of subsets; that is, any subset of a meagre set is meagre, and the union (set theory), union of Countable set, countably many meagre sets is meagre. Meagre sets play an important role in the formulation of the notion of Baire space and of the Baire category theorem, which is used in the proof of several fundamental results of functional analysis. Definitions Throughout, X will be a topological space. A subset of X is called X, a of X, or of the in X if it is a countable union of nowhere dense subsets of X (where a nowhere dense set is a set whose closur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
René Baire
René (''born again'' or ''reborn'' in French) is a common first name in French-speaking, Spanish-speaking, and German-speaking countries. It derives from the Latin name Renatus. René is the masculine form of the name (Renée being the feminine form). In some non-Francophone countries, however, there exists the habit of giving the name René (sometimes spelled without an accent) to girls as well as boys. In addition, both forms are used as surnames (family names). René as a first name given to boys in the United States reached its peaks in popularity in 1969 and 1983 when it ranked 256th. Since 1983 its popularity has steadily declined and it ranked 881st in 2016. René as a first name given to girls in the United States reached its peak in popularity in 1962 when it ranked 306th. The last year for which René was ranked in the top 1000 names given to girls in the United States was 1988. Persons with the given name * René, Duke of Anjou (1409–1480), titular king of Naples ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
T1 Space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has a neighborhood not containing the other point. An R0 space is one in which this holds for every pair of topologically distinguishable points. The properties T1 and R0 are examples of separation axioms. Definitions Let ''X'' be a topological space In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called points ... and let ''x'' and ''y'' be points in ''X''. We say that ''x'' and ''y'' are if each lies in a neighbourhood (mathematics), neighbourhood that does not contain the other point. * ''X'' is called a T1 space if any two distinct points in ''X'' are separated. * ''X'' is called an R0 space if any two topologically distinguishable points in ''X'' are separa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Open Set
In mathematics, open sets are a generalization of open intervals in the real line. In a metric space (a set along with a distance defined between any two points), open sets are the sets that, with every point , contain all points that are sufficiently near to (that is, all points whose distance to is less than some value depending on ). More generally, one defines open sets as the members of a given collection of subsets of a given set, a collection that has the property of containing every union of its members, every finite intersection of its members, the empty set, and the whole set itself. A set in which such a collection is given is called a topological space, and the collection is called a topology. These conditions are very loose, and allow enormous flexibility in the choice of open sets. For example, ''every'' subset can be open (the discrete topology), or no set can be open except the space itself and the empty set (the indiscrete topology). In practice, however, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gδ Set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in German with ''G'' for '' Gebiet'' (''German'': area, or neighbourhood) meaning open set in this case and for '' Durchschnitt'' (''German'': intersection).. Historically Gδ sets were also called inner limiting sets, but that terminology is not in use anymore. Gδ sets, and their dual, F sets, are the second level of the Borel hierarchy. Definition In a topological space a Gδ set is a countable intersection of open sets. The Gδ sets are exactly the level Π sets of the Borel hierarchy. Examples * Any open set is trivially a Gδ set. * The irrational numbers are a Gδ set in the real numbers \R. They can be written as the countable intersection of the open sets \^ (the superscript denoting the complement) where q is rational. * The set of rational numbers \Q is a Gδ set in \R. If \Q were the intersection of open set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interior (topology)
In mathematics, specifically in general topology, topology, the interior of a subset of a topological space is the Union (set theory), union of all subsets of that are Open set, open in . A point that is in the interior of is an interior point of . The interior of is the Absolute complement, complement of the closure (topology), closure of the complement of . In this sense interior and closure are Duality_(mathematics)#Duality_in_logic_and_set_theory, dual notions. The exterior of a set is the complement of the closure of ; it consists of the points that are in neither the set nor its boundary (topology), boundary. The interior, boundary, and exterior of a subset together partition of a set, partition the whole space into three blocks (or fewer when one or more of these is empty set, empty). Definitions Interior point If is a subset of a Euclidean space, then is an interior point of if there exists an open ball centered at which is completely contained in . (This is i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fσ Set
In mathematics, an Fσ set (said F-sigma set) is a countable union of closed sets. The notation originated in French with F for (''French'': closed) and σ for (''French'': sum, union).. The complement of an Fσ set is a Gδ set. Fσ is the same as \mathbf^0_2 in the Borel hierarchy. Examples Each closed set is an Fσ set. The set \mathbb of rationals is an Fσ set in \mathbb. More generally, any countable set in a T1 space is an Fσ set, because every singleton \ is closed. The set \mathbb\setminus\mathbb of irrationals is not a Fσ set. In metrizable spaces, every open set is an Fσ set.. The union of countably many Fσ sets is an Fσ set, and the intersection of finitely many Fσ sets is an Fσ set. The set A of all points (x,y) in the Cartesian plane such that x/y is rational is an Fσ set because it can be expressed as the union of all the lines passing through the origin with rational slope: : A = \bigcup_ \, where \mathbb, is the set of rational number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
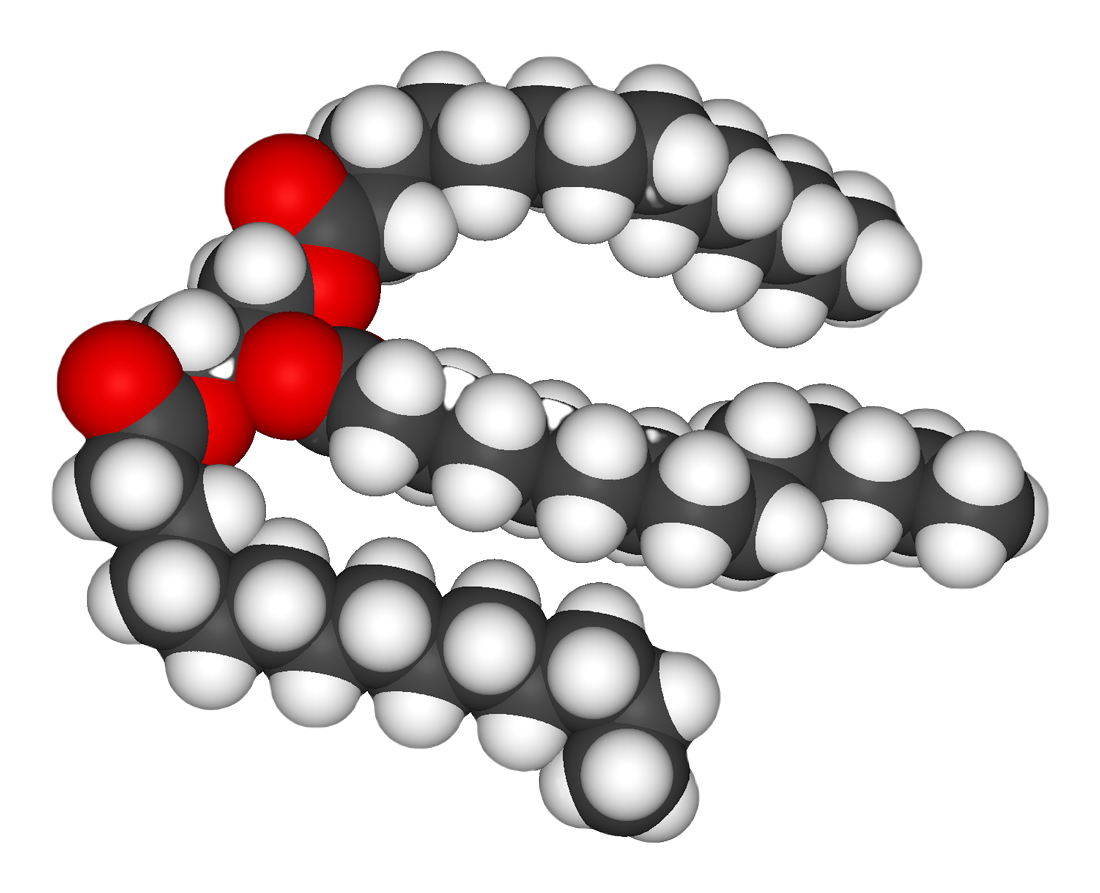
Fat Cantor Set
In nutrition, biology, and chemistry, fat usually means any ester of fatty acids, or a mixture of such compounds, most commonly those that occur in living beings or in food. The term often refers specifically to triglycerides (triple esters of glycerol), that are the main components of vegetable oils and of fatty tissue in animals; or, even more narrowly, to triglycerides that are solid or semisolid at room temperature, thus excluding oils. The term may also be used more broadly as a synonym of lipid—any substance of biological relevance, composed of carbon, hydrogen, or oxygen, that is insoluble in water but soluble in non-polar solvents. In this sense, besides the triglycerides, the term would include several other types of compounds like mono- and diglycerides, phospholipids (such as lecithin), sterols (such as cholesterol), waxes (such as beeswax), and free fatty acids, which are usually present in human diet in smaller amounts. Fats are one of the three main mac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lebesgue Measure
In measure theory, a branch of mathematics, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of ''n''-dimensional Euclidean space. For ''n'' = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called ''n''-dimensional volume, ''n''-volume, or simply volume. It is used throughout real analysis, in particular to define Lebesgue integration. Sets that can be assigned a Lebesgue measure are called Lebesgue-measurable; the measure of the Lebesgue-measurable set ''A'' is here denoted by ''λ''(''A''). Henri Lebesgue described this measure in the year 1901, followed the next year by his description of the Lebesgue integral. Both were published as part of his dissertation in 1902. Definition For any interval I = ,b/math>, or I = (a, b), in the set \mathbb of real numbers, let \ell(I)= b - a denote its length. For any subset E\subseteq\mathbb, the Lebesgue oute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Compact Hausdorff
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space. More precisely, it is a topological space in which every point has a compact neighborhood. In mathematical analysis locally compact spaces that are Hausdorff are of particular interest; they are abbreviated as LCH spaces. Formal definition Let ''X'' be a topological space. Most commonly ''X'' is called locally compact if every point ''x'' of ''X'' has a compact neighbourhood, i.e., there exists an open set ''U'' and a compact set ''K'', such that x\in U\subseteq K. There are other common definitions: They are all equivalent if ''X'' is a Hausdorff space (or preregular). But they are not equivalent in general: :1. every point of ''X'' has a compact neighbourhood. :2. every point of ''X'' has a closed compact neighbourhood. :2′. every point of ''X'' has a relatively compact neighbourhood ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Metric Space
In mathematical analysis, a metric space is called complete (or a Cauchy space) if every Cauchy sequence of points in has a limit that is also in . Intuitively, a space is complete if there are no "points missing" from it (inside or at the boundary). For instance, the set of rational numbers is not complete, because e.g. \sqrt is "missing" from it, even though one can construct a Cauchy sequence of rational numbers that converges to it (see further examples below). It is always possible to "fill all the holes", leading to the ''completion'' of a given space, as explained below. Definition Cauchy sequence A sequence x_1, x_2, x_3, \ldots in a metric space (X, d) is called Cauchy if for every positive real number r > 0 there is a positive integer N such that for all positive integers m, n > N, d\left(x_m, x_n\right) < r. Complete space A metric space is complete if any of the following equivalent conditions are satisfied: :#Every |
Discrete Space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points form a , meaning they are '' isolated'' from each other in a certain sense. The discrete topology is the finest topology that can be given on a set. Every subset is open in the discrete topology so that in particular, every singleton subset is an open set in the discrete topology. Definitions Given a set X: A metric space (E,d) is said to be '' uniformly discrete'' if there exists a ' r > 0 such that, for any x,y \in E, one has either x = y or d(x,y) > r. The topology underlying a metric space can be discrete, without the metric being uniformly discrete: for example the usual metric on the set \left\. Properties The underlying uniformity on a discrete metric space is the discrete uniformity, and the underlying topology on a discrete uniform space is the discrete topology. Thus, the different notions of discrete space are compatible with one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |