|
Combinatorial
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science. Combinatorics is well known for the breadth of the problems it tackles. Combinatorial problems arise in many areas of pure mathematics, notably in algebra, probability theory, topology, and geometry, as well as in its many application areas. Many combinatorial questions have historically been considered in isolation, giving an ''ad hoc'' solution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right. One of the oldest and most accessible parts of combinatorics is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Discrete Mathematics
Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection with the set of natural numbers) rather than "continuous" (analogously to continuous functions). Objects studied in discrete mathematics include integers, Graph (discrete mathematics), graphs, and Statement (logic), statements in Mathematical logic, logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumeration, enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets (finite sets or sets with the same cardinality as the natural numbers). However, there is no exact definition of the term "discrete mathematics". The set of objects studied in discrete mathematics can be finite or infinite. The term finite mathematics is sometime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Counting
Counting is the process of determining the number of elements of a finite set of objects; that is, determining the size of a set. The traditional way of counting consists of continually increasing a (mental or spoken) counter by a unit for every element of the set, in some order, while marking (or displacing) those elements to avoid visiting the same element more than once, until no unmarked elements are left; if the counter was set to one after the first object, the value after visiting the final object gives the desired number of elements. The related term ''enumeration'' refers to uniquely identifying the elements of a finite (combinatorial) set or infinite set by assigning a number to each element. Counting sometimes involves numbers other than one; for example, when counting money, counting out change, "counting by twos" (2, 4, 6, 8, 10, 12, ...), or "counting by fives" (5, 10, 15, 20, 25, ...). There is archaeological evidence suggesting that humans have been ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Analysis Of Algorithms
In computer science, the analysis of algorithms is the process of finding the computational complexity of algorithms—the amount of time, storage, or other resources needed to execute them. Usually, this involves determining a function that relates the size of an algorithm's input to the number of steps it takes (its time complexity) or the number of storage locations it uses (its space complexity). An algorithm is said to be efficient when this function's values are small, or grow slowly compared to a growth in the size of the input. Different inputs of the same size may cause the algorithm to have different behavior, so best, worst and average case descriptions might all be of practical interest. When not otherwise specified, the function describing the performance of an algorithm is usually an upper bound, determined from the worst case inputs to the algorithm. The term "analysis of algorithms" was coined by Donald Knuth. Algorithm analysis is an important part of a broa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sushruta
Suśruta (, ) is the listed author of the '' Suśruta Saṃhiāa'' (''Suśruta's Compendium''), considered to be one of the most important surviving ancient treatises on medicine. It is also considered a foundational text of Ayurveda. The treatise addresses all aspects of general medicine, including diet, surgery, nosology, anatomy, developmental biology, therapeutics, toxicology, pediatrics and other subjects. The inclusion of particularly impressive and historically important chapters on surgery has wrongly led some to believe that this is the work's primary focus. The treatise consists of 186 chapters. The ''Compendium of Suśruta'' locates its author in Varanasi, India. Authorship The printed editions of the work normally contain the phrase "as Lord Dhanvantari declared" (Sanskrit ''यथोवाच भगवान्धन्वन्तरिः'') at the start of each chapter, framing the work as Dhanvantari's discourse. However, the earliest manuscripts of the wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Physician
A physician, medical practitioner (British English), medical doctor, or simply doctor is a health professional who practices medicine, which is concerned with promoting, maintaining or restoring health through the Medical education, study, Medical diagnosis, diagnosis, prognosis and therapy, treatment of disease, injury, and other physical and mental impairments. Physicians may focus their practice on certain disease categories, types of patients, and methods of treatment—known as Specialty (medicine), specialities—or they may assume responsibility for the provision of continuing and comprehensive medical care to individuals, families, and communities—known as general practitioner, general practice. Medical practice properly requires both a detailed knowledge of the Discipline (academia), academic disciplines, such as anatomy and physiology, pathophysiology, underlying diseases, and their treatment, which is the science of medicine, and a decent Competence (human resources ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
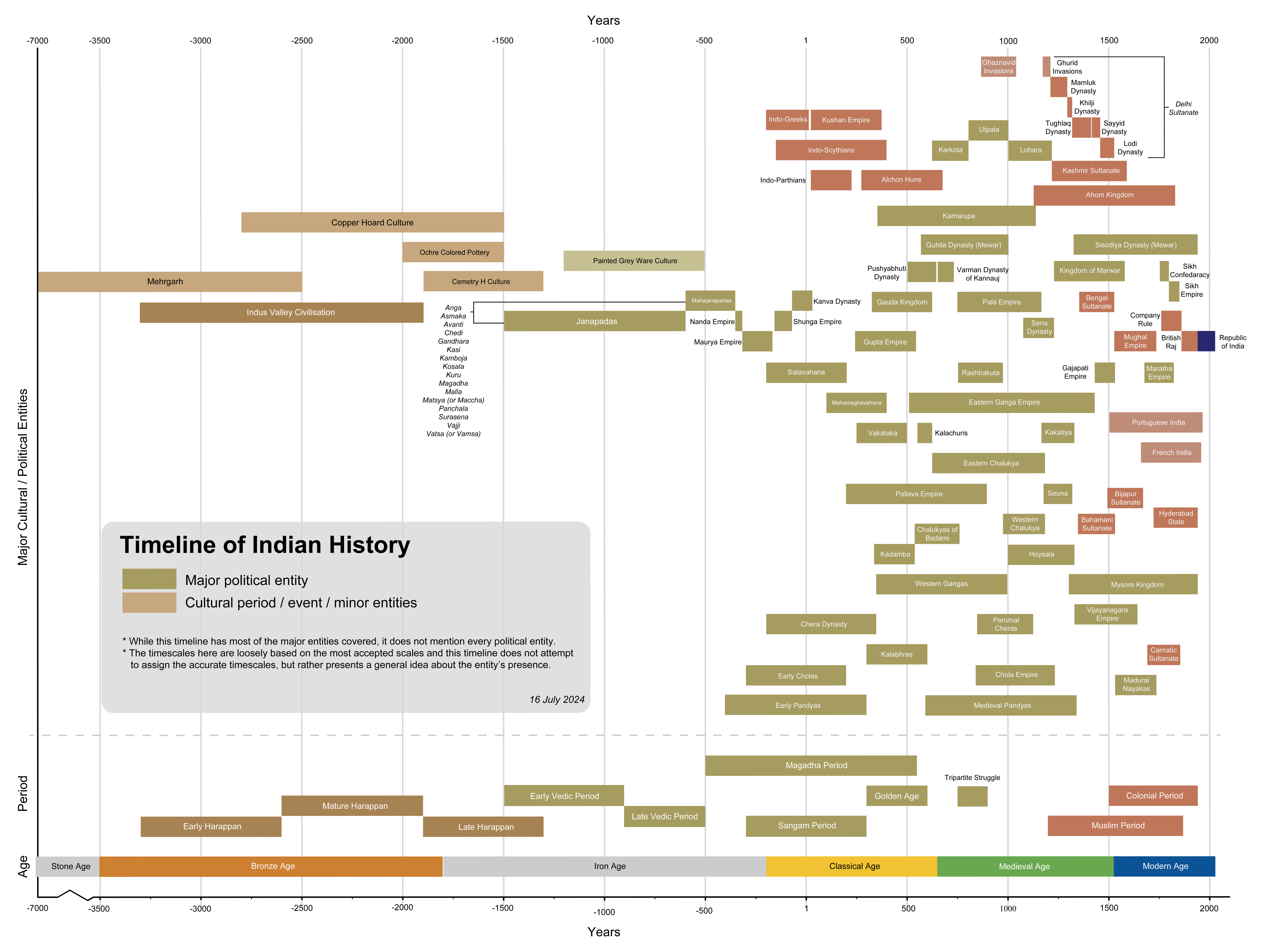
Timeline Of Indian History
This is a timeline of Indian history, comprising important legal and territorial changes and political events in India and its predecessor states. To read about the background to these events, see History of India. Also see the list of governors-general of India, list of prime ministers of India and list of years in India. Pre-historic India Pre-90th century BCE (BC) 90th–50th century BCE Bronze Age India 50th–40th century BCE 30th– 20th century BCE 19th century BCE 18th century BCE Iron Age India 17th century BCE 16th century BCE 15th century BCE 14th century BCE 13th century BCE 12th century BCE 11th century BCE 10th century BCE 9th century BCE 8th century BCE 7th century BCE 6th century BCE 5th century BCE 4th century BCE Classical India 3rd century BCE 2nd century BCE 1st century BCE 1st century 2nd century 3rd century ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ancient History
Ancient history is a time period from the History of writing, beginning of writing and recorded human history through late antiquity. The span of recorded history is roughly 5,000 years, beginning with the development of Sumerian language, Sumerian cuneiform script. Ancient history covers all continents inhabited by humans in the period 3000 BCAD 500, ending with the Early Muslim conquests, expansion of Islam in late antiquity. The three-age system periodises ancient history into the Stone Age, the Bronze Age, and the Iron Age, with recorded history generally considered to begin with the Bronze Age. The start and end of the three ages vary between world regions. In many regions the Bronze Age is generally considered to begin a few centuries prior to 3000 BC, while the end of the Iron Age varies from the early first millennium BC in some regions to the late first millennium AD in others. During the time period of ancient history, the world population was Exponential growth, e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sushruta Samhita
The ''Sushruta Samhita'' (, ) is an ancient Sanskrit text on medicine and one of the most important such treatises on this subject to survive from the ancient world. The ''Compendium of Sushruta, Suśruta'' is one of the foundational texts of Ayurveda (Indian traditional medicine originating from the Atharvaveda), alongside the ''Charaka Samhita, Charaka-Saṃhitā'', ''the Bhela Samhita, Bhela-Saṃhitā'', and the medical portions of the Bower Manuscript. It is one of the two foundational Hindu texts on the medical profession that have survived from ancient India. The ''Suśrutasaṃhitā'' is of great historical importance because it includes historically unique chapters describing surgical training, instruments and procedures. The oldest surviving manuscript of the ''Suśrutasaṃhitā'' is MS Kathmandu KL 699, a palm-leaf manuscript preserved at the Kaiser library, Kaiser Library, Nepal that is datable to 878 CE. History Date The most detailed and extensive considerati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Composition (combinatorics)
In mathematics, a composition of an integer ''n'' is a way of writing ''n'' as the summation, sum of a sequence of (strictly) positive integers. Two sequences that differ in the order of their terms define different compositions of their sum, while they are considered to define the same integer partition of that number. Every integer has finitely many distinct compositions. Negative numbers do not have any compositions, but 0 has one composition, the empty sequence. Each positive integer ''n'' has 2''n''−1 distinct compositions. A weak composition of an integer ''n'' is similar to a composition of ''n'', but allowing terms of the sequence to be zero: it is a way of writing ''n'' as the sum of a sequence of non-negative integers. As a consequence every positive integer admits infinitely many weak compositions (if their length is not bounded). Adding a number of terms 0 to the ''end'' of a weak composition is usually not considered to define a different weak composition; in other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |