Colored Matroid
In mathematics, a colored matroid is a matroid whose elements are labeled from a set of colors, which can be any set that suits the purpose, for instance the set of the first ''n'' positive integers, or the sign set . The interest in colored matroids is through their invariants, especially the colored Tutte polynomial, which generalizes the Tutte polynomial of a signed graph of . There has also been study of optimization problems on matroids where the objective function of the optimization depends on the set of colors chosen as part of a matroid basis.. See also * Bipartite matroid *Rota's basis conjecture In linear algebra and matroid, matroid theory, Rota's basis conjecture is an unproven conjecture concerning rearrangements of Basis (linear algebra), bases, named after Gian-Carlo Rota. It states that, if ''X'' is either a vector space of dimension ... References Matroid theory {{Combin-stub ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Matroid
In combinatorics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid Axiomatic system, axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or ''flats''. In the language of partially ordered sets, a finite simple matroid is equivalent to a geometric lattice. Matroid theory borrows extensively from the terms used in both linear algebra and graph theory, largely because it is the abstraction of various notions of central importance in these fields. Matroids have found applications in geometry, topology, combinatorial optimization, network theory, and coding theory. Definition There are many Cryptomorphism, equivalent ways to define a (finite) matroid. Independent sets In terms of independence, a finite matroid M is a pair (E, \mathcal), where E is a finite set (called the ''gro ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Tutte Polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a graph polynomial. It is a polynomial in two variables which plays an important role in graph theory. It is defined for every undirected graph G and contains information about how the graph is connected. It is denoted by T_G. The importance of this polynomial stems from the information it contains about G. Though originally studied in algebraic graph theory as a generalization of counting problems related to graph coloring and nowhere-zero flow, it contains several famous other specializations from other sciences such as the Jones polynomial from knot theory and the partition functions of the Potts model from statistical physics. It is also the source of several central computational problems in theoretical computer science. The Tutte polynomial has several equivalent definitions. It is essentially equivalent to Whitney’s rank polynomial, Tutte’s own dichromatic polynomial and Fortuin ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

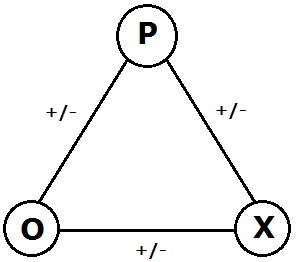
Signed Graph
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign. A signed graph is balanced if the product of edge signs around every cycle is positive. The name "signed graph" and the notion of balance appeared first in a mathematical paper of Frank Harary in 1953. Dénes Kőnig had already studied equivalent notions in 1936 under a different terminology but without recognizing the relevance of the sign group. At the Center for Group Dynamics at the University of Michigan, Dorwin Cartwright and Harary generalized Fritz Heider's psychological theory of balance in triangles of sentiments to a psychological theory of balance in signed graphs. Signed graphs have been rediscovered many times because they come up naturally in many unrelated areas. For instance, they enable one to describe and analyze the geometry of subsets of the classical root systems. They appear in topological graph theory and group theory. They are ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Bipartite Matroid
Bipartite may refer to: * 2 (number) * Bipartite (theology), a philosophical term describing the human duality of body and soul * Bipartite graph, in mathematics, a graph in which the vertices are partitioned into two sets and every edge has an endpoint in each set * Bipartite uterus, a type of uterus found in deer and moose, etc. * Bipartite treaty, a treaty between two parties See also * Dichotomy A dichotomy () is a partition of a set, partition of a whole (or a set) into two parts (subsets). In other words, this couple of parts must be * jointly exhaustive: everything must belong to one part or the other, and * mutually exclusive: nothi ...

Rota's Basis Conjecture
In linear algebra and matroid, matroid theory, Rota's basis conjecture is an unproven conjecture concerning rearrangements of Basis (linear algebra), bases, named after Gian-Carlo Rota. It states that, if ''X'' is either a vector space of dimension ''n'' or more generally a matroid of rank ''n'', with ''n'' disjoint bases ''Bi'', then it is possible to arrange the elements of these bases into an ''n'' × ''n'' matrix (mathematics), matrix in such a way that the rows of the matrix are exactly the given bases and the columns of the matrix are also bases. That is, it should be possible to find a second set of ''n'' disjoint bases ''Ci'', each of which consists of one element from each of the bases ''Bi''. Examples Rota's basis conjecture has a simple formulation for points in the Euclidean plane: it states that, given three triangles with distinct vertices, with each triangle colored with one of three colors, it must be possible to regroup the nine triangle vertices into thr ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]