|
Chance (philosophy)
Indeterminism is the idea that events (or certain events, or events of certain types) are not caused, or do not cause deterministically. It is the opposite of determinism and related to chance. It is highly relevant to the philosophical problem of free will, particularly in the form of libertarianism. In science, most specifically quantum theory in physics, indeterminism is the belief that no event is certain and the entire outcome of anything is probabilistic. Heisenberg's uncertainty principle and the "Born rule", proposed by Max Born, are often starting points in support of the indeterministic nature of the universe. Indeterminism is also asserted by Sir Arthur Eddington, and Murray Gell-Mann. Indeterminism has been promoted by the French biologist Jacques Monod's essay "''Chance and Necessity''". The physicist-chemist Ilya Prigogine argued for indeterminism in complex systems. Necessary but insufficient causation Indeterminists do not have to deny that causes exi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Event
Event may refer to: Gatherings of people * Ceremony, an event of ritual significance, performed on a special occasion * Convention (meeting), a gathering of individuals engaged in some common interest * Event management, the organization of events * Festival, an event that celebrates some unique aspect of a community * Happening, a type of artistic performance * Media event, an event created for publicity * Party, a social, recreational or corporate events held * Sporting event, at which athletic competition takes place * Virtual event, a gathering of individuals within a virtual environment Science, technology, and mathematics * Event (computing), a software message indicating that something has happened, such as a keystroke or mouse click * Event (philosophy), an object in time, or an instantiation of a property in an object * Event (probability theory), a set of outcomes to which a probability is assigned * Event (relativity), a point in space at an instant in time, i.e. a lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ilya Prigogine
Viscount Ilya Romanovich Prigogine (; russian: Илья́ Рома́нович Приго́жин; 28 May 2003) was a physical chemist and Nobel laureate noted for his work on dissipative structures, complex systems, and irreversibility. Biography Prigogine was born in Moscow a few months before the Russian Revolution of 1917, into a Jewish family. His father, Ruvim Abramovich Prigogine, was a chemical engineer at the Imperial Moscow Technical School; his mother, Yulia Vikhman, was a pianist. Because the family was critical of the new Soviet system, they left Russia in 1921. They first went to Germany and in 1929, to Belgium, where Prigogine received Belgian nationality in 1949. His brother Alexandre (1913–1991) became an ornithologist. Prigogine studied chemistry at the Free University of Brussels, where in 1950, he became professor. In 1959, he was appointed director of the International Solvay Institute in Brussels, Belgium. In that year, he also started teaching at the U ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomism
Atomism (from Greek , ''atomon'', i.e. "uncuttable, indivisible") is a natural philosophy proposing that the physical universe is composed of fundamental indivisible components known as atoms. References to the concept of atomism and its atoms appeared in both ancient Greek and ancient Indian philosophical traditions. Leucippus is the earliest figure whose commitment to atomism is well attested and he is usually credited with inventing atomism. He and other ancient Greek atomists theorized that nature consists of two fundamental principles: ''atom'' and ''void''. Clusters of different shapes, arrangements, and positions give rise to the various macroscopic substances in the world.Berryman, Sylvia, "Ancient Atomism", ''The Stanford Encyclopedia of Philosophy'' (Fall 2008 Edition), Edward N. Zalta (ed.)online/ref> The particles of chemical matter for which chemists and other natural philosophers of the early 19th century found experimental evidence were thought to be indivisibl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpretations Of Quantum Mechanics
An interpretation of quantum mechanics is an attempt to explain how the mathematical theory of quantum mechanics might correspond to experienced reality. Although quantum mechanics has held up to rigorous and extremely precise tests in an extraordinarily broad range of experiments, there exist a number of contending schools of thought over their interpretation. These views on interpretation differ on such fundamental questions as whether quantum mechanics is deterministic or stochastic, which elements of quantum mechanics can be considered real, and what the nature of measurement is, among other matters. Despite nearly a century of debate and experiment, no consensus has been reached among physicists and philosophers of physics concerning which interpretation best "represents" reality. History The definition of quantum theorists' terms, such as ''wave function'' and ''matrix mechanics'', progressed through many stages. For instance, Erwin Schrödinger originally viewed the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (information Theory)
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable X, which takes values in the alphabet \mathcal and is distributed according to p: \mathcal\to , 1/math>: \Eta(X) := -\sum_ p(x) \log p(x) = \mathbb \log p(X), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was introduced by Claude Shannon in his 1948 paper "A Mathematical Theory of Communication",PDF archived froherePDF archived frohere and is also referred to as Shannon entropy. Shannon's theory defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace
Pierre-Simon, marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French scholar and polymath whose work was important to the development of engineering, mathematics, statistics, physics, astronomy, and philosophy. He summarized and extended the work of his predecessors in his five-volume ''Mécanique céleste'' (''Celestial Mechanics'') (1799–1825). This work translated the geometric study of classical mechanics to one based on calculus, opening up a broader range of problems. In statistics, the Bayesian interpretation of probability was developed mainly by Laplace. Laplace formulated Laplace's equation, and pioneered the Laplace transform which appears in many branches of mathematical physics, a field that he took a leading role in forming. The Laplacian differential operator, widely used in mathematics, is also named after him. He restated and developed the nebular hypothesis of the origin of the Solar System and was one of the first scientists to suggest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Distribution Function
In probability and statistics, the quantile function, associated with a probability distribution of a random variable, specifies the value of the random variable such that the probability of the variable being less than or equal to that value equals the given probability. Intuitively, the quantile function associates with a range at and below a probability input the likelihood that a random variable is realized in that range for some probability distribution. It is also called the percentile function, percent-point function or inverse cumulative distribution function. Definition Strictly monotonic distribution function With reference to a continuous and strictly monotonic cumulative distribution function F_X\colon \mathbb \to ,1/math> of a random variable ''X'', the quantile function Q\colon , 1\to \mathbb returns a threshold value ''x'' below which random draws from the given c.d.f. would fall ''100*p'' percent of the time. In terms of the distribution function ''F'', the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of symmetric probability distributions. The distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds. The bounds are defined by the parameters, ''a'' and ''b'', which are the minimum and maximum values. The interval can either be closed (e.g. , b or open (e.g. (a, b)). Therefore, the distribution is often abbreviated ''U'' (''a'', ''b''), where U stands for uniform distribution. The difference between the bounds defines the interval length; all intervals of the same length on the distribution's support are equally probable. It is the maximum entropy probability distribution for a random variable ''X'' under no constraint other than that it is contained in the distribution's support. Definitions Probability density function The probability density function of the continuous uniform distribution is: : f(x)=\begin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a random phe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propensity Probability
The propensity theory of probability is a probability interpretation in which the probability is thought of as a physical propensity, disposition, or tendency of a given type of situation to yield an Outcome (probability), outcome of a certain kind, or to yield a long-run relative frequency of such an outcome.'Interpretations of Probability', Stanford Encyclopedia of Philosophy] Retrieved 23 December 2006. Propensities are not relative frequencies, but purported ''causes'' of the observed stable relative frequencies. Propensities are invoked to ''explain why'' repeating a certain kind of experiment will generate a given outcome type at a persistent rate. A central aspect of this explanation is the law of large numbers. This law, which is a consequence of the axioms of probability, says that if (for example) a coin is tossed repeatedly many times, in such a way that its probability of landing heads is the same on each toss, and the outcomes are probabilistically independent, then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cancer
Cancer is a group of diseases involving abnormal cell growth with the potential to invade or spread to other parts of the body. These contrast with benign tumors, which do not spread. Possible signs and symptoms include a lump, abnormal bleeding, prolonged cough, unexplained weight loss, and a change in bowel movements. While these symptoms may indicate cancer, they can also have other causes. Over 100 types of cancers affect humans. Tobacco use is the cause of about 22% of cancer deaths. Another 10% are due to obesity, poor diet, lack of physical activity or excessive drinking of alcohol. Other factors include certain infections, exposure to ionizing radiation, and environmental pollutants. In the developing world, 15% of cancers are due to infections such as ''Helicobacter pylori'', hepatitis B, hepatitis C, human papillomavirus infection, Epstein–Barr virus and human immunodeficiency virus (HIV). These factors act, at least partly, by changing the genes of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tobacco Smoking
Tobacco smoking is the practice of burning tobacco and ingesting the resulting smoke. The smoke may be inhaled, as is done with cigarettes, or simply released from the mouth, as is generally done with pipes and cigars. The practice is believed to have begun as early as 5000–3000 BC in Mesoamerica and South America. Tobacco was introduced to Eurasia in the late 17th century by European colonists, where it followed common trade routes. The practice encountered criticism from its first import into the Western world onwards but embedded itself in certain strata of a number of societies before becoming widespread upon the introduction of automated cigarette-rolling apparatus. Smoking is the most common method of consuming tobacco, and tobacco is the most common substance smoked. The agricultural product is often mixed with additives and then combusted. The resulting smoke is then inhaled and the active substances absorbed through the alveoli in the lungs or the oral mucosa. Many ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

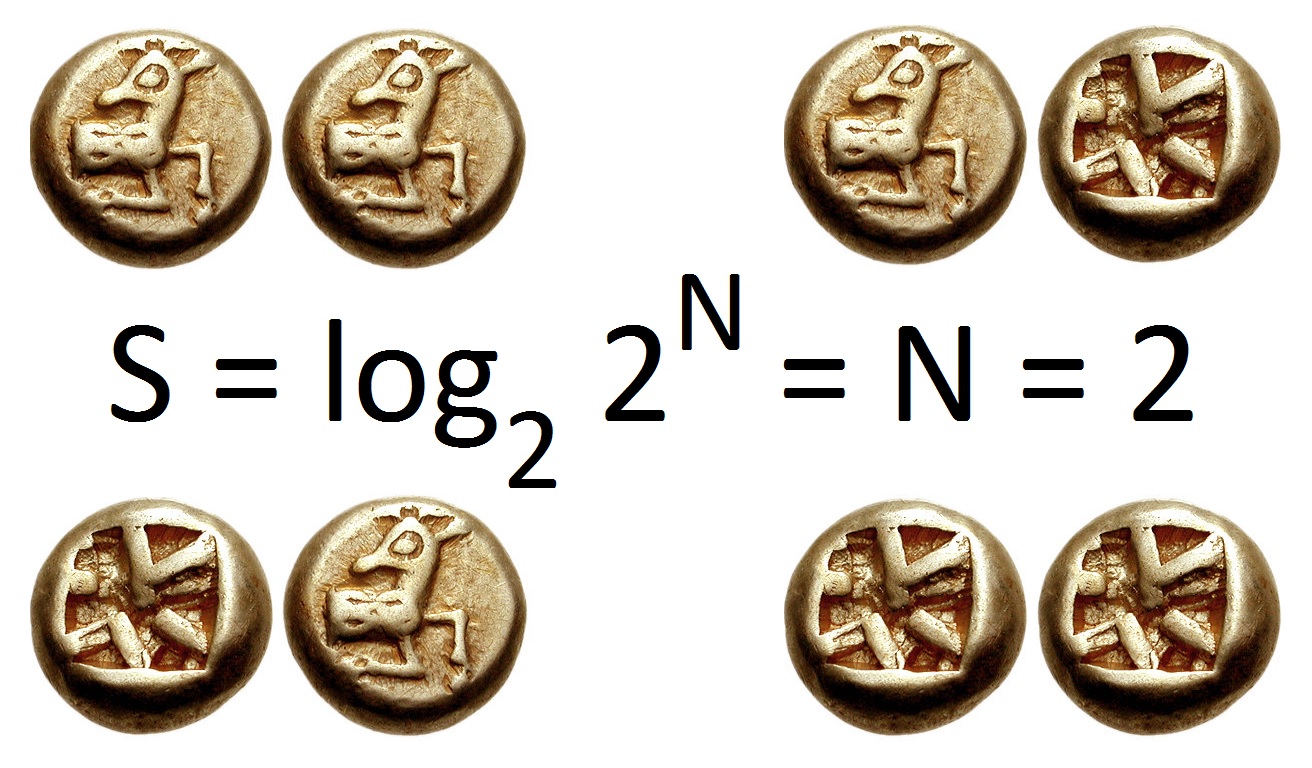
.jpg)

.jpg)