|
Canonical Commutation Relations
In quantum mechanics, the canonical commutation relation is the fundamental relation between canonical conjugate quantities (quantities which are related by definition such that one is the Fourier transform of another). For example, hat x,\hat p_x= i\hbar \mathbb between the position operator and momentum operator in the direction of a point particle in one dimension, where is the commutator of and , is the imaginary unit, and is the reduced Planck's constant , and \mathbb is the unit operator. In general, position and momentum are vectors of operators and their commutation relation between different components of position and momentum can be expressed as hat r_i,\hat p_j= i\hbar \delta_ \mathbb. where \delta_ is the Kronecker delta. This relation is attributed to Werner Heisenberg, Max Born and Pascual Jordan (1925), who called it a "quantum condition" serving as a postulate of the theory; it was noted by E. Kennard (1927) to imply the Heisenberg uncertainty pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbrand J
Hilbrand is both a given name and a surname. Notable people with the name include: * Hilbrand Boschma (1893–1976), Dutch zoologist and museum curator *Hilbrand J. Groenewold (1910–1996), Dutch theoretical physicist * Hilbrand Nawijn (born 1948), Dutch politician *Sophie Hilbrand Sophie Francine Hilbrand (born 5 October 1975) is a Dutch Television presenter, actress and radio host. She followed a course drama at De Trap, a private school for acting in Amsterdam, but left after one and a half year when she debuted on 6pack ... (born 1975), Dutch actress, television host and radio host See also * Hillebrand {{given name, type=both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heisenberg Group
In mathematics, the Heisenberg group H, named after Werner Heisenberg, is the group of 3×3 upper triangular matrices of the form ::\begin 1 & a & c\\ 0 & 1 & b\\ 0 & 0 & 1\\ \end under the operation of matrix multiplication. Elements ''a, b'' and ''c'' can be taken from any commutative ring with identity, often taken to be the ring of real numbers (resulting in the "continuous Heisenberg group") or the ring of integers (resulting in the "discrete Heisenberg group"). The continuous Heisenberg group arises in the description of one-dimensional quantum mechanical systems, especially in the context of the Stone–von Neumann theorem. More generally, one can consider Heisenberg groups associated to ''n''-dimensional systems, and most generally, to any symplectic vector space. The three-dimensional case In the three-dimensional case, the product of two Heisenberg matrices is given by: :\begin 1 & a & c\\ 0 & 1 & b\\ 0 & 0 & 1\\ \end \begin 1 & a' & c'\\ 0 & 1 & b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi identity. The Lie bracket of two vectors x and y is denoted ,y/math>. The vector space \mathfrak g together with this operation is a non-associative algebra, meaning that the Lie bracket is not necessarily associative. Lie algebras are closely related to Lie groups, which are groups that are also smooth manifolds: any Lie group gives rise to a Lie algebra, which is its tangent space at the identity. Conversely, to any finite-dimensional Lie algebra over real or complex numbers, there is a corresponding connected Lie group unique up to finite coverings ( Lie's third theorem). This correspondence allows one to study the structure and classification of Lie groups in terms of Lie algebras. In physics, Lie groups appear as symmetry grou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Map (Lie Theory)
In the theory of Lie groups, the exponential map is a map from the Lie algebra \mathfrak g of a Lie group G to the group, which allows one to recapture the local group structure from the Lie algebra. The existence of the exponential map is one of the primary reasons that Lie algebras are a useful tool for studying Lie groups. The ordinary exponential function of mathematical analysis is a special case of the exponential map when G is the multiplicative group of positive real numbers (whose Lie algebra is the additive group of all real numbers). The exponential map of a Lie group satisfies many properties analogous to those of the ordinary exponential function, however, it also differs in many important respects. Definitions Let G be a Lie group and \mathfrak g be its Lie algebra (thought of as the tangent space to the identity element of G). The exponential map is a map :\exp\colon \mathfrak g \to G which can be defined in several different ways. The typical modern definition i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Group
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additional properties it must have to be thought of as a "transformation" in the abstract sense, for instance multiplication and the taking of inverses (division), or equivalently, the concept of addition and the taking of inverses (subtraction). Combining these two ideas, one obtains a continuous group where multiplying points and their inverses are continuous. If the multiplication and taking of inverses are smooth (differentiable) as well, one obtains a Lie group. Lie groups provide a natural model for the concept of continuous symmetry, a celebrated example of which is the rotational symmetry in three dimensions (given by the special orthogonal group \text(3)). Lie groups are widely used in many parts of modern mathematics and physics. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Derivative
In the calculus of variations, a field of mathematical analysis, the functional derivative (or variational derivative) relates a change in a functional (a functional in this sense is a function that acts on functions) to a change in a function on which the functional depends. In the calculus of variations, functionals are usually expressed in terms of an integral of functions, their arguments, and their derivatives. In an integral of a functional, if a function is varied by adding to it another function that is arbitrarily small, and the resulting integrand is expanded in powers of , the coefficient of in the first order term is called the functional derivative. For example, consider the functional J = \int_a^b L( \, x, f(x), f \, '(x) \, ) \, dx \ , where . If is varied by adding to it a function , and the resulting integrand is expanded in powers of , then the change in the value of to first order in can be expressed as follows:According to , this notation is custo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heisenberg Picture
In physics, the Heisenberg picture (also called the Heisenberg representation) is a formulation (largely due to Werner Heisenberg in 1925) of quantum mechanics in which the operators ( observables and others) incorporate a dependency on time, but the state vectors are time-independent, an arbitrary fixed basis rigidly underlying the theory. It stands in contrast to the Schrödinger picture in which the operators are constant, instead, and the states evolve in time. The two pictures only differ by a basis change with respect to time-dependency, which corresponds to the difference between active and passive transformations. The Heisenberg picture is the formulation of matrix mechanics in an arbitrary basis, in which the Hamiltonian is not necessarily diagonal. It further serves to define a third, hybrid, picture, the interaction picture. Mathematical details In the Heisenberg picture of quantum mechanics the state vectors , ''ψ''⟩ do not change with time, while observab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schrödinger Equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933. Conceptually, the Schrödinger equation is the quantum counterpart of Newton's second law in classical mechanics. Given a set of known initial conditions, Newton's second law makes a mathematical prediction as to what path a given physical system will take over time. The Schrödinger equation gives the evolution over time of a wave function, the quantum-mechanical characterization of an isolated physical system. The equation can be derived from the fact that the time-evolution operator must be unitary, and must therefore be generated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correspondence Principle
In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics (or by the old quantum theory) reproduces classical physics in the limit of large quantum numbers. In other words, it says that for large orbits and for large energies, quantum calculations must agree with classical calculations. The principle was formulated by Niels Bohr in 1920, though he had previously made use of it as early as 1913 in developing his model of the atom. The term codifies the idea that a new theory should reproduce under some conditions the results of older well-established theories in those domains where the old theories work. This concept is somewhat different from the requirement of a formal limit under which the new theory reduces to the older, thanks to the existence of a deformation parameter. Classical quantities appear in quantum mechanics in the form of expected values of observables, and as such the Ehrenfest theorem (whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
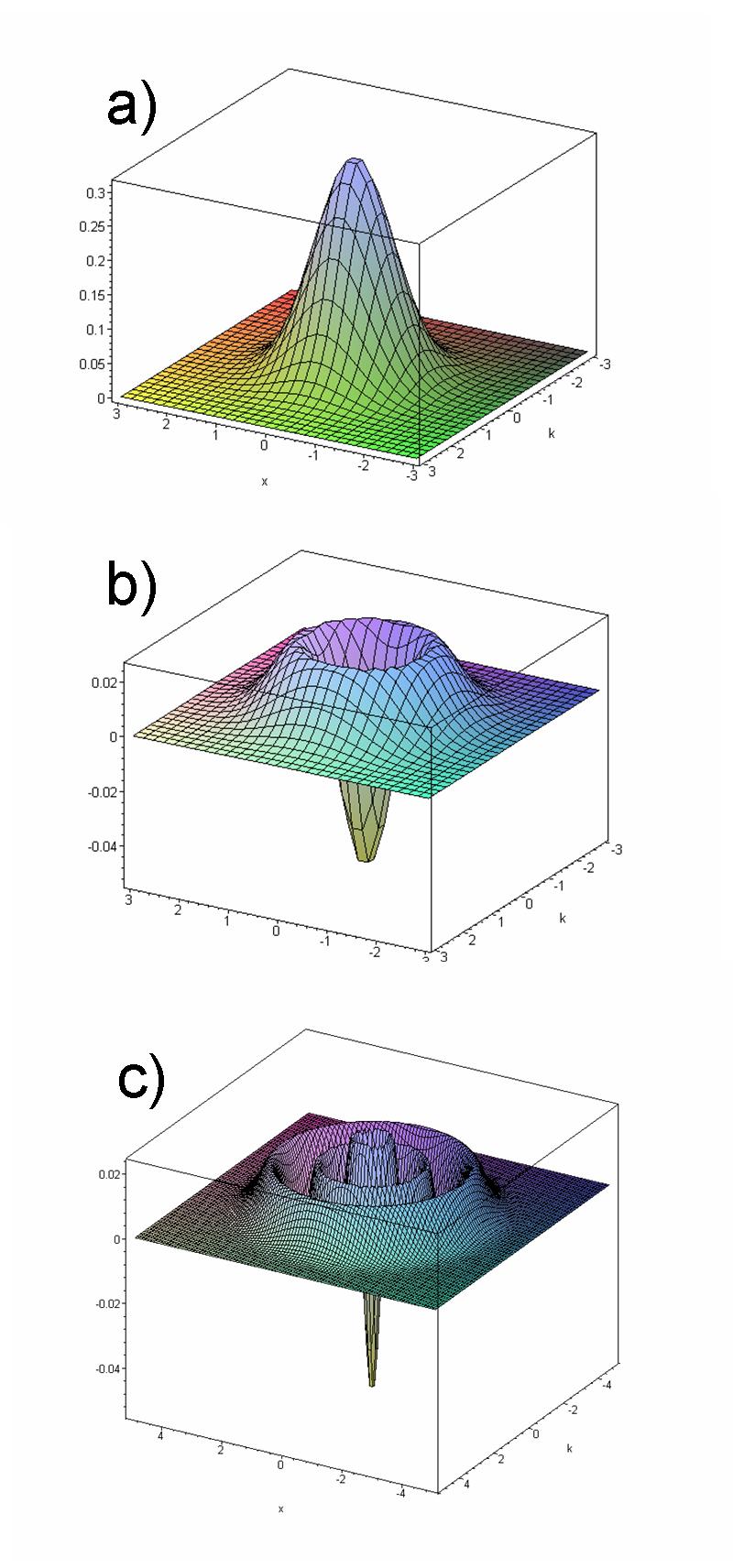
Phase-space Formulation
The phase-space formulation of quantum mechanics places the position ''and'' momentum variables on equal footing in phase space. In contrast, the Schrödinger picture uses the position ''or'' momentum representations (see also position and momentum space). The two key features of the phase-space formulation are that the quantum state is described by a quasiprobability distribution (instead of a wave function, state vector, or density matrix) and operator multiplication is replaced by a star product. The theory was fully developed by Hilbrand Groenewold in 1946 in his PhD thesis, and independently by Joe Moyal, each building on earlier ideas by Hermann Weyl and Eugene Wigner. The chief advantage of the phase-space formulation is that it makes quantum mechanics appear as similar to Hamiltonian mechanics as possible by avoiding the operator formalism, thereby "'freeing' the quantization of the 'burden' of the Hilbert space". This formulation is statistical in nature and of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wigner–Weyl Transform
In quantum mechanics, the Wigner–Weyl transform or Weyl–Wigner transform (after Hermann Weyl and Eugene Wigner) is the invertible mapping between functions in the quantum phase space formulation and Hilbert space operators in the Schrödinger picture. Often the mapping from functions on phase space to operators is called the Weyl transform or Weyl quantization, whereas the inverse mapping, from operators to functions on phase space, is called the Wigner transform. This mapping was originally devised by Hermann Weyl in 1927 in an attempt to map symmetrized ''classical'' phase space functions to operators, a procedure known as ''Weyl quantization''. It is now understood that Weyl quantization does not satisfy all the properties one would require for consistent quantization and therefore sometimes yields unphysical answers. On the other hand, some of the nice properties described below suggest that if one seeks a single consistent procedure mapping functions on the classica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |



.png)