|
Functional Derivative
In the calculus of variations, a field of mathematical analysis, the functional derivative (or variational derivative) relates a change in a functional (a functional in this sense is a function that acts on functions) to a change in a function on which the functional depends. In the calculus of variations, functionals are usually expressed in terms of an integral of functions, their arguments, and their derivatives. In an integrand of a functional, if a function is varied by adding to it another function that is arbitrarily small, and the resulting integrand is expanded in powers of , the coefficient of in the first order term is called the functional derivative. For example, consider the functional J = \int_a^b L( \, x, f(x), f' \, ) \, dx \, , where . If is varied by adding to it a function , and the resulting integrand is expanded in powers of , then the change in the value of to first order in can be expressed as follows:According to , this notation is customary in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Calculus Of Variations
The calculus of variations (or variational calculus) is a field of mathematical analysis that uses variations, which are small changes in Function (mathematics), functions and functional (mathematics), functionals, to find maxima and minima of functionals: Map (mathematics), mappings from a set of Function (mathematics), functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points. If there are no constraints, the solution is a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as ''geodesics''. A related problem is posed by Fermat's principle: li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Principle Of Least Action
Action principles lie at the heart of fundamental physics, from classical mechanics through quantum mechanics, particle physics, and general relativity. Action principles start with an energy function called a Lagrangian describing the physical system. The accumulated value of this energy function between two states of the system is called the action. Action principles apply the calculus of variation to the action. The action depends on the energy function, and the energy function depends on the position, motion, and interactions in the system: variation of the action allows the derivation of the equations of motion without vectors or forces. Several distinct action principles differ in the constraints on their initial and final conditions. The names of action principles have evolved over time and differ in details of the endpoints of the paths and the nature of the variation. Quantum action principles generalize and justify the older classical principles by showing they are a di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
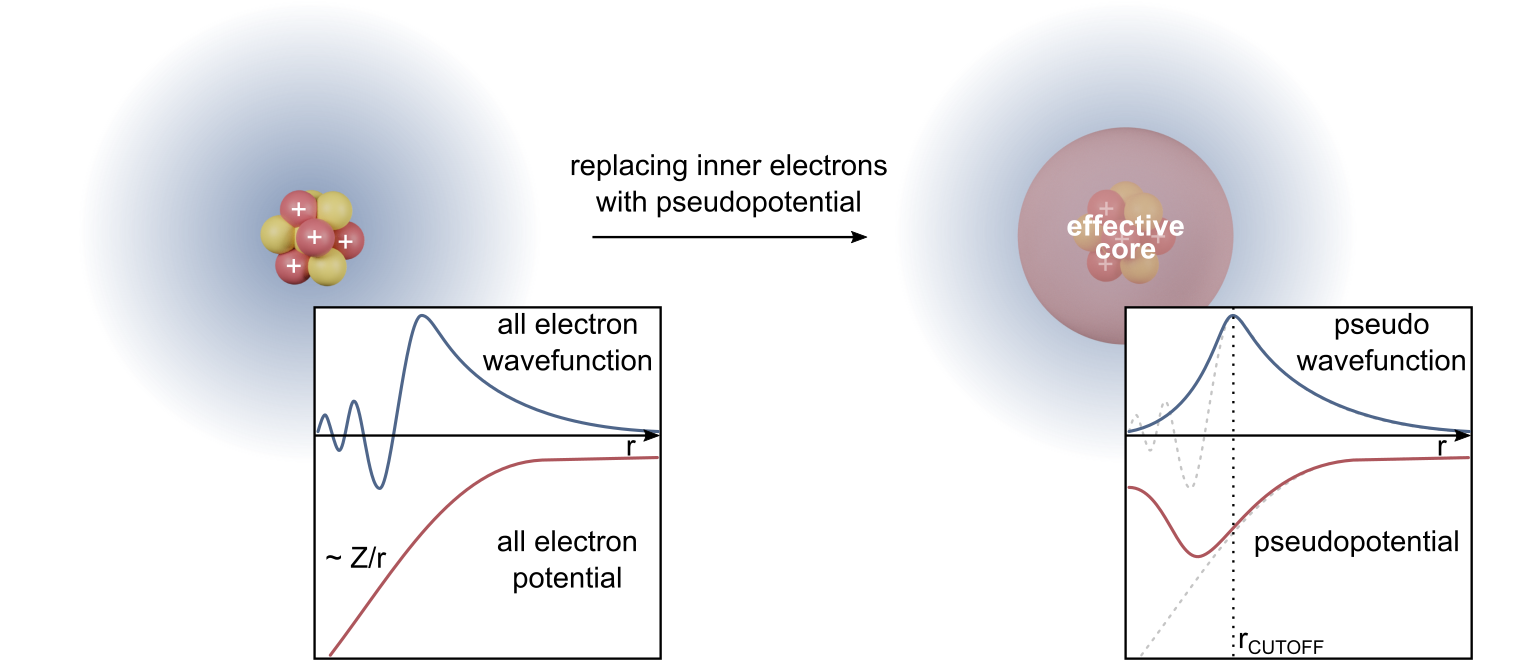
Density-functional Theory
Density functional theory (DFT) is a computational quantum mechanics, quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure (or nuclear structure) (principally the ground state) of Many-body problem, many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using Functional (mathematics), functionals - that is, functions that accept a function as input and output a single real number. In the case of DFT, these are functionals of the spatially dependent electronic density, electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry. DFT has been very popular for calculations in solid-state physics since the 1970s. However, DFT was not considered accurate enough for calculations in quantum chemistry until the 1990 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Free Electron Model
In solid-state physics, the free electron model is a quantum mechanical model for the behaviour of charge carriers in a metallic solid. It was developed in 1927, principally by Arnold Sommerfeld, who combined the classical Drude model with quantum mechanical Fermi–Dirac statistics and hence it is also known as the Drude–Sommerfeld model. Given its simplicity, it is surprisingly successful in explaining many experimental phenomena, especially * the Wiedemann–Franz law which relates electrical conductivity and thermal conductivity; * the temperature dependence of the electron heat capacity; * the shape of the electronic density of states; * the range of binding energy values; * electrical conductivities; * the Seebeck coefficient of the thermoelectric effect; * thermal electron emission and field electron emission from bulk metals. The free electron model solved many of the inconsistencies related to the Drude model and gave insight into several other properties of me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Thomas–Fermi Model
The Thomas–Fermi (TF) model, named after Llewellyn Thomas and Enrico Fermi, is a quantum mechanical theory for the electronic structure of many-body systems developed semiclassically shortly after the introduction of the Schrödinger equation. It stands separate from wave function theory as being formulated in terms of the electronic density alone and as such is viewed as a precursor to modern density functional theory. The Thomas–Fermi model is correct only in the limit of an infinite nuclear charge. Using the approximation for realistic systems yields poor quantitative predictions, even failing to reproduce some general features of the density such as shell structure in atoms and Friedel oscillations in solids. It has, however, found modern applications in many fields through the ability to extract qualitative trends analytically and with the ease at which the model can be solved. The kinetic energy expression of Thomas–Fermi theory is also used as a component in mor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Coulomb Potential Energy Functional
The coulomb (symbol: C) is the unit of electric charge in the International System of Units (SI). It is defined to be equal to the electric charge delivered by a 1 ampere current in 1 second, with the elementary charge ''e'' as a defining constant in the SI. Definition The SI defines the coulomb as "the quantity of electricity carried in 1 second by a current of 1 ampere" by fixing the value of the elementary charge, . Inverting the relationship, the coulomb can be expressed in terms of the elementary charge: 1 ~ \mathrm = \frac = \frac ~ e. It is approximately and is thus not an integer multiple of the elementary charge. The coulomb was previously defined in terms of the ampere based on the force between two wires, as . The 2019 redefinition of the ampere and other SI base units fixed the numerical value of the elementary charge when expressed in coulombs and therefore fixed the value of the coulomb when expressed as a multiple of the fundamental charge. SI prefixe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fundamental Lemma Of Calculus Of Variations
In mathematics, specifically in the calculus of variations, a variation of a function can be concentrated on an arbitrarily small interval, but not a single point. Accordingly, the necessary condition of extremum (functional derivative equal zero) appears in a weak formulation (variational form) integrated with an arbitrary function . The fundamental lemma of the calculus of variations is typically used to transform this weak formulation into the strong formulation ( differential equation), free of the integration with arbitrary function. The proof usually exploits the possibility to choose concentrated on an interval on which keeps sign (positive or negative). Several versions of the lemma are in use. Basic versions are easy to formulate and prove. More powerful versions are used when needed. Basic version :If a continuous function f on an open interval (a,b) satisfies the equality :: \int_a^b f(x)h(x)\,\mathrmx = 0 :for all compactly supported smooth functions h on (a,b), th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Divergence Theorem
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, reprinted in is a theorem relating the '' flux'' of a vector field through a closed surface to the ''divergence'' of the field in the volume enclosed. More precisely, the divergence theorem states that the surface integral of a vector field over a closed surface, which is called the "flux" through the surface, is equal to the volume integral of the divergence over the region enclosed by the surface. Intuitively, it states that "the sum of all sources of the field in a region (with sinks regarded as negative sources) gives the net flux out of the region". The divergence theorem is an important result for the mathematics of physics and engineering, particularly in electrostatics and fluid dynamics. In these fields, it is usually applied in three dimensions. However, it generalizes to any number of dimensions. In one dimension, it is equivalent to the fundamental theorem of cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to area.) More precisely, the divergence at a point is the rate that the flow of the vector field modifies a volume about the point ''in the limit'', as a small volume shrinks down to the point. As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value. Physical interpretation of divergence In physical terms, the divergence of a vector field is the extent to which the vector fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Matrix Calculus
In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrix (mathematics), matrices. It collects the various partial derivatives of a single Function (mathematics), function with respect to many Variable (mathematics), variables, and/or of a multivariate function with respect to a single variable, into Vector (mathematics and physics), vectors and matrices that can be treated as single entities. This greatly simplifies operations such as finding the maximum or minimum of a multivariate function and solving systems of differential equations. The notation used here is commonly used in statistics and engineering, while the tensor index notation is preferred in physics. Two competing notational conventions split the field of matrix calculus into two separate groups. The two groups can be distinguished by whether they write the derivative of a Scalar (mathematics), scalar with respect to a vector as a Row and column ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Total Derivative
In mathematics, the total derivative of a function at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with respect to all of its arguments, not just a single one. In many situations, this is the same as considering all partial derivatives simultaneously. The term "total derivative" is primarily used when is a function of several variables, because when is a function of a single variable, the total derivative is the same as the ordinary derivative of the function. The total derivative as a linear map Let U \subseteq \R^n be an open subset. Then a function f:U \to \R^m is said to be (totally) differentiable at a point a\in U if there exists a linear transformation df_a:\R^n \to \R^m such that :\lim_ \frac=0. The linear map df_a is called the (total) derivative or (total) differential of f at a. Other notations for the total derivative inc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Definition
A definition is a statement of the meaning of a term (a word, phrase, or other set of symbols). Definitions can be classified into two large categories: intensional definitions (which try to give the sense of a term), and extensional definitions (which try to list the objects that a term describes).Lyons, John. "Semantics, vol. I." Cambridge: Cambridge (1977). p.158 and on. Another important category of definitions is the class of ostensive definitions, which convey the meaning of a term by pointing out examples. A term may have many different senses and multiple meanings, and thus require multiple definitions. In mathematics, a definition is used to give a precise meaning to a new term, by describing a condition which unambiguously qualifies what the mathematical term is and is not. Definitions and axioms form the basis on which all of modern mathematics is to be constructed. Basic terminology In modern usage, a definition is something, typically expressed in words, that at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |