|
Crack Closure
Crack closure is a phenomenon in fatigue loading, where the opposing faces of a crack remain in contact even with an external load acting on the material. As the load is increased, a critical value will be reached at which time the crack becomes ''open''. Crack closure occurs from the presence of material propping open the crack faces and can arise from many sources including plastic deformation or phase transformation during crack propagation, corrosion of crack surfaces, presence of fluids in the crack, or roughness at cracked surfaces. Description During cyclic loading, a crack will open and close causing the crack tip opening displacement (CTOD) to vary cyclically in phase with the applied force. If the loading cycle includes a period of negative force or stress ratio R (i.e. R < 0), the CTOD will remain equal to zero as the crack faces are pressed together. However, it was discovered that the CTOD can also be zero at other times even when the applied force is posi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fatigue (material)
In materials science, fatigue is the initiation and propagation of cracks in a material due to cyclic loading. Once a fatigue crack has initiated, it grows a small amount with each loading cycle, typically producing striations on some parts of the fracture surface. The crack will continue to grow until it reaches a critical size, which occurs when the stress intensity factor of the crack exceeds the fracture toughness of the material, producing rapid propagation and typically complete fracture of the structure. Fatigue has traditionally been associated with the failure of metal components which led to the term metal fatigue. In the nineteenth century, the sudden failing of metal railway axles was thought to be caused by the metal ''crystallising'' because of the brittle appearance of the fracture surface, but this has since been disproved. Most materials, such as composites, plastics and ceramics, seem to experience some sort of fatigue-related failure. To aid in predicting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane Strain
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller (indeed, infinitesimally smaller) than any relevant dimension of the body; so that its geometry and the constitutive properties of the material (such as density and stiffness) at each point of space can be assumed to be unchanged by the deformation. With this assumption, the equations of continuum mechanics are considerably simplified. This approach may also be called small deformation theory, small displacement theory, or small displacement-gradient theory. It is contrasted with the finite strain theory where the opposite assumption is made. The infinitesimal strain theory is commonly adopted in civil and mechanical engineering for the stress analysis of structures built from relatively stiff elastic materials like concrete and steel, since a common go ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anisotropy
Anisotropy () is the property of a material which allows it to change or assume different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties ( absorbance, refractive index, conductivity, tensile strength, etc.). An example of anisotropy is light coming through a polarizer. Another is wood, which is easier to split along its grain than across it. Fields of interest Computer graphics In the field of computer graphics, an anisotropic surface changes in appearance as it rotates about its geometric normal, as is the case with velvet. Anisotropic filtering (AF) is a method of enhancing the image quality of textures on surfaces that are far away and steeply angled with respect to the point of view. Older techniques, such as bilinear and trilinear filtering, do not take into account the angle a surface is viewed from, which can result in alias ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fracture Mechanics
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture. Theoretically, the stress ahead of a sharp crack tip becomes infinite and cannot be used to describe the state around a crack. Fracture mechanics is used to characterise the loads on a crack, typically using a single parameter to describe the complete loading state at the crack tip. A number of different parameters have been developed. When the plastic zone at the tip of the crack is small relative to the crack length the stress state at the crack tip is the result of elastic forces within the material and is termed linear elastic fracture mechanics (LEFM) and can be characterised using the stress intensity factor K. Although the load on a crack can be arbitrary, in 1957 G. Irwin f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Redox
Redox (reduction–oxidation, , ) is a type of chemical reaction in which the oxidation states of substrate change. Oxidation is the loss of electrons or an increase in the oxidation state, while reduction is the gain of electrons or a decrease in the oxidation state. There are two classes of redox reactions: * ''Electron-transfer'' – Only one (usually) electron flows from the reducing agent to the oxidant. This type of redox reaction is often discussed in terms of redox couples and electrode potentials. * ''Atom transfer'' – An atom transfers from one substrate to another. For example, in the rusting of iron, the oxidation state of iron atoms increases as the iron converts to an oxide, and simultaneously the oxidation state of oxygen decreases as it accepts electrons released by the iron. Although oxidation reactions are commonly associated with the formation of oxides, other chemical species can serve the same function. In hydrogenation, C=C (and other) bonds are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martensite
Martensite is a very hard form of steel crystalline structure. It is named after German metallurgist Adolf Martens. By analogy the term can also refer to any crystal structure that is formed by diffusionless transformation. Properties Martensite is formed in carbon steels by the rapid cooling ( quenching) of the austenite form of iron at such a high rate that carbon atoms do not have time to diffuse out of the crystal structure in large enough quantities to form cementite (Fe3C). Austenite is gamma-phase iron (γ-Fe), a solid solution of iron and alloying elements. As a result of the quenching, the face-centered cubic austenite transforms to a highly strained body-centered tetragonal form called martensite that is supersaturated with carbon. The shear deformations that result produce a large number of dislocations, which is a primary strengthening mechanism of steels. The highest hardness of a pearlitic steel is 400 Brinell, whereas martensite can achieve 700&n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Austenite
Austenite, also known as gamma-phase iron (γ-Fe), is a metallic, non-magnetic allotrope of iron or a solid solution of iron with an alloying element. In plain-carbon steel, austenite exists above the critical eutectoid temperature of 1000 K (727 °C); other alloys of steel have different eutectoid temperatures. The austenite allotrope is named after Sir William Chandler Roberts-Austen (1843–1902); it exists at room temperature in some stainless steels due to the presence of nickel stabilizing the austenite at lower temperatures. Allotrope of iron From alpha iron undergoes a phase transition from body-centered cubic (BCC) to the face-centered cubic (FCC) configuration of gamma iron, also called austenite. This is similarly soft and ductile but can dissolve considerably more carbon (as much as 2.03% by mass at ). This gamma form of iron is present in the most commonly used type of stainless steel for making hospital and food-service equipment. Material Austeniti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane Stress
In continuum mechanics, a material is said to be under plane stress if the stress vector is zero across a particular plane. When that situation occurs over an entire element of a structure, as is often the case for thin plates, the stress analysis is considerably simplified, as the stress state can be represented by a tensor of dimension 2 (representable as a 2×2 matrix rather than 3×3). A related notion, plane strain, is often applicable to very thick members. Plane stress typically occurs in thin flat plates that are acted upon only by load forces that are parallel to them. In certain situations, a gently curved thin plate may also be assumed to have plane stress for the purpose of stress analysis. This is the case, for example, of a thin-walled cylinder filled with a fluid under pressure. In such cases, stress components perpendicular to the plate are negligible compared to those parallel to it. In other situations, however, the bending stress of a thin plate cannot be ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
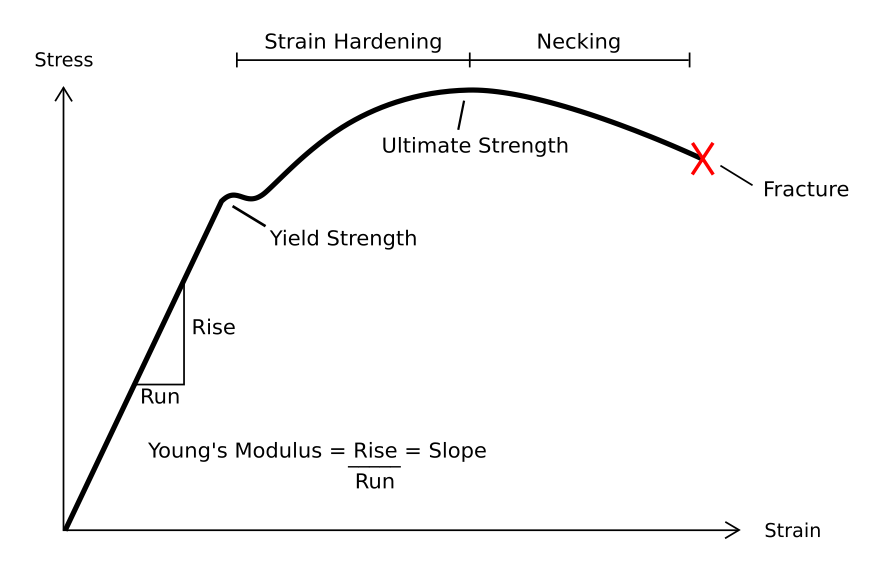
Plastic Deformation
In engineering, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain is the ''relative'' internal change in shape of an infinitesimally small cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is elastic. The linear relationship for a material is known as Young's modulus. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials and for a st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crack Growth Equation
A crack growth equation is used for calculating the size of a fatigue crack growing from cyclic loads. The growth of fatigue cracks can result in catastrophic failure, particularly in the case of aircraft. A crack growth equation can be used to ensure safety, both in the design phase and during operation, by predicting the size of cracks. In critical structure, loads can be recorded and used to predict the size of cracks to ensure maintenance or retirement occurs prior to any of the cracks failing. ''Fatigue life'' can be divided into an initiation period and a crack growth period. Crack growth equations are used to predict the crack size starting from a given initial flaw and are typically based on experimental data obtained from constant amplitude fatigue tests. One of the earliest crack growth equations based on the stress intensity factor range of a load cycle (\Delta K) is the Paris–Erdogan equation. : = C(\Delta K)^m where a is the crack length and a/N is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress Intensity Factor
In fracture mechanics, the stress intensity factor () is used to predict the stress state ("stress intensity") near the tip of a crack or notch caused by a remote load or residual stresses. It is a theoretical construct usually applied to a homogeneous, linear elastic material and is useful for providing a failure criterion for brittle materials, and is a critical technique in the discipline of damage tolerance. The concept can also be applied to materials that exhibit ''small-scale yielding'' at a crack tip. The magnitude of depends on specimen geometry, the size and location of the crack or notch, and the magnitude and the distribution of loads on the material. It can be written as: :K = \sigma \sqrt \, f(a/W) where f(a/W) is a specimen geometry dependent function of the crack length, , and the specimen width, , and is the applied stress. Linear elastic theory predicts that the stress distribution (\sigma_) near the crack tip, in polar coordinates (r,\theta) with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |