|
Coskewness
In probability theory and statistics, coskewness is a measure of how much three random variables change together. Coskewness is the third standardized cross central moment, related to skewness as covariance is related to variance. In 1976, Krauss and Litzenberger used it to examine risk in stock market investments. The application to risk was extended by Harvey and Siddique in 2000. If three random variables exhibit positive coskewness they will tend to undergo extreme deviations at the same time, an odd number of which are in the positive direction (so all three random variables undergoing extreme positive deviations, or one undergoing an extreme positive deviation while the other two undergo extreme negative deviations). Similarly, if three random variables exhibit negative coskewness they will tend to undergo extreme deviations at the same time, an even number of which are in the positive direction (so all three random variables undergoing extreme negative deviations, or one under ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cokurtosis
In probability theory and statistics, cokurtosis is a measure of how much two random variables change together. Cokurtosis is the fourth standardized cross central moment. If two random variables exhibit a high level of cokurtosis they will tend to undergo extreme positive and negative deviations at the same time. Definition For two random variables ''X'' and ''Y'' there are three non-trivial cokurtosis statistics : K(X,X,X,Y) = , : K(X,X,Y,Y) = , and : K(X,Y,Y,Y) = , where E 'X''is the expected value of ''X'', also known as the mean of ''X'', and \sigma_X is the standard deviation of ''X''. Properties * Kurtosis is a special case of the cokurtosis when the two random variables are identical: :: K(X,X,X,X) = = , * For two random variables, ''X'' and ''Y'', the kurtosis of the sum, ''X'' + ''Y'', is :: \begin K_ = \big & \sigma_X^4K_X + 4\sigma_X^3\sigma_YK(X,X,X,Y) + 6\sigma_X^2\sigma_Y^2K(X,X,Y,Y) \\ & + 4\sigma_X\sigma_Y^3K(X,Y,Y,Y) + \sigma_Y^4K_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
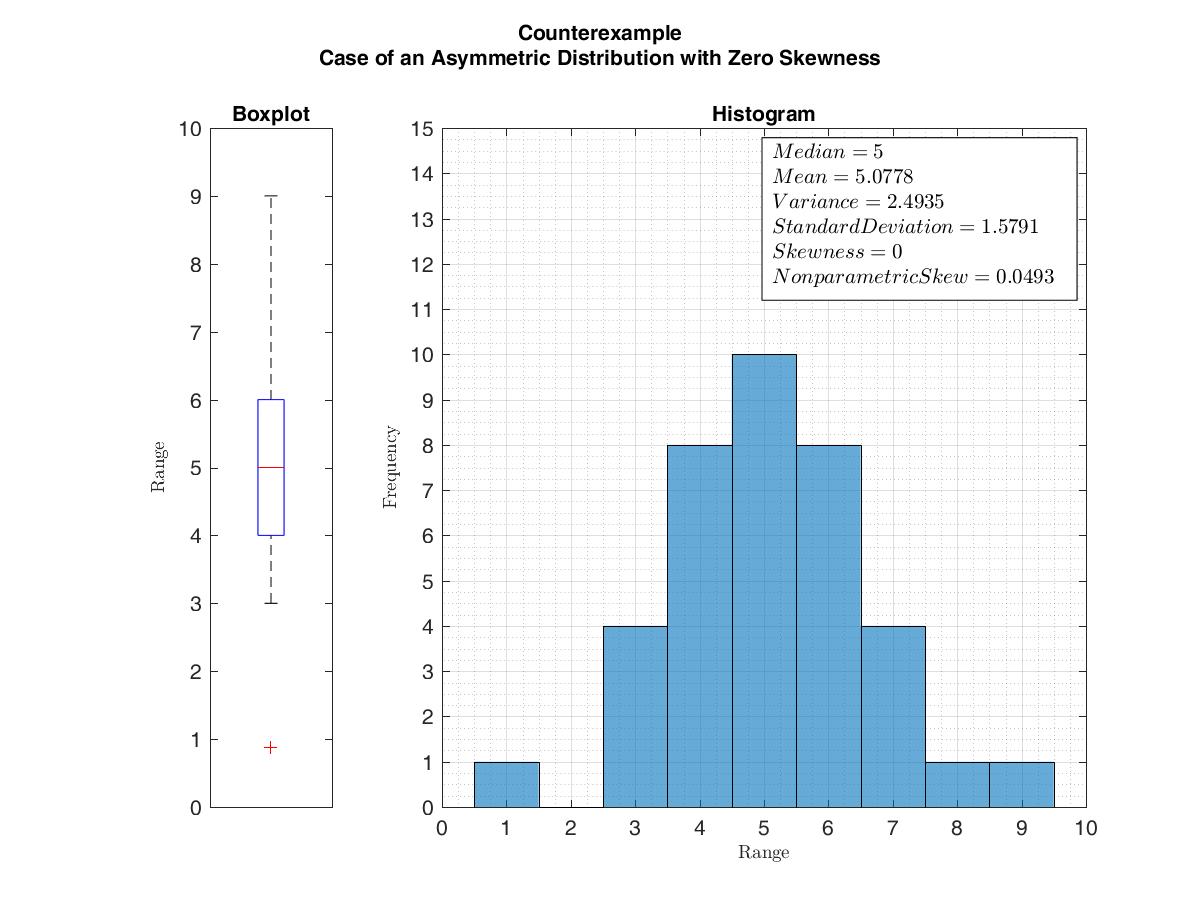
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined. For a unimodal distribution, negative skew commonly indicates that the ''tail'' is on the left side of the distribution, and positive skew indicates that the tail is on the right. In cases where one tail is long but the other tail is fat, skewness does not obey a simple rule. For example, a zero value means that the tails on both sides of the mean balance out overall; this is the case for a symmetric distribution, but can also be true for an asymmetric distribution where one tail is long and thin, and the other is short but fat. Introduction Consider the two distributions in the figure just below. Within each graph, the values on the right side of the distribution taper differently from the values on the left side. These tapering sides are called ''tai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined. For a unimodal distribution, negative skew commonly indicates that the ''tail'' is on the left side of the distribution, and positive skew indicates that the tail is on the right. In cases where one tail is long but the other tail is fat, skewness does not obey a simple rule. For example, a zero value means that the tails on both sides of the mean balance out overall; this is the case for a symmetric distribution, but can also be true for an asymmetric distribution where one tail is long and thin, and the other is short but fat. Introduction Consider the two distributions in the figure just below. Within each graph, the values on the right side of the distribution taper differently from the values on the left side. These tapering sides are called ''tai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of non-deterministic or uncertain processes or measured quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly predict random events, much can be said about their behavior. Two major results in probab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra Of Random Variables
The algebra of random variables in statistics, provides rules for the symbolic manipulation of random variables, while avoiding delving too deeply into the mathematically sophisticated ideas of probability theory. Its symbolism allows the treatment of sums, products, ratios and general functions of random variables, as well as dealing with operations such as finding the probability distributions and the expectations (or expected values), variances and covariances of such combinations. In principle, the elementary algebra of random variables is equivalent to that of conventional non-random (or deterministic) variables. However, the changes occurring on the probability distribution of a random variable obtained after performing algebraic operations are not straightforward. Therefore, the behavior of the different operators of the probability distribution, such as expected values, variances, covariances, and moments, may be different from that observed for the random variable u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment (mathematics)
In mathematics, the moments of a function are certain quantitative measures related to the shape of the function's graph. If the function represents mass density, then the zeroth moment is the total mass, the first moment (normalized by total mass) is the center of mass, and the second moment is the moment of inertia. If the function is a probability distribution, then the first moment is the expected value, the second central moment is the variance, the third standardized moment is the skewness, and the fourth standardized moment is the kurtosis. The mathematical concept is closely related to the concept of moment in physics. For a distribution of mass or probability on a bounded interval, the collection of all the moments (of all orders, from to ) uniquely determines the distribution ( Hausdorff moment problem). The same is not true on unbounded intervals ( Hamburger moment problem). In the mid-nineteenth century, Pafnuty Chebyshev became the first person to think syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Delta Function
In mathematics, the Dirac delta distribution ( distribution), also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. The current understanding of the unit impulse is as a linear functional that maps every continuous function (e.g., f(x)) to its value at zero of its domain (f(0)), or as the weak limit of a sequence of bump functions (e.g., \delta(x) = \lim_ \frace^), which are zero over most of the real line, with a tall spike at the origin. Bump functions are thus sometimes called "approximate" or "nascent" delta distributions. The delta function was introduced by physicist Paul Dirac as a tool for the normalization of state vectors. It also has uses in probability theory and signal processing. Its validity was disputed until Laurent Schwartz developed the theory of distributions where it is defined as a linear form actin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heaviside Step Function
The Heaviside step function, or the unit step function, usually denoted by or (but sometimes , or ), is a step function, named after Oliver Heaviside (1850–1925), the value of which is zero for negative arguments and one for positive arguments. It is an example of the general class of step functions, all of which can be represented as linear combinations of translations of this one. The function was originally developed in operational calculus for the solution of differential equations, where it represents a signal that switches on at a specified time and stays switched on indefinitely. Oliver Heaviside, who developed the operational calculus as a tool in the analysis of telegraphic communications, represented the function as . The Heaviside function may be defined as: * a piecewise function: H(x) := \begin 1, & x > 0 \\ 0, & x \le 0 \end * using the Iverson bracket notation: H(x) := 0.html" ;"title=">0">>0/math> * an indicator function: H(x) := \mathbf_=\mathbf 1_(x ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Half-normal Distribution
In probability theory and statistics, the half-normal distribution is a special case of the folded normal distribution. Let X follow an ordinary normal distribution, N(0,\sigma^2). Then, Y=, X, follows a half-normal distribution. Thus, the half-normal distribution is a fold at the mean of an ordinary normal distribution with mean zero. Properties Using the \sigma parametrization of the normal distribution, the probability density function (PDF) of the half-normal is given by : f_Y(y; \sigma) = \frac\exp \left( -\frac \right) \quad y \geq 0, where E = \mu = \frac. Alternatively using a scaled precision (inverse of the variance) parametrization (to avoid issues if \sigma is near zero), obtained by setting \theta=\frac, the probability density function is given by : f_Y(y; \theta) = \frac\exp \left( -\frac \right) \quad y \geq 0, where E = \mu = \frac. The cumulative distribution function (CDF) is given by : F_Y(y; \sigma) = \int_0^y \frac\sqrt \, \exp \left( -\frac \rig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. Standard deviation may be abbreviated SD, and is most commonly represented in mathematical texts and equations by the lower case Greek letter σ (sigma), for the population standard deviation, or the Latin letter '' s'', for the sample standard deviation. The standard deviation of a random variable, sample, statistical population, data set, or probability distribution is the square root of its variance. It is algebraically simpler, though in practice less robust, than the average absolute deviation. A useful property of the standard deviation is that, unlike the variance, it is expressed in the same unit as the data. The standard deviation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with also often stylized as or \mathbb. History The idea of the expected value originated in the middle of the 17th century from the study of the so-called problem of points, which seeks to divide the stakes ''in a fair way'' between two players, who have to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |