|
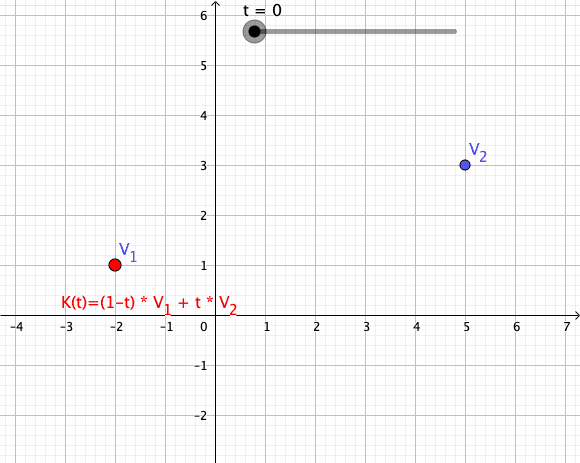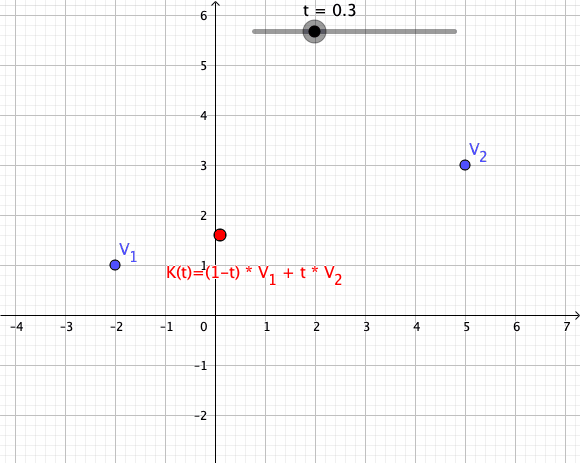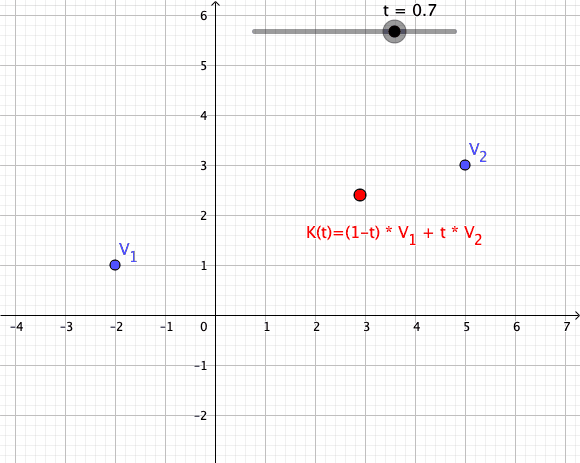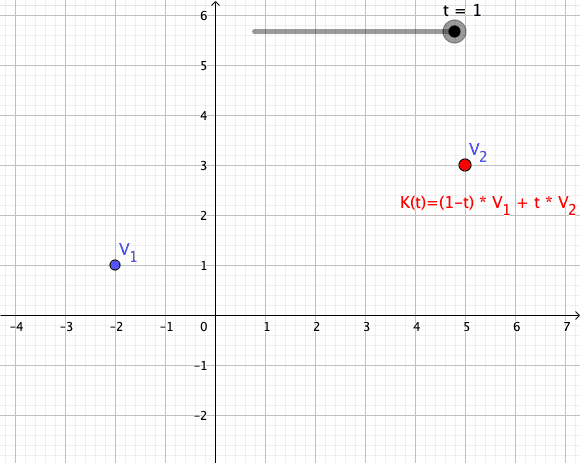
Convex Combination
In convex geometry and Vector space, vector algebra, a convex combination is a linear combination of point (geometry), points (which can be vector (geometric), vectors, scalar (mathematics), scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. Formal definition More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form : \alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex set, convex if it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Combination Illustration
Convex or convexity may refer to: Science and technology * Convex lens, in optics Mathematics * Convex set, containing the whole line segment that joins points ** Convex polygon, a polygon which encloses a convex set of points ** Convex polytope, a polytope with a convex set of points ** Convex metric space, a generalization of the convexity notion in abstract metric spaces * Convex function, when the line segment between any two points on the graph of the function lies above or on the graph * Convex conjugate, of a function * Convexity (algebraic geometry), a restrictive technical condition for algebraic varieties originally introduced to analyze Kontsevich Moduli space, moduli spaces Economics and finance * Convexity (finance), second derivatives in financial modeling generally * Convexity in economics * Bond convexity, a measure of the sensitivity of the duration of a bond to changes in interest rates * Convex preferences, an individual's ordering of various outcomes Other use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a set of points is convex if it contains every line segment between two points in the set. For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary (topology), boundary of a convex set in the plane is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval (mathematics), interval with the property that its epigraph (mathematics), epigraph (the set of points on or above the graph of a function, graph of the function) is a convex set. Convex minimization is a subfield of mathematical optimization, optimization that studies the problem of minimizing convex functions over convex sets. The branch of mathematics devoted to the study of properties of convex sets and convex f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example, * a 0-dimensional simplex is a point, * a 1-dimensional simplex is a line segment, * a 2-dimensional simplex is a triangle, * a 3-dimensional simplex is a tetrahedron, and * a 4-dimensional simplex is a 5-cell. Specifically, a -simplex is a -dimensional polytope that is the convex hull of its vertices. More formally, suppose the points u_0, \dots, u_k are affinely independent, which means that the vectors u_1 - u_0,\dots, u_k-u_0 are linearly independent. Then, the simplex determined by them is the set of points C = \left\. A regular simplex is a simplex that is also a regular polytope. A regular -simplex may be constructed from a regular -simplex by connecting a new vertex to all original vertices by the common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carathéodory's Theorem (convex Hull)
Carathéodory's theorem is a theorem in convex geometry. It states that if a point x lies in the convex hull \mathrm(P) of a set P\subset \R^d, then x lies in some ''d''-dimensional simplex with vertices in P. Equivalently, x can be written as the convex combination of d+1 or fewer points in P. Additionally, x can be written as the convex combination of at most d+1 ''extremal'' points in P, as non-extremal points can be removed from P without changing the membership of ''x'' in the convex hull. An equivalent theorem for conical combinations states that if a point x lies in the conical hull \mathrm(P) of a set P\subset \R^d, then x can be written as the conical combination of at most d points in P. Two other theorems of Helly and Radon are closely related to Carathéodory's theorem: the latter theorem can be used to prove the former theorems and vice versa. The result is named for Constantin Carathéodory, who proved the theorem in 1911 for the case when P is Compact space, co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Hull
In mathematics, the affine hull or affine span of a set ''S'' in Euclidean space R''n'' is the smallest affine set containing ''S'', or equivalently, the intersection of all affine sets containing ''S''. Here, an ''affine set'' may be defined as the translation of a vector subspace. The affine hull of ''S'' is what \operatorname S would be if the origin was moved to ''S''. The affine hull aff(''S'') of ''S'' is the set of all affine combinations of elements of ''S'', that is, :\operatorname (S)=\left\. Examples *The affine hull of the empty set is the empty set. *The affine hull of a singleton (a set made of one single element) is the singleton itself. *The affine hull of a set of two different points is the line through them. *The affine hull of a set of three points not on one line is the plane going through them. *The affine hull of a set of four points not in a plane in R''3'' is the entire space R''3''. Properties For any subsets S, T \subseteq X * \operatorname(\o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field (mathematics)
In mathematics, a field is a set (mathematics), set on which addition, subtraction, multiplication, and division (mathematics), division are defined and behave as the corresponding operations on rational number, rational and real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics. The best known fields are the field of rational numbers, the field of real numbers and the field of complex numbers. Many other fields, such as field of rational functions, fields of rational functions, algebraic function fields, algebraic number fields, and p-adic number, ''p''-adic fields are commonly used and studied in mathematics, particularly in number theory and algebraic geometry. Most cryptographic protocols rely on finite fields, i.e., fields with finitely many element (set), elements. The theory of fields proves that angle trisection and squaring the circle cannot be done with a compass and straighte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Combination
In mathematics, an affine combination of is a linear combination : \sum_^ = \alpha_ x_ + \alpha_ x_ + \cdots +\alpha_ x_, such that :\sum_^ =1. Here, can be elements ( vectors) of a vector space over a field , and the coefficients \alpha_ are elements of . The elements can also be points of a Euclidean space, and, more generally, of an affine space over a field . In this case the \alpha_ are elements of (or \mathbb R for a Euclidean space), and the affine combination is also a point. See for the definition in this case. This concept is fundamental in Euclidean geometry and affine geometry, because the set of all affine combinations of a set of points forms the smallest affine space containing the points, exactly as the linear combinations of a set of vectors form their linear span. The affine combinations commute with any affine transformation in the sense that : T\sum_^ = \sum_^. In particular, any affine combination of the fixed points of a given affine transform ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weight Function
A weight function is a mathematical device used when performing a sum, integral, or average to give some elements more "weight" or influence on the result than other elements in the same set. The result of this application of a weight function is a weighted sum or weighted average. Weight functions occur frequently in statistics and analysis, and are closely related to the concept of a measure. Weight functions can be employed in both discrete and continuous settings. They can be used to construct systems of calculus called "weighted calculus" and "meta-calculus".Jane Grossma''Meta-Calculus: Differential and Integral'' , 1981. Discrete weights General definition In the discrete setting, a weight function w \colon A \to \R^+ is a positive function defined on a discrete set A, which is typically finite or countable. The weight function w(a) := 1 corresponds to the ''unweighted'' situation in which all elements have equal weight. One can then apply this weight to various con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weighted Mean
The weighted arithmetic mean is similar to an ordinary arithmetic mean (the most common type of average), except that instead of each of the data points contributing equally to the final average, some data points contribute more than others. The notion of weighted mean plays a role in descriptive statistics and also occurs in a more general form in several other areas of mathematics. If all the weights are equal, then the weighted mean is the same as the arithmetic mean. While weighted means generally behave in a similar fashion to arithmetic means, they do have a few counterintuitive properties, as captured for instance in Simpson's paradox. Examples Basic example Given two school with 20 students, one with 30 test grades in each class as follows: :Morning class = :Afternoon class = The mean for the morning class is 80 and the mean of the afternoon class is 90. The unweighted mean of the two means is 85. However, this does not account for the difference in number of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Displacement (vector)
In geometry and mechanics, a displacement is a vector whose length is the shortest distance from the initial to the final position of a point P undergoing motion. It quantifies both the distance and direction of the net or total motion along a straight line from the initial position to the final position of the point trajectory. A displacement may be identified with the translation that maps the initial position to the final position. Displacement is the shift in location when an object in motion changes from one position to another. For motion over a given interval of time, the displacement divided by the length of the time interval defines the average velocity (a vector), whose magnitude is the average speed (a scalar quantity). Formulation A displacement may be formulated as a '' relative position'' (resulting from the motion), that is, as the final position of a point relative to its initial position . The corresponding displacement vector can be defined as the d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conical Combination
Given a finite number of vectors x_1, x_2, \dots, x_n in a real vector space, a conical combination, conical sum, or weighted sum''Convex Analysis and Minimization Algorithms'' by Jean-Baptiste Hiriart-Urruty, Claude Lemaréchal, 1993, pp. 101, 102/ref>''Mathematical Programming'', by Melvyn W. Jeter (1986) p. 68/ref> of these vectors is a vector of the form : \alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where \alpha_i are non-negative real numbers. The name derives from the fact that the set of all conical sum of vectors defines a cone (possibly in a lower-dimensional subspace). Conical hull The set of all conical combinations for a given set ''S'' is called the conical hull of ''S'' and denoted ''cone''(''S'') or ''coni''(''S''). That is, :\operatorname (S)=\left\. By taking ''k'' = 0, it follows the zero vector ( origin) belongs to all conical hulls (since the summation becomes an empty sum). The conical hull of a set ''S'' is a convex set. In fact, it is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Density Function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. More precisely, the PDF is used to specify the probability of the random variable falling ''within ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |