|
Conoidal
In geometry, a (general) conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the ''apex'' or ''vertex'' — and any point of some fixed space curve — the ''directrix'' — that does not contain the apex. Each of those lines is called a ''generatrix'' of the surface. Every conic surface is ruled and developable. In general, a conical surface consists of two congruent unbounded halves joined by the apex. Each half is called a nappe, and is the union of all the rays that start at the apex and pass through a point of some fixed space curve. (In some cases, however, the two nappes may intersect, or even coincide with the full surface.) Sometimes the term "conical surface" is used to mean just one nappe. If the directrix is a circle C, and the apex is located on the circle's ''axis'' (the line that contains the center of C and is perpendicular to its plane), one obtains the ''right circula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limiting Case (mathematics)
In mathematics, a limiting case of a mathematical object is a special case that arises when one or more components of the object take on their most extreme possible values. For example: * In statistics, the limiting case of the binomial distribution is the Poisson distribution. As the number of events tends to infinity in the binomial distribution, the random variable changes from the binomial to the Poisson distribution. *A circle is a limiting case of various other figures, including the Cartesian oval, the ellipse, the superellipse, and the Cassini oval. Each type of figure is a circle for certain values of the defining parameters, and the generic figure appears more like a circle as the limiting values are approached. *Archimedes calculated an approximate value of π by treating the circle as the limiting case of a regular polygon with 3 × 2''n'' sides, as ''n'' gets large. *In electricity and magnetism, the long wavelength limit is the limiting case when the wavelength is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surfaces
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. Surface or surfaces may also refer to: Mathematics *Surface (mathematics), a generalization of a plane which needs not be flat *Surface (differential geometry), a differentiable two-dimensional manifold *Surface (topology), a two-dimensional manifold * Algebraic surface, an algebraic variety of dimension two *Coordinate surfaces *Fractal surface, generated using a stochastic algorithm *Polyhedral surface * Surface area *Surface integral Arts and entertainment * Surface (band), an American R&B and pop trio ** ''Surface'' (Surface album), 1986 *Surfaces (band), American musical duo * ''Surface'' (Circle album), 1998 * "Surface" (Aero Chord song), 2014 * ''Surface'' (2005 TV series), an American science fiction show, 2005–2006 * ''Surface'' (2022 TV series), an American psychological thriller miniseries that began streaming in 2022 *'' The Surface'', an American film, 2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Solid Geometry
Euclidean (or, less commonly, Euclidian) is an adjective derived from the name of Euclid, an ancient Greek mathematician. It is the name of: Geometry *Euclidean space, the two-dimensional plane and three-dimensional space of Euclidean geometry as well as their higher dimensional generalizations *Euclidean geometry, the study of the properties of Euclidean spaces *Non-Euclidean geometry, systems of points, lines, and planes analogous to Euclidean geometry but without uniquely determined parallel lines *Euclidean distance, the distance between pairs of points in Euclidean spaces *Euclidean ball, the set of points within some fixed distance from a center point Number theory *Euclidean division, the division which produces a quotient and a remainder *Euclidean algorithm, a method for finding greatest common divisors *Extended Euclidean algorithm, a method for solving the Diophantine equation ''ax'' + ''by'' = ''d'' where ''d'' is the greatest common divisor of ''a'' and ''b'' *Euc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ruled Surface
In geometry, a surface is ruled (also called a scroll) if through every point of there is a straight line that lies on . Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space. A ruled surface can be described as the set of points swept by a moving straight line. For example, a cone is formed by keeping one point of a line fixed whilst moving another point along a circle. A surface is ''doubly ruled'' if through every one of its points there are two distinct lines that lie on the surface. The hyperbolic paraboloid and the hyperboloid of one sheet are doubly ruled surfaces. The plane is the only surface which contains at least three distinct lines through each of its points . The properties of being ruled or doubly ruled are preserved by projective maps, and therefore are concepts of projective geometry. In algebraic geometry, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadric
In mathematics, a quadric or quadric surface (quadric hypersurface in higher dimensions), is a generalization of conic sections (ellipses, parabolas, and hyperbolas). It is a hypersurface (of dimension ''D'') in a -dimensional space, and it is defined as the zero set of an irreducible polynomial of degree two in ''D'' + 1 variables; for example, in the case of conic sections. When the defining polynomial is not absolutely irreducible, the zero set is generally not considered a quadric, although it is often called a ''degenerate quadric'' or a ''reducible quadric''. In coordinates , the general quadric is thus defined by the algebraic equationSilvio LevQuadricsin "Geometry Formulas and Facts", excerpted from 30th Edition of ''CRC Standard Mathematical Tables and Formulas'', CRC Press, from The Geometry Center at University of Minnesota : \sum_^ x_i Q_ x_j + \sum_^ P_i x_i + R = 0 which may be compactly written in vector and matrix notation as: : x Q x^\mathrm + P x^\mathrm + ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Developable Surface
In mathematics, a developable surface (or torse: archaic) is a smooth surface with zero Gaussian curvature. That is, it is a surface that can be flattened onto a plane without distortion (i.e. it can be bent without stretching or compression). Conversely, it is a surface which can be made by transforming a plane (i.e. "folding", "bending", "rolling", "cutting" and/or "gluing"). In three dimensions all developable surfaces are ruled surfaces (but not vice versa). There are developable surfaces in four-dimensional space which are not ruled. The envelope of a single parameter family of planes is called a developable surface. Particulars The developable surfaces which can be realized in three-dimensional space include: *Cylinders and, more generally, the "generalized" cylinder; its cross-section may be any smooth curve *Cones and, more generally, conical surfaces; away from the apex * The oloid and the sphericon are members of a special family of solids that develop their e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
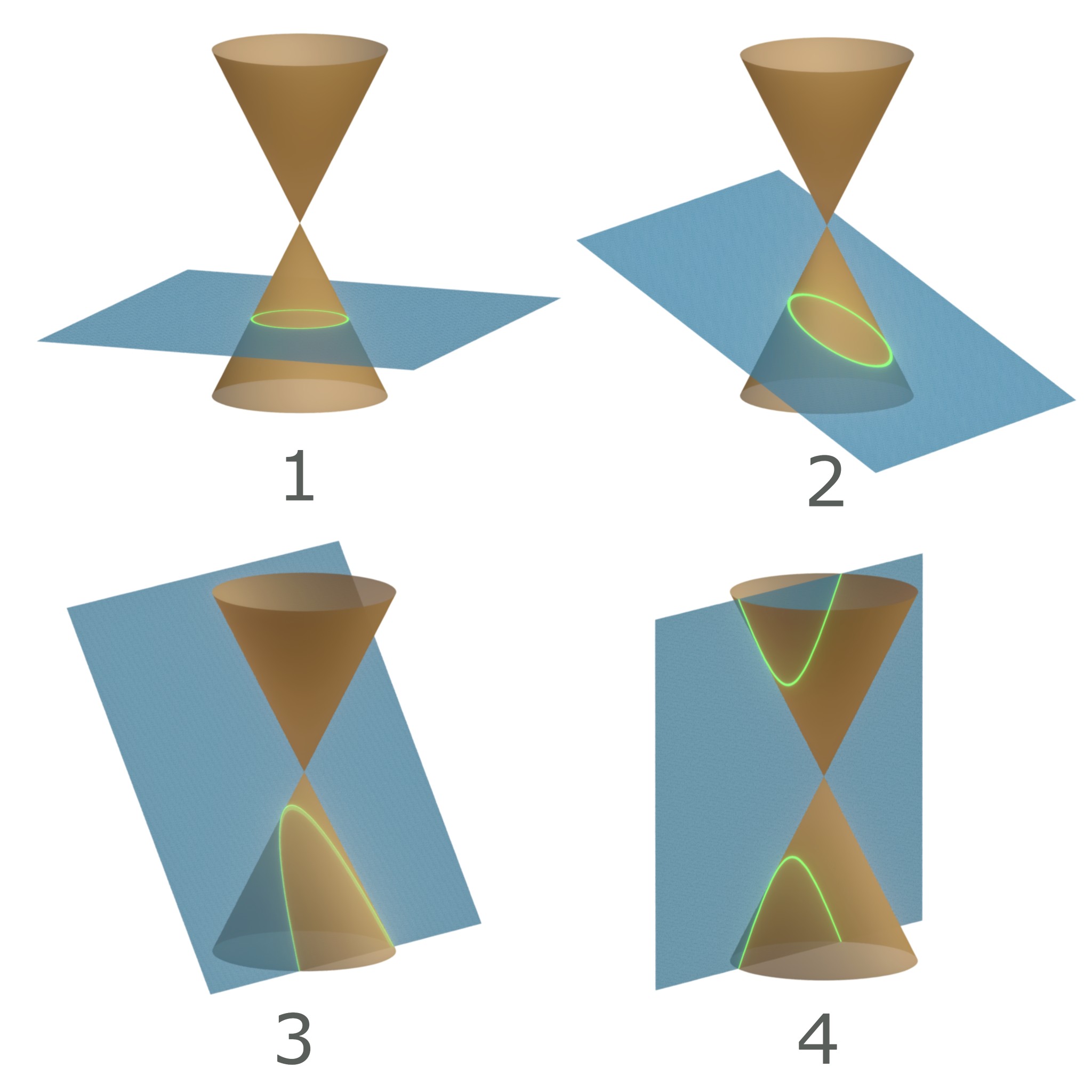
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a ''focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dot Product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more). Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. In mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Calculus
Vector calculus, or vector analysis, is concerned with differentiation and integration of vector fields, primarily in 3-dimensional Euclidean space \mathbb^3. The term "vector calculus" is sometimes used as a synonym for the broader subject of multivariable calculus, which spans vector calculus as well as partial differentiation and multiple integration. Vector calculus plays an important role in differential geometry and in the study of partial differential equations. It is used extensively in physics and engineering, especially in the description of electromagnetic fields, gravitational fields, and fluid flow. Vector calculus was developed from quaternion analysis by J. Willard Gibbs and Oliver Heaviside near the end of the 19th century, and most of the notation and terminology was established by Gibbs and Edwin Bidwell Wilson in their 1901 book, ''Vector Analysis''. In the conventional form using cross products, vector calculus does not generalize to higher dimensions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Implicit Equation
In mathematics, an implicit equation is a relation of the form R(x_1, \dots, x_n) = 0, where is a function of several variables (often a polynomial). For example, the implicit equation of the unit circle is x^2 + y^2 - 1 = 0. An implicit function is a function that is defined by an implicit equation, that relates one of the variables, considered as the value of the function, with the others considered as the arguments. For example, the equation x^2 + y^2 - 1 = 0 of the unit circle defines as an implicit function of if , and is restricted to nonnegative values. The implicit function theorem provides conditions under which some kinds of implicit equations define implicit functions, namely those that are obtained by equating to zero multivariable functions that are continuously differentiable. Examples Inverse functions A common type of implicit function is an inverse function. Not all functions have a unique inverse function. If is a function of that has a unique inverse, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametrization (geometry)
In mathematics, and more specifically in geometry, parametrization (or parameterization; also parameterisation, parametrisation) is the process of finding parametric equations of a curve, a surface, or, more generally, a manifold or a variety, defined by an implicit equation. The inverse process is called implicitization. "To parameterize" by itself means "to express in terms of parameters". Parametrization is a mathematical process consisting of expressing the state of a system, process or model as a function of some independent quantities called parameters. The state of the system is generally determined by a finite set of coordinates, and the parametrization thus consists of one function of several real variables for each coordinate. The number of parameters is the number of degrees of freedom of the system. For example, the position of a point that moves on a curve in three-dimensional space is determined by the time needed to reach the point when starting from a fixed orig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |