|
Compound Poisson Distribution
In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. The result can be either a continuous or a discrete distribution. Definition Suppose that :N\sim\operatorname(\lambda), i.e., ''N'' is a random variable whose distribution is a Poisson distribution with expected value λ, and that :X_1, X_2, X_3, \dots are identically distributed random variables that are mutually independent and also independent of ''N''. Then the probability distribution of the sum of N i.i.d. random variables :Y = \sum_^N X_n is a compound Poisson distribution. In the case ''N'' = 0, then this is a sum of 0 terms, so the value of ''Y'' is 0. Hence the conditional distribution of ''Y'' given that ''N'' = 0 is a degenerate distribution. The compound Poisson distribution is obtained by marginalising the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment (mathematics)
In mathematics, the moments of a function are certain quantitative measures related to the shape of the function's graph. If the function represents mass density, then the zeroth moment is the total mass, the first moment (normalized by total mass) is the center of mass, and the second moment is the moment of inertia. If the function is a probability distribution, then the first moment is the expected value, the second central moment is the variance, the third standardized moment is the skewness, and the fourth standardized moment is the kurtosis. For a distribution of mass or probability on a bounded interval, the collection of all the moments (of all orders, from to ) uniquely determines the distribution ( Hausdorff moment problem). The same is not true on unbounded intervals ( Hamburger moment problem). In the mid-nineteenth century, Pafnuty Chebyshev became the first person to think systematically in terms of the moments of random variables. Significance of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Actuarial Science
Actuarial science is the discipline that applies mathematics, mathematical and statistics, statistical methods to Risk assessment, assess risk in insurance, pension, finance, investment and other industries and professions. Actuary, Actuaries are professionals trained in this discipline. In many countries, actuaries must demonstrate their competence by passing a series of rigorous professional examinations focused in fields such as probability and predictive analysis. Actuarial science includes a number of interrelated subjects, including mathematics, probability theory, statistics, finance, economics, financial accounting and computer science. Historically, actuarial science used deterministic models in the construction of tables and premiums. The science has gone through revolutionary changes since the 1980s due to the proliferation of high speed computers and the union of stochastic actuarial models with modern financial theory. Many universities have undergraduate and gradu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of The Operational Research Society
The ''Journal of the Operational Research Society'' is a monthly peer-reviewed academic journal covering operations research. It is an official journal of the Operational Research Society and publishes full length case-oriented papers, full length theoretical papers, technical notes, discussions (viewpoints) and book reviews. It was established in 1950 as the ''Operational Research Quarterly'' (from 1953 to 1969 under the title ''OR''). It was published four times a year until 1978 when it became a monthly publication and the name was changed to ''Journal of the Operational Research Society''. In 2024, the journal celebrated its 75th anniversary. Abstracting and indexing The journal is abstracted and indexed in: *Current Contents/Engineering, Computing & Technology *Current Contents/Social & Behavioural Sciences * Ei Compendex *Inspec *Science Citation Index Expanded *Social Sciences Citation Index *Scopus *Zentralblatt MATH According to the ''Journal Citation Reports'', the journa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bulk Queue
In queueing theory, a discipline within the mathematical theory of probability, a bulk queue (sometimes batch queue) is a general queueing model where jobs arrive in and/or are served in groups of random size. Batch arrivals have been used to describe large deliveries and batch services to model a hospital out-patient department holding a clinic once a week, a transport link with fixed capacity and an elevator. Networks of such queues are known to have a product form stationary distribution under certain conditions. Under heavy traffic conditions a bulk queue is known to behave like a reflected Brownian motion. Kendall's notation In Kendall's notation for single queueing nodes, the random variable denoting bulk arrivals or service is denoted with a superscript, for example M''X''/M''Y''/1 denotes an M/M/1 queue where the arrivals are in batches determined by the random variable ''X'' and the services in bulk determined by the random variable ''Y''. In a similar way, the GI/G/1 qu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Divisibility (probability)
Infinite may refer to: Mathematics * Infinite set, a set that is not a finite set * Infinity, an abstract concept describing something without any limit Music Performers * Infinite (group), a South Korean boy band * Infinite (rapper), Canadian rapper Albums * ''Infinite'' (Deep Purple album), 2017 * ''Infinite'' (Eminem album) or the title song (see below), 1996 * ''Infinite'' (Sam Concepcion album), 2013 * ''Infinite'' (Stratovarius album), 2000 * ''The Infinite'' (album), by Dave Douglas, 2002 *''Infinite'', by Kazumi Watanabe, 1971 *''Infinite'', an EP by Haywyre, 2012 Songs * "Infinite" (Beni Arashiro song), 2004 * "Infinite" (Eminem song), 1996 * "Infinite" (Notaker song), 2016 *"Infinite", by Forbidden from '' Twisted into Form'', 1990 Other uses * ''Infinite'' (film), a 2021 science fiction film *" The Infinites", a 1953 science fiction short story by Philip K. Dick *The Infinites, a fictional group of cosmic beings in the '' Avengers Infinity'' comic book series *I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Luria–Delbrück Experiment
The Luria–Delbrück experiment (1943) (also called the Fluctuation Test) demonstrated that in bacteria, genetic mutations arise in the absence of selective pressure rather than being a response to it. Thus, it concluded Darwin's theory of natural selection acting on random mutations applies to bacteria as well as to more complex organisms. Max Delbrück and Salvador Luria won the 1969 Nobel Prize in Physiology or Medicine in part for this work. Simple model Suppose a single bacterium is introduced to a growth medium with rich nutrients, and allowed to grow for N\times of its doubling time, we would obtain 2^N offsprings. Then, we introduce a ''challenge'' by bacteriophages. This would kill off most bacteria, but leave some alive. We can then smear the growth medium over a new growth medium, and count the number of colonies as the number of survivors. In the Lamarckian scenario, each bacterium faces the challenge alone. Most would perish, but a few would survive the ordeal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
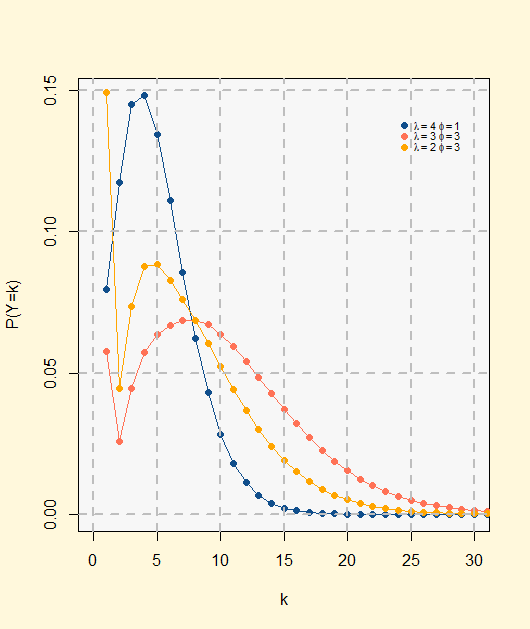
Neyman Type A Distribution
In statistics and probability, the Neyman Type A distribution is a discrete probability distribution from the family of Compound Poisson distribution. First of all, to easily understand this distribution we will demonstrate it with the following example explained in Univariate Discret Distributions; we have a statistical model of the distribution of larvae in a unit area of field (in a unit of habitat) by assuming that the variation in the number of clusters of eggs per unit area (per unit of habitat) could be represented by a Poisson distribution with parameter \lambda , while the number of larvae developing per cluster of eggs are assumed to have independent Poisson distribution all with the same parameter \phi . If we want to know how many larvae there are, we define a random variable ''Y'' as the sum of the number of larvae hatched in each group (given ''j'' groups). Therefore, ''Y'' = ''X''1 + ''X''2 + ... ''X'' j, where ''X''1,...,''X''j are independent Poisson variables w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
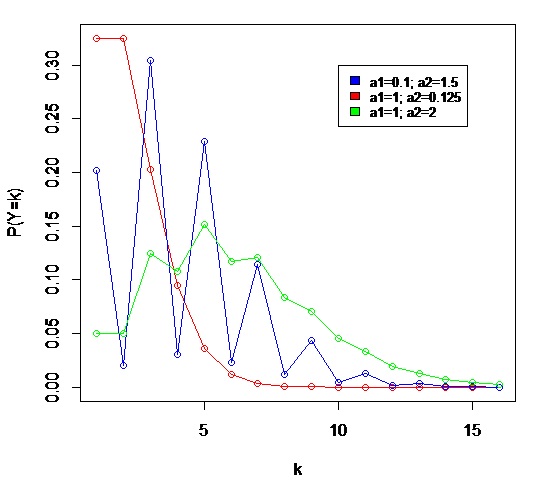
Geometric Poisson Distribution
In probability theory and statistics, the geometric Poisson distribution (also called the Pólya–Aeppli distribution) is used for describing objects that come in clusters, where the number of clusters follows a Poisson distribution and the number of objects within a cluster follows a geometric distribution. It is a particular case of the compound Poisson distribution. The probability mass function of a random variable ''N'' distributed according to the geometric Poisson distribution \mathcal(\lambda,\theta) is given by : f_N(n) = \mathrm(N=n)= \begin \sum_^n e^\frac(1-\theta)^\theta^k\binom, & n>0 \\ e^, & n=0 \end where ''λ'' is the parameter of the underlying Poisson distribution and θ is the parameter of the geometric distribution. The distribution was described by George Pólya in 1930. Pólya credited his student Alfred Aeppli's 1924 dissertation as the original source. It was called the geometric Poisson distribution by Sherbrooke in 1968, who gave probability tables w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negative Binomial Distribution
In probability theory and statistics, the negative binomial distribution, also called a Pascal distribution, is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified/constant/fixed number of successes r occur. For example, we can define rolling a 6 on some dice as a success, and rolling any other number as a failure, and ask how many failure rolls will occur before we see the third success (r=3). In such a case, the probability distribution of the number of failures that appear will be a negative binomial distribution. An alternative formulation is to model the number of total trials (instead of the number of failures). In fact, for a specified (non-random) number of successes , the number of failures is random because the number of total trials is random. For example, we could use the negative binomial distribution to model the number of days (random) a certain machin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Distribution
In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions: * The probability distribution of the number X of Bernoulli trials needed to get one success, supported on \mathbb = \; * The probability distribution of the number Y=X-1 of failures before the first success, supported on \mathbb_0 = \ . These two different geometric distributions should not be confused with each other. Often, the name ''shifted'' geometric distribution is adopted for the former one (distribution of X); however, to avoid ambiguity, it is considered wise to indicate which is intended, by mentioning the support explicitly. The geometric distribution gives the probability that the first occurrence of success requires k independent trials, each with success probability p. If the probability of success on each trial is p, then the probability that the k-th trial is the first success is :\Pr(X = k) = (1-p)^p for k=1,2,3,4,\dots The above form of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermite Distribution
In probability theory and statistics, the Hermite distribution, named after Charles Hermite, is a discrete probability distribution used to model ''count data'' with more than one parameter. This distribution is flexible in terms of its ability to allow a moderate over-dispersion in the data. The authors C. D. Kemp and A. W. Kemp have called it "Hermite distribution" from the fact its probability function and the moment generating function can be expressed in terms of the coefficients of (modified) Hermite polynomials. History The distribution first appeared in the paper ''Applications of Mathematics to Medical Problems'', by Anderson Gray McKendrick in 1926. In this work the author explains several mathematical methods that can be applied to medical research. In one of this methods he considered the bivariate Poisson distribution and showed that the distribution of the sum of two correlated Poisson variables follow a distribution that later would be known as Hermite distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |