|
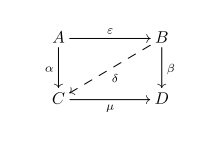
Coequaliser
In category theory, a coequalizer (or coequaliser) is a generalization of a quotient set, quotient by an equivalence relation to objects in an arbitrary category (mathematics), category. It is the categorical construction dual (category theory), dual to the equaliser (mathematics), equalizer. Definition A coequalizer is a colimit of the diagram consisting of two objects ''X'' and ''Y'' and two parallel morphisms ''f'', ''g'' : ''X'' → ''Y''. More explicitly, a coequalizer can be defined as an object ''Q'' together with a morphism ''q'' : ''Y'' → ''Q'' such that ''q'' ∘ ''f'' = ''q'' ∘ ''g''. Moreover, the pair (''Q'', ''q'') must be universal property, universal in the sense that given any other such pair (''Q''′, ''q''′) there exists a unique morphism ''u'' : ''Q'' → ''Q''′ such that ''u'' ∘ ''q'' = ''q''′. This information can be captured by the following commutative diagram: As with all universal constructions, a coequalizer, if it ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Theory
Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Nowadays, category theory is used in almost all areas of mathematics, and in some areas of computer science. In particular, many constructions of new mathematical objects from previous ones, that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient spaces, direct products, completion, and duality. A category is formed by two sorts of objects: the objects of the category, and the morphisms, which relate two objects called the ''source'' and the ''target'' of the morphism. One often says that a morphism is an ''arrow'' that ''maps'' its source to its target. Morphisms can be ''composed'' if the target of the first morphism equals the source of the second one, and morphism compos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prentice Hall International Series In Computer Science
Prentice Hall International Series in Computer Science was a series of books on computer science published by Prentice Hall. The series' founding editor was Tony Hoare. Richard Bird subsequently took over editing the series. Many of the books in the series have been in the area of formal methods in particular. Selected books The following books were published in the series: * R. S. Bird, ''Introduction to Functional Programming using Haskell'', 2nd edition, 1998. . * R. S. Bird and O. de Moor, ''Algebra of Programming'', 1996. . (100th volume in the series.) * O.-J. Dahl, ''Verifiable Programming'', 1992. . * D. M. Gabbay, ''Elementary Logics: A Procedural Perspective'', 1998. . * I. J. Hayes (ed.), ''Specification Cases Studies'', 2nd edition, 1993. . * M. G. Hinchey and J. P. Bowen (eds.), ''Applications of Formal Methods'', 1996. . * C. A. R. Hoare, ''Communicating Sequential Processes'', 1985. hardback or paperback. * C. A. R. Hoare and M. J. C. Gordon, ''Mechanized Re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epimorphism
In category theory, an epimorphism (also called an epic morphism or, colloquially, an epi) is a morphism ''f'' : ''X'' → ''Y'' that is right-cancellative in the sense that, for all objects ''Z'' and all morphisms , : g_1 \circ f = g_2 \circ f \implies g_1 = g_2. Epimorphisms are categorical analogues of onto or surjective functions (and in the category of sets the concept corresponds exactly to the surjective functions), but they may not exactly coincide in all contexts; for example, the inclusion \mathbb\to\mathbb is a ring epimorphism. The dual of an epimorphism is a monomorphism (i.e. an epimorphism in a category ''C'' is a monomorphism in the dual category ''C''op). Many authors in abstract algebra and universal algebra define an epimorphism simply as an ''onto'' or surjective homomorphism. Every epimorphism in this algebraic sense is an epimorphism in the sense of category theory, but the converse is not true in all categories. In this article, the term "epimorphism" w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country"). Numbers used for counting are called ''Cardinal number, cardinal numbers'', and numbers used for ordering are called ''Ordinal number, ordinal numbers''. Natural numbers are sometimes used as labels, known as ''nominal numbers'', having none of the properties of numbers in a mathematical sense (e.g. sports Number (sports), jersey numbers). Some definitions, including the standard ISO/IEC 80000, ISO 80000-2, begin the natural numbers with , corresponding to the non-negative integers , whereas others start with , corresponding to the positive integers Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers). The natural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monoid
In abstract algebra, a branch of mathematics, a monoid is a set equipped with an associative binary operation and an identity element. For example, the nonnegative integers with addition form a monoid, the identity element being 0. Monoids are semigroups with identity. Such algebraic structures occur in several branches of mathematics. The functions from a set into itself form a monoid with respect to function composition. More generally, in category theory, the morphisms of an object to itself form a monoid, and, conversely, a monoid may be viewed as a category with a single object. In computer science and computer programming, the set of strings built from a given set of characters is a free monoid. Transition monoids and syntactic monoids are used in describing finite-state machines. Trace monoids and history monoids provide a foundation for process calculi and concurrent computing. In theoretical computer science, the study of monoids is fundamental for automata ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |