|
Boundedly Generated Group
In mathematics, a group is called boundedly generated if it can be expressed as a finite product of cyclic subgroups. The property of bounded generation is also closely related with the congruence subgroup problem (see ). Definitions A group ''G'' is called ''boundedly generated'' if there exists a finite subset ''S'' of ''G'' and a positive integer ''m'' such that every element ''g'' of ''G'' can be represented as a product of at most ''m'' powers of the elements of ''S'': : g = s_1^ \cdots s_m^, where s_i \in S and k_i are integers. The finite set ''S'' generates ''G'', so a boundedly generated group is finitely generated. An equivalent definition can be given in terms of cyclic subgroups. A group ''G'' is called ''boundedly generated'' if there is a finite family ''C''1, …, ''C''''M'' of not necessarily distinct cyclic subgroups such that ''G'' = ''C''1…''C''''M'' as a set. Properties * Bounded generation is unaffected by passing to a subgroup of finite i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic K-theory
Algebraic ''K''-theory is a subject area in mathematics with connections to geometry, topology, ring theory, and number theory. Geometric, algebraic, and arithmetic objects are assigned objects called ''K''-groups. These are groups in the sense of abstract algebra. They contain detailed information about the original object but are notoriously difficult to compute; for example, an important outstanding problem is to compute the ''K''-groups of the integers. ''K''-theory was discovered in the late 1950s by Alexander Grothendieck in his study of intersection theory on algebraic varieties. In the modern language, Grothendieck defined only ''K''0, the zeroth ''K''-group, but even this single group has plenty of applications, such as the Grothendieck–Riemann–Roch theorem. Intersection theory is still a motivating force in the development of (higher) algebraic ''K''-theory through its links with motivic cohomology and specifically Chow groups. The subject also includes classical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stirling's Approximation
In mathematics, Stirling's approximation (or Stirling's formula) is an approximation for factorials. It is a good approximation, leading to accurate results even for small values of n. It is named after James Stirling, though a related but less precise result was first stated by Abraham de Moivre. One way of stating the approximation involves the logarithm of the factorial: \ln(n!) = n\ln n - n +O(\ln n), where the big O notation means that, for all sufficiently large values of n, the difference between \ln(n!) and n\ln n-n will be at most proportional to the logarithm. In computer science applications such as the worst-case lower bound for comparison sorting, it is convenient to use instead the binary logarithm, giving the equivalent form \log_2 (n!) = n\log_2 n - n\log_2 e +O(\log_2 n). The error term in either base can be expressed more precisely as \tfrac12\log(2\pi n)+O(\tfrac1n), corresponding to an approximate formula for the factorial itself, n! \sim \sqrt\left(\frac\righ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
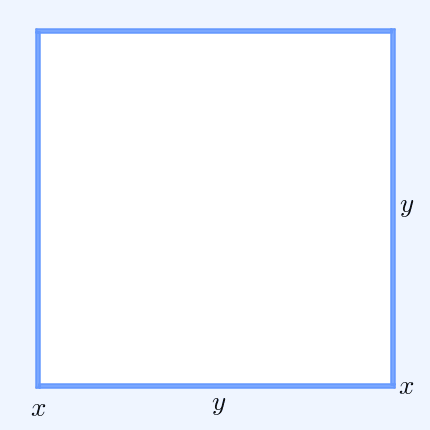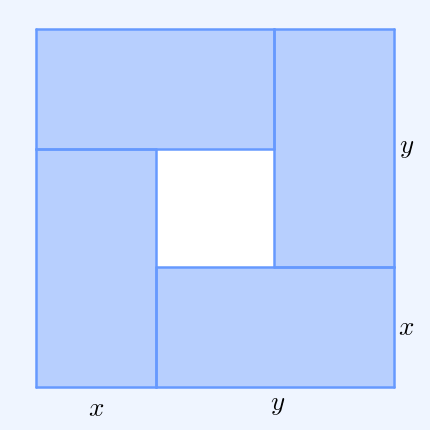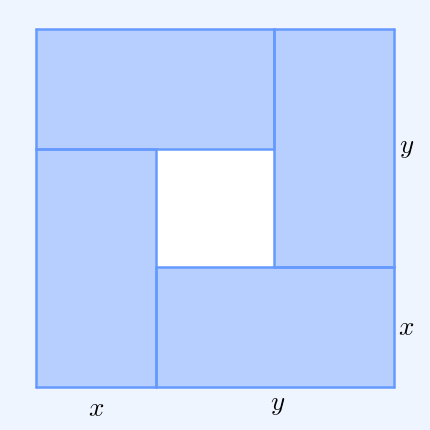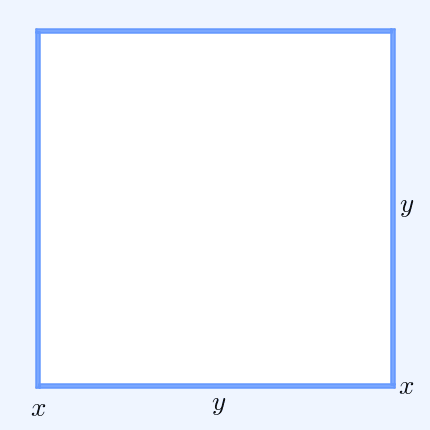
Inequality Of Arithmetic And Geometric Means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if every number in the list is the same (in which case they are both that number). The simplest non-trivial case – i.e., with more than one variable – for two non-negative numbers and , is the statement that :\frac2 \ge \sqrt with equality if and only if . This case can be seen from the fact that the square of a real number is always non-negative (greater than or equal to zero) and from the elementary case of the binomial formula: :\begin 0 & \le (x-y)^2 \\ & = x^2-2xy+y^2 \\ & = x^2+2xy+y^2 - 4xy \\ & = (x+y)^2 - 4xy. \end Hence , with equality precisely when , i.e. . The AM–GM inequality then follows from taking the positive square root of both sides and then dividing both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutation
In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements. The word "permutation" also refers to the act or process of changing the linear order of an ordered set. Permutations differ from combinations, which are selections of some members of a set regardless of order. For example, written as tuples, there are six permutations of the set , namely (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), and (3, 2, 1). These are all the possible orderings of this three-element set. Anagrams of words whose letters are different are also permutations: the letters are already ordered in the original word, and the anagram is a reordering of the letters. The study of permutations of finite sets is an important topic in the fields of combinatorics and group theory. Permutations are used in almost every branch of mathematics, and in many other fields of scie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycle Decomposition (group Theory)
In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements. The word "permutation" also refers to the act or process of changing the linear order of an ordered set. Permutations differ from combinations, which are selections of some members of a set regardless of order. For example, written as tuples, there are six permutations of the set , namely (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), and (3, 2, 1). These are all the possible orderings of this three-element set. Anagrams of words whose letters are different are also permutations: the letters are already ordered in the original word, and the anagram is a reordering of the letters. The study of permutations of finite sets is an important topic in the fields of combinatorics and group theory. Permutations are used in almost every branch of mathematics, and in many other fields of scien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edmund Landau
Edmund Georg Hermann Landau (14 February 1877 – 19 February 1938) was a German mathematician who worked in the fields of number theory and complex analysis. Biography Edmund Landau was born to a Jewish family in Berlin. His father was Leopold Landau, a gynecologist and his mother was Johanna Jacoby. Landau studied mathematics at the University of Berlin, receiving his doctorate in 1899 and his habilitation (the post-doctoral qualification required to teach in German universities) in 1901. His doctoral thesis was 14 pages long. In 1895, his paper on scoring chess tournaments is the earliest use of eigenvector centrality. Landau taught at the University of Berlin from 1899 to 1909, after which he held a chair at the University of Göttingen. He married Marianne Ehrlich, the daughter of the Nobel Prize-winning biologist Paul Ehrlich, in 1905. At the 1912 International Congress of Mathematicians Landau listed four problems in number theory about primes that he said were parti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Number
The number , also known as Euler's number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of a logarithm, base of the natural logarithms. It is the Limit of a sequence, limit of as approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite Series (mathematics), series e = \sum\limits_^ \frac = 1 + \frac + \frac + \frac + \cdots. It is also the unique positive number such that the graph of the function has a slope of 1 at . The (natural) exponential function is the unique function that equals its own derivative and satisfies the equation ; hence one can also define as . The natural logarithm, or logarithm to base , is the inverse function to the natural exponential function. The natural logarithm of a number can be defined directly as the integral, area under the curve between and , in which case is the value of for which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group \mathrm_n defined over a finite set of n symbols consists of the permutations that can be performed on the n symbols. Since there are n! (n factorial) such permutation operations, the order (number of elements) of the symmetric group \mathrm_n is n!. Although symmetric groups can be defined on infinite sets, this article focuses on the finite symmetric groups: their applications, their elements, their conjugacy classes, a finite presentation, their subgroups, their automorphism groups, and their representation theory. For the remainder of this article, "symmetric group" will mean a symmetric group on a finite set. The symmetric group is important to diverse areas of mathematics such as Galois theory, invariant theory, the representatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automata Theory
Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science. The word ''automata'' comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton (automata in plural) is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite-State Machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states (represented in the figure by circles) and transitions (represented by arrows). As the automaton sees a symbol of input, it makes a transition (or jump) to another state, according to its transition function, which takes the previous state and current input symbol as its arguments. Automata theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Burnside Problem
The Burnside problem asks whether a finitely generated group in which every element has finite order must necessarily be a finite group. It was posed by William Burnside in 1902, making it one of the oldest questions in group theory and was influential in the development of combinatorial group theory. It is known to have a negative answer in general, as Evgeny Golod and Igor Shafarevich provided a counter-example in 1964. The problem has many refinements and variants (see bounded and restricted below) that differ in the additional conditions imposed on the orders of the group elements, some of which are still open questions. Brief history Initial work pointed towards the affirmative answer. For example, if a group ''G'' is finitely generated and the order of each element of ''G'' is a divisor of 4, then ''G'' is finite. Moreover, A. I. Kostrikin was able to prove in 1958 that among the finite groups with a given number of generators and a given prime exponent, there exists a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golod–Shafarevich Theorem
In mathematics, the Golod–Shafarevich theorem was proved in 1964 by Evgeny Golod and Igor Shafarevich. It is a result in non-commutative homological algebra which solves the class field tower problem, by showing that class field towers can be infinite. The inequality Let ''A'' = ''K''⟨''x''1, ..., ''x''''n''⟩ be the free algebra over a field ''K'' in ''n'' = ''d'' + 1 non-commuting variables ''x''''i''. Let ''J'' be the 2-sided ideal of ''A'' generated by homogeneous elements ''f''''j'' of ''A'' of degree ''d''''j'' with :2 ≤ ''d''1 ≤ ''d''2 ≤ ... where ''d''''j'' tends to infinity. Let ''r''''i'' be the number of ''d''''j'' equal to ''i''. Let ''B''=''A''/''J'', a graded algebra. Let ''b''''j'' = dim ''B''''j''. The ''fundamental inequality'' of Golod and Shafarevich states that :: b_j\ge nb_ -\sum_^ b_ r_i. As a consequence: * ''B'' is infinite-dimensional if ''r''''i'' ≤ ''d''2/4 for all ''i'' Applications This result has important applicatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |