|
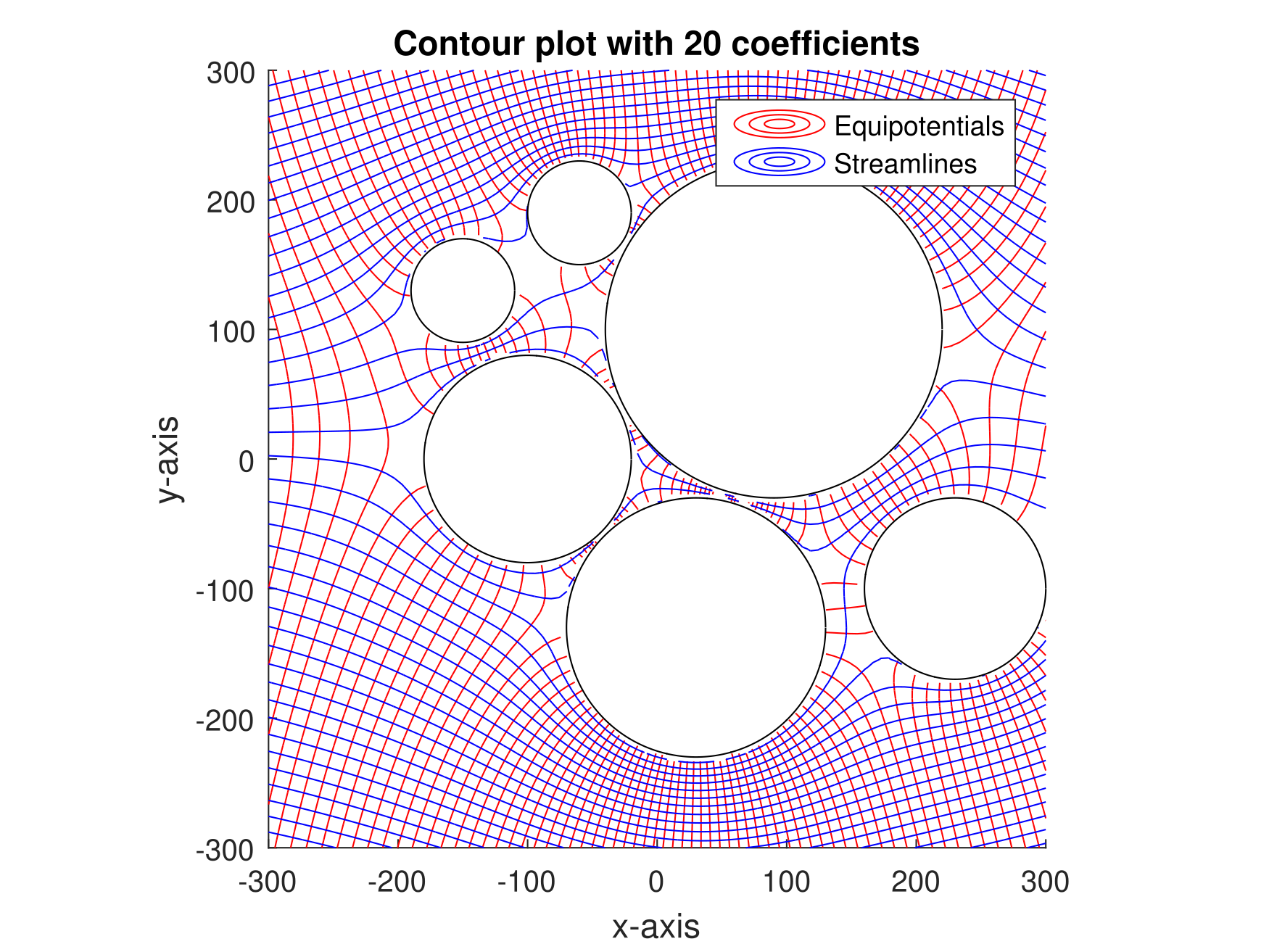
Boundary Element
The boundary element method (BEM) is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations (i.e. in ''boundary integral'' form), including fluid mechanics, acoustics, electromagnetics (where the technique is known as method of moments or abbreviated as MoM), fracture mechanics, and contact mechanics. Mathematical basis The integral equation may be regarded as an exact solution of the governing partial differential equation. The boundary element method attempts to use the given boundary conditions to fit boundary values into the integral equation, rather than values throughout the space defined by a partial differential equation. Once this is done, in the post-processing stage, the integral equation can then be used again to calculate numerically the solution directly at any desired point in the interior of the solution domain. BEM is applicable to problems for which Green's functions can be calculated. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives. The function is often thought of as an "unknown" that solves the equation, similar to how is thought of as an unknown number solving, e.g., an algebraic equation like . However, it is usually impossible to write down explicit formulae for solutions of partial differential equations. There is correspondingly a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity and stability. Among the many open questions are the existence an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gauss Quadrature
In numerical analysis, an -point Gaussian quadrature rule, named after Carl Friedrich Gauss, is a quadrature rule constructed to yield an exact result for polynomials of degree or less by a suitable choice of the nodes and weights for . The modern formulation using orthogonal polynomials was developed by Carl Gustav Jacobi in 1826. The most common domain of integration for such a rule is taken as , so the rule is stated as \int_^1 f(x)\,dx \approx \sum_^n w_i f(x_i), which is exact for polynomials of degree or less. This exact rule is known as the Gauss–Legendre quadrature rule. The quadrature rule will only be an accurate approximation to the integral above if is well-approximated by a polynomial of degree or less on . The Gauss– Legendre quadrature rule is not typically used for integrable functions with endpoint singularities. Instead, if the integrand can be written as f(x) = \left(1 - x\right)^\alpha \left(1 + x\right)^\beta g(x),\quad \alpha,\beta > -1, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computational Electromagnetics
Computational electromagnetics (CEM), computational electrodynamics or electromagnetic modeling is the process of modeling the interaction of electromagnetic fields with physical objects and the environment using computers. It typically involves using computer programs to compute approximate solutions to Maxwell's equations to calculate antenna performance, electromagnetic compatibility, radar cross section and electromagnetic wave propagation when not in free space. A large subfield is antenna modeling computer programs, which calculate the radiation pattern and electrical properties of radio antennas, and are widely used to design antennas for specific applications. Background Several real-world electromagnetic problems like electromagnetic scattering, electromagnetic radiation, modeling of waveguides etc., are not analytically calculable, for the multitude of irregular geometries found in actual devices. Computational numerical techniques can overcome the inability to de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Analytic Element Method
The analytic element method (AEM) is a numerical method used for the solution of partial differential equations. It was initially developed by O.D.L. Strack at the University of Minnesota. It is similar in nature to the boundary element method (BEM), as it does not rely upon the discretization of volumes or areas in the modeled system; only internal and external boundaries are discretized. One of the primary distinctions between AEM and BEMs is that the boundary integrals are calculated analytically. Although originally developed to model groundwater flow, AEM has subsequently been applied to other fields of study including studies of heat flow and conduction, periodic waves, and deformation by force. Mathematical basis The basic premise of the analytic element method is that, for linear differential equations, elementary solutions may be superimposed to obtain more complex solutions. A suite of 2D and 3D analytic solutions ("elements") are available for different governing equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hierarchical Matrix
In numerical mathematics, hierarchical matrices (H-matrices) are used as data-sparse approximations of non-sparse matrices. While a sparse matrix of dimension n can be represented efficiently in O(n) units of storage by storing only its non-zero entries, a non-sparse matrix would require O(n^2) units of storage, and using this type of matrices for large problems would therefore be prohibitively expensive in terms of storage and computing time. Hierarchical matrices provide an approximation requiring only O(n k\,\log(n)) units of storage, where k is a parameter controlling the accuracy of the approximation. In typical applications, e.g., when discretizing integral equations, preconditioning the resulting systems of linear equations, or solving elliptic partial differential equations, a rank proportional to \log(1/\epsilon)^\gamma with a small constant \gamma is sufficient to ensure an accuracy of \epsilon. Compared to many other data-sparse representations of non-sparse matrices, hie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Slosh Dynamics
In fluid dynamics, slosh refers to the movement of liquid inside another object (which is, typically, also undergoing motion). Strictly speaking, the liquid must have a free surface to constitute a slosh dynamics problem, where the dynamics of the liquid can interact with the container to alter the system dynamics significantly. Important examples include propellant slosh in spacecraft tanks and rockets (especially upper stages), and the free surface effect (cargo slosh) in ships and trucks transporting liquids (for example oil and gasoline). However, it has become common to refer to liquid motion in a completely filled tank, i.e. without a free surface, as "fuel slosh". Such motion is characterized by " inertial waves" and can be an important effect in spinning spacecraft dynamics. Extensive mathematical and empirical relationships have been derived to describe liquid slosh. These types of analyses are typically undertaken using computational fluid dynamics and finite element m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Natural Frequencies
The fundamental frequency, often referred to simply as the ''fundamental'' (abbreviated as 0 or 1 ), is defined as the lowest frequency of a periodic waveform. In music, the fundamental is the musical pitch of a note that is perceived as the lowest partial present. In terms of a superposition of sinusoids, the fundamental frequency is the lowest frequency sinusoidal in the sum of harmonically related frequencies, or the frequency of the difference between adjacent frequencies. In some contexts, the fundamental is usually abbreviated as 0, indicating the lowest frequency counting from zero. In other contexts, it is more common to abbreviate it as 1, the first harmonic. (The second harmonic is then 2 = 2⋅1, etc.) According to Benward and Saker's ''Music: In Theory and Practice'': Explanation All sinusoidal and many non-sinusoidal waveforms repeat exactly over time – they are periodic. The period of a waveform is the smallest positive value T for which the following is tru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Finite Volume Method
The finite volume method (FVM) is a method for representing and evaluating partial differential equations in the form of algebraic equations. In the finite volume method, volume integrals in a partial differential equation that contain a divergence term are converted to surface integrals, using the divergence theorem. These terms are then evaluated as fluxes at the surfaces of each finite volume. Because the flux entering a given volume is identical to that leaving the adjacent volume, these methods are conservative. Another advantage of the finite volume method is that it is easily formulated to allow for unstructured meshes. The method is used in many computational fluid dynamics packages. "Finite volume" refers to the small volume surrounding each node point on a mesh. Finite volume methods can be compared and contrasted with the finite difference methods, which approximate derivatives using nodal values, or finite element methods, which create local approximations of a so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Finite Difference Method
In numerical analysis, finite-difference methods (FDM) are a class of numerical techniques for solving differential equations by approximating Derivative, derivatives with Finite difference approximation, finite differences. Both the spatial domain and time domain (if applicable) are Discretization, discretized, or broken into a finite number of intervals, and the values of the solution at the end points of the intervals are approximated by solving algebraic equations containing finite differences and values from nearby points. Finite difference methods convert ordinary differential equations (ODE) or partial differential equations (PDE), which may be Nonlinear partial differential equation, nonlinear, into a system of linear equations that can be solved by matrix algebra techniques. Modern computers can perform these linear algebra computations efficiently, and this, along with their relative ease of implementation, has led to the widespread use of FDM in modern numerical analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Finite Element Method
Finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. Computers are usually used to perform the calculations required. With high-speed supercomputers, better solutions can be achieved and are often required to solve the largest and most complex problems. FEM is a general numerical method for solving partial differential equations in two- or three-space variables (i.e., some boundary value problems). There are also studies about using FEM to solve high-dimensional problems. To solve a problem, FEM subdivides a large system into smaller, simpler parts called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a mesh of the object: the numer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mesh
Medical Subject Headings (MeSH) is a comprehensive controlled vocabulary for the purpose of indexing journal articles and books in the life sciences. It serves as a thesaurus of index terms that facilitates searching. Created and updated by the United States National Library of Medicine (NLM), it is used by the MEDLINE/PubMed article database and by NLM's catalog of book holdings. MeSH is also used by ClinicalTrials.gov registry to classify which diseases are studied by trials registered in ClinicalTrials. MeSH was introduced in the 1960s, with the NLM's own index catalogue and the subject headings of the Quarterly Cumulative Index Medicus (1940 edition) as precursors. The yearly printed version of MeSH was discontinued in 2007; MeSH is now available only online. It can be browsed and downloaded free of charge through PubMed. Originally in English, MeSH has been translated into numerous other languages and allows retrieval of documents from different origins. Structure MeSH ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sommerfeld Identity
Arnold Johannes Wilhelm Sommerfeld (; 5 December 1868 – 26 April 1951) was a German theoretical physicist who pioneered developments in atomic and quantum physics, and also educated and mentored many students for the new era of theoretical physics. He served as doctoral advisor and postdoc advisor to seven Nobel Prize winners and supervised at least 30 other famous physicists and chemists. Only J. J. Thomson's record of mentorship offers a comparable list of high-achieving students. He introduced the second quantum number, azimuthal quantum number, and the third quantum number, magnetic quantum number. He also introduced the fine-structure constant and pioneered X-ray wave theory. Early life and education Sommerfeld was born in 1868 to a family with deep ancestral roots in Prussia. His mother Cäcilie Matthias (1839–1902) was the daughter of a Potsdam builder. His father Franz Sommerfeld (1820–1906) was a physician from a leading family in Königsberg, where Arnold's gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |