|
Best Rational Approximation
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In a finite continued fraction (or terminated continued fraction), the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers a_i are called the coefficients or terms of the continued fraction. It is generally assumed that the numerator of all of the fractions is 1. If arbitrary values and/or functions are used in place of one or more of the numerators or the integers in the denominators, the resulting expression is a generalized continued fraction. When it is necessary t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prefix (computer Science)
In formal language theory and computer science, a substring is a contiguous sequence of characters within a string. For instance, "''the best of''" is a substring of "''It was the best of times''". In contrast, "''Itwastimes''" is a subsequence of "''It was the best of times''", but not a substring. Prefixes and suffixes are special cases of substrings. A prefix of a string S is a substring of S that occurs at the beginning of S; likewise, a suffix of a string S is a substring that occurs at the end of S. The substrings of the string "''apple''" would be: "''a''", "''ap''", "''app''", "''appl''", "''apple''", "''p''", "''pp''", "''ppl''", "''pple''", "''pl''", "''ple''", "''l''", "''le''" "''e''", "" (note the empty string at the end). Substring A string u is a substring (or factor) of a string t if there exists two strings p and s such that t = pus. In particular, the empty string is a substring of every string. Example: The string u=ana is equal to substrings (and subse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
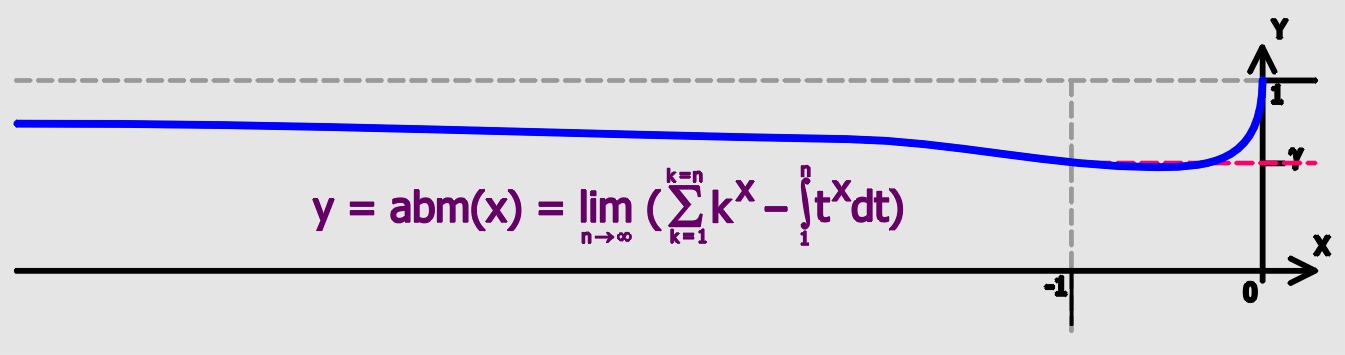
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
A Property Of The Golden Ratio φ
A, or a, is the first letter and the first vowel of the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is ''a'' (pronounced ), plural ''aes''. It is similar in shape to the Ancient Greek letter alpha, from which it derives. The uppercase version consists of the two slanting sides of a triangle, crossed in the middle by a horizontal bar. The lowercase version can be written in two forms: the double-storey a and single-storey ɑ. The latter is commonly used in handwriting and fonts based on it, especially fonts intended to be read by children, and is also found in italic type. In English grammar, " a", and its variant " an", are indefinite articles. History The earliest certain ancestor of "A" is aleph (also written 'aleph), the first letter of the Phoenician alphabet, which consisted entirely of consonants (for that reason, it is also called an abjad to distinguish it fro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0, where the Greek letter phi ( or \phi) denotes the golden ratio. The constant \varphi satisfies the quadratic equation \varphi^2 = \varphi + 1 and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli, and also goes by several other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of \varphi—may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has been used to analyze the proportions of natural object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
E (mathematical Constant)
The number , also known as Euler's number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of the natural logarithms. It is the limit of as approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite series e = \sum\limits_^ \frac = 1 + \frac + \frac + \frac + \cdots. It is also the unique positive number such that the graph of the function has a slope of 1 at . The (natural) exponential function is the unique function that equals its own derivative and satisfies the equation ; hence one can also define as . The natural logarithm, or logarithm to base , is the inverse function to the natural exponential function. The natural logarithm of a number can be defined directly as the area under the curve between and , in which case is the value of for which this area equals one (see image). There are various other characteriz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irrational Number
In mathematics, the irrational numbers (from in- prefix assimilated to ir- (negative prefix, privative) + rational) are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being '' incommensurable'', meaning that they share no "measure" in common, that is, there is no length ("the measure"), no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself. Among irrational numbers are the ratio of a circle's circumference to its diameter, Euler's number ''e'', the golden ratio ''φ'', and the square root of two. In fact, all square roots of natural numbers, other than of perfect squares, are irrational. Like all real numbers, irrational numbers can be expressed in positional notation, notably as a decimal number. In the cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplicative Inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when Multiplication, multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a rational number, fraction ''a''/''b'' is ''b''/''a''. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the Function (mathematics), function ''f''(''x'') that maps ''x'' to 1/''x'', is one of the simplest examples of a function which is its own inverse (an Involution (mathematics), involution). Multiplying by a number is the same as Division (mathematics), dividing by its reciprocal and vice versa. For example, multiplication by 4/5 (or 0.8) will give the same result as division by 5/4 (or 1.25). Therefore, multiplication by a number followed by multiplication by its reciprocal yiel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floor And Ceiling Functions
In mathematics and computer science, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least integer greater than or equal to , denoted or . For example, , , , and . Historically, the floor of has been–and still is–called the integral part or integer part of , often denoted (as well as a variety of other notations). Some authors may define the integral part as if is nonnegative, and otherwise: for example, and . The operation of truncation generalizes this to a specified number of digits: truncation to zero significant digits is the same as the integer part. For an integer, . Notation The ''integral part'' or ''integer part'' of a number ( in the original) was first defined in 1798 by Adrien-Marie Legendre in his proof of the Legendre's formula. Carl Friedrich Gauss introduced the square bracket notation in his ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation
An approximation is anything that is intentionally similar but not exactly equality (mathematics), equal to something else. Etymology and usage The word ''approximation'' is derived from Latin ''approximatus'', from ''proximus'' meaning ''very near'' and the prefix ''ad-'' (''ad-'' before ''p'' becomes ap- by assimilation (phonology), assimilation) meaning ''to''. Words like ''approximate'', ''approximately'' and ''approximation'' are used especially in technical or scientific contexts. In everyday English, words such as ''roughly'' or ''around'' are used with a similar meaning. It is often found abbreviated as ''approx.'' The term can be applied to various properties (e.g., value, quantity, image, description) that are nearly, but not exactly correct; similar, but not exactly the same (e.g., the approximate time was 10 o'clock). Although approximation is most often applied to numbers, it is also frequently applied to such things as Function (mathematics), mathematical functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Rational Functions
In mathematics, the Chebyshev rational functions are a sequence of functions which are both rational and orthogonal. They are named after Pafnuty Chebyshev. A rational Chebyshev function of degree is defined as: :R_n(x)\ \stackrel\ T_n\left(\frac\right) where is a Chebyshev polynomial of the first kind. Properties Many properties can be derived from the properties of the Chebyshev polynomials of the first kind. Other properties are unique to the functions themselves. Recursion :R_(x)=2\,\fracR_n(x)-R_(x) \quad \text n\ge 1 Differential equations :(x+1)^2R_n(x)=\frac\fracR_(x)-\frac\fracR_(x) \quad \text n\ge 2 :(x+1)^2x\fracR_n(x)+\frac\fracR_n(x)+n^2R_(x) = 0 Orthogonality Defining: :\omega(x) \ \stackrel\ \frac The orthogonality of the Chebyshev rational functions may be written: :\int_^\infty R_m(x)\,R_n(x)\,\omega(x)\,\mathrmx=\frac\delta_ where for and for ; is the Kronecker delta In mathematics, the Kronecker delta (named after Leopold Krone ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |