|
Bandlimited
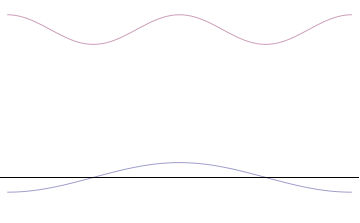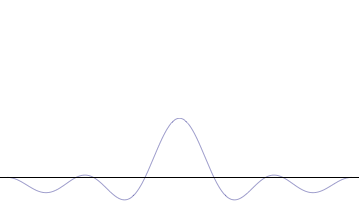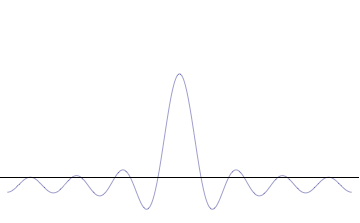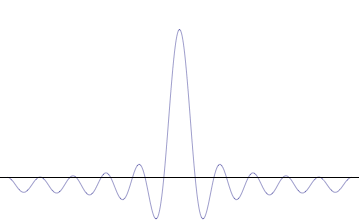
Bandlimiting is the limiting of a signal's frequency domain representation or spectral density to zero above a certain finite frequency. A band-limited signal is one whose Fourier transform or spectral density has bounded support. A bandlimited signal may be either random (stochastic) or non-random (deterministic). In general, infinitely many terms are required in a continuous Fourier series representation of a signal, but if a finite number of Fourier series terms can be calculated from that signal, that signal is considered to be band-limited. Sampling bandlimited signals A bandlimited signal can be fully reconstructed from its samples, provided that the sampling rate exceeds twice the maximum frequency in the bandlimited signal. This minimum sampling rate is called the Nyquist rate. This result, usually attributed to Nyquist and Shannon, is known as the Nyquist–Shannon sampling theorem. An example of a simple deterministic bandlimited signal is a sinusoid of the form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bandlimited
Bandlimiting is the limiting of a signal's frequency domain representation or spectral density to zero above a certain finite frequency. A band-limited signal is one whose Fourier transform or spectral density has bounded support. A bandlimited signal may be either random (stochastic) or non-random (deterministic). In general, infinitely many terms are required in a continuous Fourier series representation of a signal, but if a finite number of Fourier series terms can be calculated from that signal, that signal is considered to be band-limited. Sampling bandlimited signals A bandlimited signal can be fully reconstructed from its samples, provided that the sampling rate exceeds twice the maximum frequency in the bandlimited signal. This minimum sampling rate is called the Nyquist rate. This result, usually attributed to Nyquist and Shannon, is known as the Nyquist–Shannon sampling theorem. An example of a simple deterministic bandlimited signal is a sinusoid of the form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist–Shannon Sampling Theorem
The Nyquist–Shannon sampling theorem is a theorem in the field of signal processing which serves as a fundamental bridge between continuous-time signals and discrete-time signals. It establishes a sufficient condition for a sample rate that permits a discrete sequence of ''samples'' to capture all the information from a continuous-time signal of finite bandwidth. Strictly speaking, the theorem only applies to a class of mathematical functions having a Fourier transform that is zero outside of a finite region of frequencies. Intuitively we expect that when one reduces a continuous function to a discrete sequence and interpolates back to a continuous function, the fidelity of the result depends on the density (or sample rate) of the original samples. The sampling theorem introduces the concept of a sample rate that is sufficient for perfect fidelity for the class of functions that are band-limited to a given bandwidth, such that no actual information is lost in the sampling proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist Rate
In signal processing, the Nyquist rate, named after Harry Nyquist, is a value (in units of samples per second or hertz, Hz) equal to twice the highest frequency (bandwidth) of a given function or signal. When the function is digitized at a higher sample rate (see ), the resulting discrete-time sequence is said to be free of the distortion known as aliasing. Conversely, for a given sample-rate the corresponding Nyquist frequency in Hz is one-half the sample-rate. Note that the ''Nyquist rate'' is a property of a continuous-time signal, whereas ''Nyquist frequency'' is a property of a discrete-time system. The term ''Nyquist rate'' is also used in a different context with units of symbols per second, which is actually the field in which Harry Nyquist was working. In that context it is an upper bound for the symbol rate across a bandwidth-limited baseband channel such as a telegraph line or passband channel such as a limited radio frequency band or a frequency division mult ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Density
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of a certain signal or sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The power spectral density (PSD) then refers to the spectral energy distribution that would be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncertainty Principle
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, ''x'', and momentum, ''p'', can be predicted from initial conditions. Such variable pairs are known as complementary variables or canonically conjugate variables; and, depending on interpretation, the uncertainty principle limits to what extent such conjugate properties maintain their approximate meaning, as the mathematical framework of quantum physics does not support the notion of simultaneously well-defined conjugate properties expressed by a single value. The uncertainty principle implies that it is in general not possible to predict the value of a quantity with arbitrary certainty, even if all initial conditions are specified. Introduced first in 1927 by the German physicist Werner ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Whittaker–Shannon Interpolation Formula
The Whittaker–Shannon interpolation formula or sinc interpolation is a method to construct a continuous-time bandlimited function from a sequence of real numbers. The formula dates back to the works of E. Borel in 1898, and E. T. Whittaker in 1915, and was cited from works of J. M. Whittaker in 1935, and in the formulation of the Nyquist–Shannon sampling theorem by Claude Shannon in 1949. It is also commonly called Shannon's interpolation formula and Whittaker's interpolation formula. E. T. Whittaker, who published it in 1915, called it the Cardinal series. Definition Given a sequence of real numbers, ''x'' 'n'' the continuous function :x(t) = \sum_^ x \, \left(\frac\right)\, (where "sinc" denotes the normalized sinc function) has a Fourier transform, ''X''(''f''), whose non-zero values are confined to the region , ''f'', ≤ 1/(2''T''). When the parameter ''T'' has units of seconds, the bandlimit, 1/(2''T''), has units of cycles/sec (hertz). When the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gabor Limit
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, ''x'', and momentum, ''p'', can be predicted from initial conditions. Such variable pairs are known as complementary variables or canonically conjugate variables; and, depending on interpretation, the uncertainty principle limits to what extent such conjugate properties maintain their approximate meaning, as the mathematical framework of quantum physics does not support the notion of simultaneously well-defined conjugate properties expressed by a single value. The uncertainty principle implies that it is in general not possible to predict the value of a quantity with arbitrary certainty, even if all initial conditions are specified. Introduced first in 1927 by the German physicist Werner Hei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deterministic
Determinism is a philosophical view, where all events are determined completely by previously existing causes. Deterministic theories throughout the history of philosophy have developed from diverse and sometimes overlapping motives and considerations. The opposite of determinism is some kind of indeterminism (otherwise called nondeterminism) or randomness. Determinism is often contrasted with free will, although some philosophers claim that the two are compatible.For example, see Determinism is often used to mean ''causal determinism'', which in physics is known as cause-and-effect. This is the concept that events within a given paradigm are bound by causality in such a way that any state of an object or event is completely determined by its prior states. This meaning can be distinguished from other varieties of determinism mentioned below. Debates about determinism often concern the scope of determined systems; some maintain that the entire universe is a single determinate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Support (mathematics)
In mathematics, the support of a real-valued function f is the subset of the function domain containing the elements which are not mapped to zero. If the domain of f is a topological space, then the support of f is instead defined as the smallest closed set containing all points not mapped to zero. This concept is used very widely in mathematical analysis. Formulation Suppose that f : X \to \R is a real-valued function whose domain is an arbitrary set X. The of f, written \operatorname(f), is the set of points in X where f is non-zero: \operatorname(f) = \. The support of f is the smallest subset of X with the property that f is zero on the subset's complement. If f(x) = 0 for all but a finite number of points x \in X, then f is said to have . If the set X has an additional structure (for example, a topology), then the support of f is defined in an analogous way as the smallest subset of X of an appropriate type such that f vanishes in an appropriate sense on its complement. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time–frequency Analysis
In signal processing, time–frequency analysis comprises those techniques that study a signal in both the time and frequency domains ''simultaneously,'' using various time–frequency representations. Rather than viewing a 1-dimensional signal (a function, real or complex-valued, whose domain is the real line) and some transform (another function whose domain is the real line, obtained from the original via some transform), time–frequency analysis studies a two-dimensional signal – a function whose domain is the two-dimensional real plane, obtained from the signal via a time–frequency transform. The mathematical motivation for this study is that functions and their transform representation are tightly connected, and they can be understood better by studying them jointly, as a two-dimensional object, rather than separately. A simple example is that the 4-fold periodicity of the Fourier transform – and the fact that two-fold Fourier transform reverses direction – can be int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. Variance is an important tool in the sciences, where statistical analysis of data is common. The variance is the square of the standard deviation, the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.jpg)

