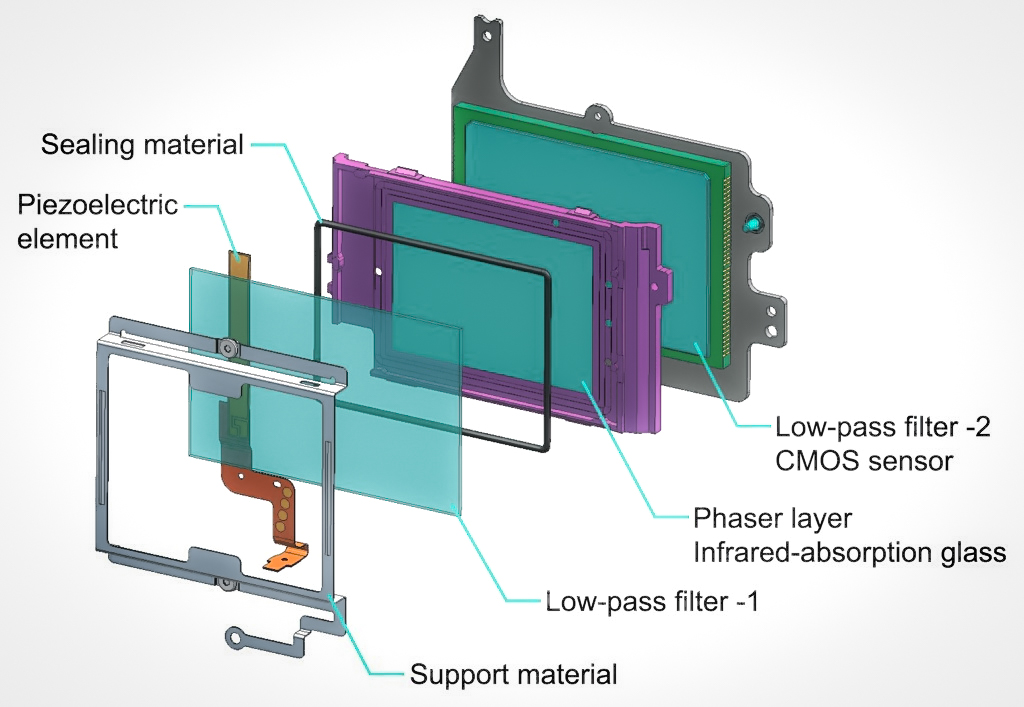
|
Whittaker–Shannon Interpolation Formula
The Whittaker–Shannon interpolation formula or sinc interpolation is a method to construct a continuous-time bandlimited function from a sequence of real numbers. The formula dates back to the works of E. Borel in 1898, and E. T. Whittaker in 1915, and was cited from works of J. M. Whittaker in 1935, and in the formulation of the Nyquist–Shannon sampling theorem by Claude Shannon in 1949. It is also commonly called Shannon's interpolation formula and Whittaker's interpolation formula. E. T. Whittaker, who published it in 1915, called it the Cardinal series. Definition Given a sequence of real numbers, ''x'' 'n''''x''(''nT''), the continuous function :x(t) = \sum_^ x \, \left(\frac\right)\, (where "sinc" denotes the normalized sinc function) has a Fourier transform, ''X''(''f''), whose non-zero values are confined to the region :, f, \le \frac. When the parameter ''T'' has units of seconds, the bandlimit, 1/(2''T''), has units of cycles/sec (hertz). When the ''x'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous-time
In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which variables that evolve over time are modeled. Discrete time Discrete time views values of variables as occurring at distinct, separate "points in time", or equivalently as being unchanged throughout each non-zero region of time ("time period")—that is, time is viewed as a discrete variable. Thus a non-time variable jumps from one value to another as time moves from one time period to the next. This view of time corresponds to a digital clock that gives a fixed reading of 10:37 for a while, and then jumps to a new fixed reading of 10:38, etc. In this framework, each variable of interest is measured once at each time period. The number of measurements between any two time periods is finite. Measurements are typically made at sequential integer values of the variable "time". A discrete signal or discrete-time signal is a time series consisting of a sequence of quantities. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Convergence
In the mathematical field of analysis, uniform convergence is a mode of convergence of functions stronger than pointwise convergence. A sequence of functions (f_n) converges uniformly to a limiting function f on a set E as the function domain if, given any arbitrarily small positive number \varepsilon, a number N can be found such that each of the functions f_N, f_,f_,\ldots differs from f by no more than \varepsilon ''at every point'' x ''in'' E. Described in an informal way, if f_n converges to f uniformly, then how quickly the functions f_n approach f is "uniform" throughout E in the following sense: in order to guarantee that f_n(x) differs from f(x) by less than a chosen distance \varepsilon, we only need to make sure that n is larger than or equal to a certain N, which we can find without knowing the value of x\in E in advance. In other words, there exists a number N=N(\varepsilon) that could depend on \varepsilon but is ''independent of x'', such that choosing n\geq N wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinc Filter
In signal processing, a sinc filter can refer to either a sinc-in-time filter whose impulse response is a sinc function and whose frequency response is rectangular, or to a sinc-in-frequency filter whose impulse response is rectangular and whose frequency response is a sinc function. Calling them according to which domain the filter resembles a sinc avoids confusion. If the domain is unspecified, sinc-in-time is often assumed, or context hopefully can infer the correct domain. Sinc-in-time Sinc-in-time is an ideal filter that removes all frequency components above a given cutoff frequency, without attenuating lower frequencies, and has linear phase response. It may thus be considered a ''brick-wall filter'' or ''rectangular filter.'' Its impulse response is a sinc function in the time domain: \frac while its frequency response is a rectangular function: :H(f) = \operatorname \left( \frac \right) = \begin 0, & \text , f, > B, \\ \frac, & \text , f, = B, \\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinc Function
In mathematics, physics and engineering, the sinc function ( ), denoted by , has two forms, normalized and unnormalized.. In mathematics, the historical unnormalized sinc function is defined for by \operatorname(x) = \frac. Alternatively, the unnormalized sinc function is often called the sampling function, indicated as Sa(''x''). In digital signal processing and information theory, the normalized sinc function is commonly defined for by \operatorname(x) = \frac. In either case, the value at is defined to be the limiting value \operatorname(0) := \lim_\frac = 1 for all real (the limit can be proven using the squeeze theorem). The normalization causes the definite integral of the function over the real numbers to equal 1 (whereas the same integral of the unnormalized sinc function has a value of ). As a further useful property, the zeros of the normalized sinc function are the nonzero integer values of . The normalized sinc function is the Fourier transform of the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal (electronics)
A signal is both the process and the result of transmission of data over some media accomplished by embedding some variation. Signals are important in multiple subject fields including signal processing, information theory and biology. In signal processing, a signal is a function that conveys information about a phenomenon. Any quantity that can vary over space or time can be used as a signal to share messages between observers. The '' IEEE Transactions on Signal Processing'' includes audio, video, speech, image, sonar, and radar as examples of signals. A signal may also be defined as observable change in a quantity over space or time (a time series), even if it does not carry information. In nature, signals can be actions done by an organism to alert other organisms, ranging from the release of plant chemicals to warn nearby plants of a predator, to sounds or motions made by animals to alert other animals of food. Signaling occurs in all organisms even at cellular level ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sampling (signal Processing)
In signal processing, sampling is the reduction of a continuous-time signal to a discrete-time signal. A common example is the conversion of a sound wave to a sequence of "samples". A sample is a value of the signal at a point in time and/or space; this definition differs from the term's usage in statistics, which refers to a set of such values. A sampler is a subsystem or operation that extracts samples from a continuous signal. A theoretical ideal sampler produces samples equivalent to the instantaneous value of the continuous signal at the desired points. The original signal can be reconstructed from a sequence of samples, up to the Nyquist limit, by passing the sequence of samples through a reconstruction filter. Theory Functions of space, time, or any other dimension can be sampled, and similarly in two or more dimensions. For functions that vary with time, let s(t) be a continuous function (or "signal") to be sampled, and let sampling be performed by measuring ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectangular Function
The rectangular function (also known as the rectangle function, rect function, Pi function, Heaviside Pi function, gate function, unit pulse, or the normalized boxcar function) is defined as \operatorname\left(\frac\right) = \Pi\left(\frac\right) = \left\{\begin{array}{rl} 0, & \text{if } , t, > \frac{a}{2} \\ \frac{1}{2}, & \text{if } , t, = \frac{a}{2} \\ 1, & \text{if } , t, \frac{1}{2} \\ \frac{1}{2} & \mbox{if } , t, = \frac{1}{2} \\ 1 & \mbox{if } , t, < \frac{1}{2}. \\ \end{cases} Dirac delta function The rectangle function can be used to represent the . Specifically,For a function , its average over the w ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Anti-aliasing
In digital signal processing, spatial anti-aliasing is a technique for minimizing the distortion artifacts (aliasing) when representing a high-resolution image at a lower resolution. Anti-aliasing is used in digital photography, computer graphics, digital audio, and many other applications. Anti-aliasing means removing signal components that have a higher frequency than is able to be properly resolved by the recording (or sampling) device. This removal is done before (re)sampling at a lower resolution. When sampling is performed without removing this part of the signal, it causes undesirable artifacts such as black-and-white noise. In signal acquisition and audio, anti-aliasing is often done using an analog anti-aliasing filter to remove the out-of-band component of the input signal prior to sampling with an analog-to-digital converter. In digital photography, optical anti-aliasing filters made of birefringent materials smooth the signal in the spatial optical domain. The anti-a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anti-aliasing Filter
An anti-aliasing filter (AAF) is a filter used before a signal sampler to restrict the bandwidth of a signal to satisfy the Nyquist–Shannon sampling theorem over the band of interest. Since the theorem states that unambiguous reconstruction of the signal from its samples is possible when the power of frequencies above the Nyquist frequency is zero, a brick wall filter is an idealized but impractical AAF. A practical AAF makes a trade off between reduced bandwidth and increased aliasing. A practical anti-aliasing filter will typically permit some aliasing to occur or attenuate or otherwise distort some in-band frequencies close to the Nyquist limit. For this reason, many practical systems sample higher than would be theoretically required by a perfect AAF in order to ensure that all frequencies of interest can be reconstructed, a practice called oversampling. Optical applications In the case of optical image sampling, as by image sensors in digital cameras, the anti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiener–Khinchin Theorem
In applied mathematics, the Wiener–Khinchin theorem or Wiener–Khintchine theorem, also known as the Wiener–Khinchin–Einstein theorem or the Khinchin–Kolmogorov theorem, states that the autocorrelation function of a wide-sense-stationary random process has a spectral decomposition given by the power spectral density of that process. History Norbert Wiener proved this theorem for the case of a deterministic function in 1930; Aleksandr Khinchin later formulated an analogous result for stationary stochastic processes and published that probabilistic analogue in 1934. Albert Einstein explained, without proofs, the idea in a brief two-page memo in 1914. Continuous-time process For continuous time, the Wiener–Khinchin theorem says that if x is a wide-sense-stationary random process whose autocorrelation function (sometimes called autocovariance) defined in terms of statistical expected value r_(\tau) = \mathbb\big (t)^* x(t - \tau)\big< \infty, \quad \forall \tau,t \i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Density
In signal processing, the power spectrum S_(f) of a continuous time signal x(t) describes the distribution of power into frequency components f composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of any sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (PSD, or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The PSD then refers to the spectral energy distribution that would be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autocorrelation Function
Autocorrelation, sometimes known as serial correlation in the discrete time case, measures the correlation of a signal with a delayed copy of itself. Essentially, it quantifies the similarity between observations of a random variable at different points in time. The analysis of autocorrelation is a mathematical tool for identifying repeating patterns or hidden periodicities within a signal obscured by noise. Autocorrelation is widely used in signal processing, time domain and time series analysis to understand the behavior of data over time. Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance. Various time series models incorporate autocorrelation, such as unit root processes, trend-stationary processes, autoregressive processes, and moving average processes. Autocorrelation of stochastic processes In statistics, the autocorrelation of a real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |