|
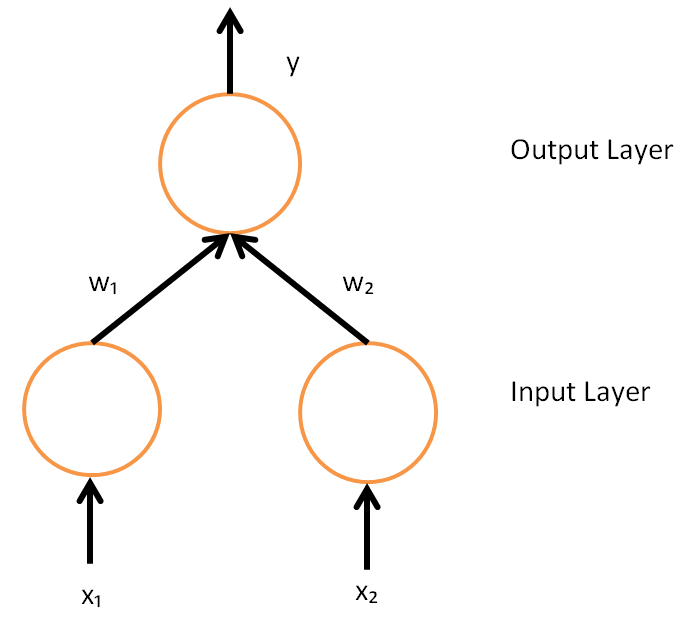
Back Propagation
In machine learning, backpropagation is a gradient computation method commonly used for training a neural network to compute its parameter updates. It is an efficient application of the chain rule to neural networks. Backpropagation computes the gradient of a loss function with respect to the weights of the network for a single input–output example, and does so efficiently, computing the gradient one layer at a time, iterating backward from the last layer to avoid redundant calculations of intermediate terms in the chain rule; this can be derived through dynamic programming. Strictly speaking, the term ''backpropagation'' refers only to an algorithm for efficiently computing the gradient, not how the gradient is used; but the term is often used loosely to refer to the entire learning algorithm – including how the gradient is used, such as by stochastic gradient descent, or as an intermediate step in a more complicated optimizer, such as Adaptive Moment Estimation. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Monte Carlo Tree Search
In computer science, Monte Carlo tree search (MCTS) is a heuristic search algorithm for some kinds of decision processes, most notably those employed in software that plays board games. In that context MCTS is used to solve the game tree. MCTS was combined with neural networks in 2016 and has been used in multiple board games like Chess, Shogi, Checkers, Backgammon, Contract Bridge, Go, Scrabble, and Clobber as well as in turn-based-strategy video games (such as Total War: Rome II's implementation in the high level campaign AI) and applications outside of games. History Monte Carlo method The Monte Carlo method, which uses random sampling for deterministic problems which are difficult or impossible to solve using other approaches, dates back to the 1940s. In his 1987 PhD thesis, Bruce Abramson combined minimax search with an ''expected-outcome model'' based on random game playouts to the end, instead of the usual static evaluation function. Abramson said the expected-out ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
One-hot
In digital circuits and machine learning, a one-hot is a group of bits among which the legal combinations of values are only those with a single high (1) bit and all the others low (0). A similar implementation in which all bits are '1' except one '0' is sometimes called one-cold. In statistics, dummy variables represent a similar technique for representing categorical data. Applications Digital circuitry One-hot encoding is often used for indicating the state of a state machine. When using binary, a decoder is needed to determine the state. A one-hot state machine, however, does not need a decoder as the state machine is in the ''n''th state if, and only if, the ''n''th bit is high. A ring counter with 15 sequentially ordered states is an example of a state machine. A 'one-hot' implementation would have 15 flip-flops chained in series with the Q output of each flip-flop connected to the D input of the next and the D input of the first flip-flop connected to the Q output of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Swish Function
The swish function is a family of mathematical function defined as follows: : \operatorname_\beta(x) = x \operatorname(\beta x) = \frac. where \beta can be constant (usually set to 1) or trainable and "sigmoid" refers to the logistic function. The swish family was designed to smoothly interpolate between a linear function and the ReLU function. When considering positive values, Swish is a particular case of doubly parameterized sigmoid shrinkage function defined in . Variants of the swish function include Mish. Special values For β = 0, the function is linear: f(''x'') = ''x''/2. For β = 1, the function is the Sigmoid Linear Unit (SiLU). With β → ∞, the function converges to ReLU. Thus, the swish family smoothly interpolates between a linear function and the ReLU function. Since \operatorname_\beta(x) = \operatorname_1(\beta x) / \beta, all instances of swish have the same shape as the default \operatorname_1 , zoomed by \beta . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tanh
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions are used to express the angle of parallelism in hyperbolic geometry. They are used to express Lorentz boosts as hyperbolic rotations in special relativity. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, and fluid dynamics. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Dictionary'', p. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
ReLU
In the context of Neural network (machine learning), artificial neural networks, the rectifier or ReLU (rectified linear unit) activation function is an activation function defined as the non-negative part of its argument, i.e., the ramp function: :\operatorname(x) = x^+ = \max(0, x) = \frac = \begin x & \text x > 0, \\ 0 & x \le 0 \end where x is the input to a Artificial neuron, neuron. This is analogous to half-wave rectification in electrical engineering. ReLU is one of the most popular activation functions for artificial neural networks, and finds application in computer vision and speech recognitionAndrew L. Maas, Awni Y. Hannun, Andrew Y. Ng (2014)Rectifier Nonlinearities Improve Neural Network Acoustic Models using Deep learning, deep neural nets and computational neuroscience. History The ReLU was first used by Alston Scott Householder, Alston Householder in 1941 as a mathematical abstraction of biological neural networks. Kunihiko Fukushima in 1969 used R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ramp Function
The ramp function is a unary real function, whose graph is shaped like a ramp. It can be expressed by numerous definitions, for example "0 for negative inputs, output equals input for non-negative inputs". The term "ramp" can also be used for other functions obtained by scaling and shifting, and the function in this article is the ''unit'' ramp function (slope 1, starting at 0). In mathematics, the ramp function is also known as the positive part. In machine learning, it is commonly known as a ReLU activation function or a rectifier in analogy to half-wave rectification in electrical engineering. In statistics (when used as a likelihood function) it is known as a tobit model. This function has numerous applications in mathematics and engineering, and goes by various names, depending on the context. There are differentiable variants of the ramp function. Definitions The ramp function () may be defined analytically in several ways. Possible definitions are: * A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rectifier (neural Networks)
In the context of Neural network (machine learning), artificial neural networks, the rectifier or ReLU (rectified linear unit) activation function is an activation function defined as the non-negative part of its argument, i.e., the ramp function: :\operatorname(x) = x^+ = \max(0, x) = \frac = \begin x & \text x > 0, \\ 0 & x \le 0 \end where x is the input to a Artificial neuron, neuron. This is analogous to half-wave rectification in electrical engineering. ReLU is one of the most popular activation functions for artificial neural networks, and finds application in computer vision and speech recognitionAndrew L. Maas, Awni Y. Hannun, Andrew Y. Ng (2014)Rectifier Nonlinearities Improve Neural Network Acoustic Models using Deep learning, deep neural nets and computational neuroscience. History The ReLU was first used by Alston Scott Householder, Alston Householder in 1941 as a mathematical abstraction of biological neural networks. Kunihiko Fukushima in 1969 used R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sigmoid Function
A sigmoid function is any mathematical function whose graph of a function, graph has a characteristic S-shaped or sigmoid curve. A common example of a sigmoid function is the logistic function, which is defined by the formula :\sigma(x) = \frac = \frac = 1 - \sigma(-x). Other sigmoid functions are given in the #Examples, Examples section. In some fields, most notably in the context of artificial neural networks, the term "sigmoid function" is used as a synonym for "logistic function". Special cases of the sigmoid function include the Gompertz curve (used in modeling systems that saturate at large values of ''x'') and the ogee curve (used in the spillway of some dams). Sigmoid functions have domain of all real numbers, with return (response) value commonly monotonically increasing but could be decreasing. Sigmoid functions most often show a return value (''y'' axis) in the range 0 to 1. Another commonly used range is from −1 to 1. A wide variety of sigmoid functions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Softmax Function
The softmax function, also known as softargmax or normalized exponential function, converts a tuple of real numbers into a probability distribution of possible outcomes. It is a generalization of the logistic function to multiple dimensions, and is used in multinomial logistic regression. The softmax function is often used as the last activation function of a neural network to normalize the output of a network to a probability distribution over predicted output classes. Definition The softmax function takes as input a tuple of real numbers, and normalizes it into a probability distribution consisting of probabilities proportional to the exponentials of the input numbers. That is, prior to applying softmax, some tuple components could be negative, or greater than one; and might not sum to 1; but after applying softmax, each component will be in the interval (0, 1), and the components will add up to 1, so that they can be interpreted as probabilities. Furthermore, the la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Logistic Function
A logistic function or logistic curve is a common S-shaped curve ( sigmoid curve) with the equation f(x) = \frac where The logistic function has domain the real numbers, the limit as x \to -\infty is 0, and the limit as x \to +\infty is L. The exponential function with negated argument (e^ ) is used to define the standard logistic function, depicted at right, where L=1, k=1, x_0=0, which has the equation f(x) = \frac and is sometimes simply called the sigmoid. It is also sometimes called the expit, being the inverse function of the logit. The logistic function finds applications in a range of fields, including biology (especially ecology), biomathematics, chemistry, demography, economics, geoscience, mathematical psychology, probability, sociology, political science, linguistics, statistics, and artificial neural networks. There are various generalizations, depending on the field. History The logistic function was introduced in a series of three papers by Pier ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Activation Function
The activation function of a node in an artificial neural network is a function that calculates the output of the node based on its individual inputs and their weights. Nontrivial problems can be solved using only a few nodes if the activation function is ''nonlinear''. Modern activation functions include the logistic ( sigmoid) function used in the 2012 speech recognition model developed by Hinton et al; the ReLU used in the 2012 AlexNet computer vision model and in the 2015 ResNet model; and the smooth version of the ReLU, the GELU, which was used in the 2018 BERT model. Comparison of activation functions Aside from their empirical performance, activation functions also have different mathematical properties: ; Nonlinear: When the activation function is non-linear, then a two-layer neural network can be proven to be a universal function approximator. This is known as the Universal Approximation Theorem. The identity activation function does not satisfy this property. W ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Squared Error Loss
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economics, for example, this is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |