|
Bitruncated 5-orthoplex
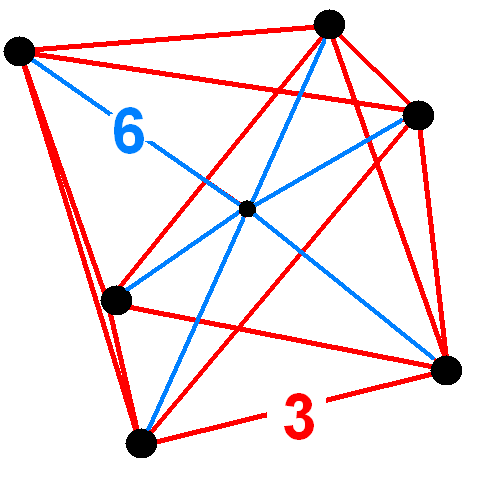
In five-dimensional geometry, a truncated 5-orthoplex is a convex uniform 5-polytope, being a truncation of the regular 5-orthoplex. There are 4 unique truncations of the 5-orthoplex. Vertices of the truncation 5-orthoplex are located as pairs on the edge of the 5-orthoplex. Vertices of the bitruncated 5-orthoplex are located on the triangular faces of the 5-orthoplex. The third and fourth truncations are more easily constructed as second and first truncations of the 5-cube. Truncated 5-orthoplex Alternate names * Truncated pentacross * Truncated triacontiditeron (Acronym: tot) (Jonathan Bowers) Coordinates Cartesian coordinates for the vertices of a truncated 5-orthoplex, centered at the origin, are all 80 vertices are sign (4) and coordinate (20) permutations of : (±2,±1,0,0,0) Images The truncated 5-orthoplex is constructed by a truncation operation applied to the 5-orthoplex. All edges are shortened, and two new vertices are added on each original edge. Bi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
5-cube T4
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces. It is represented by Schläfli symbol or , constructed as 3 tesseracts, , around each cubic ridge. It can be called a penteract, a portmanteau of the Greek word , for 'five' (dimensions), and the word ''tesseract'' (the 4-cube). It can also be called a regular deca-5-tope or decateron, being a 5-dimensional polytope constructed from 10 regular facets. Related polytopes It is a part of an infinite hypercube family. The dual of a 5-cube is the 5-orthoplex, of the infinite family of orthoplexes. Applying an '' alternation'' operation, deleting alternating vertices of the 5-cube, creates another uniform 5-polytope, called a 5-demicube, which is also part of an infinite family called the demihypercubes. The 5-cube can be seen as an ''order-3 tesseractic honeycomb'' on a 4-sphere. It is related to the Euclide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform 5-polytope
In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope Facet (geometry), facets. The complete set of convex uniform 5-polytopes has not been determined, but many can be made as Wythoff constructions from a small set of Coxeter groups, symmetry groups. These construction operations are represented by the permutations of rings of the Coxeter diagrams. History of discovery *Regular polytopes: (convex faces) **1852: Ludwig Schläfli proved in his manuscript ''Theorie der vielfachen Kontinuität'' that there are exactly 3 regular polytopes in 5 or more dimensions. *Convex semiregular polytopes: (Various definitions before Coxeter's uniform category) **1900: Thorold Gosset enumerated the list of nonprismatic semiregular convex polytopes with regular facets (convex regular 4-polytopes) in his publication ''On the Regular and Semi-Regular Figures in Space of n Dimension ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitruncation
In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves. Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation or In regular polyhedra and tilings For regular polyhedra (i.e. regular 3-polytopes), a ''bitruncated'' form is the truncated dual. For example, a bitruncated cube is a truncated octahedron. In regular 4-polytopes and honeycombs For a regular 4-polytope, a ''bitruncated'' form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual, and will have double the symmetry if the original 4-polytope is self-dual. A regular polytope (or honeycomb) will have its cells bitruncated into truncated cells, and the vertices are replaced by truncated cells. Self-dual 4-polytope/honeycombs An interesting result of this operation is that self- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tritruncated 5-cubic Honeycomb
In geometry, the 5-cubic honeycomb or penteractic honeycomb is the only regular space-filling tessellation (or honeycomb) in Euclidean 5-space. Four 5-cubes meet at each cubic cell, and it is more explicitly called an ''order-4 penteractic honeycomb''. It is analogous to the square tiling of the plane and to the cubic honeycomb of 3-space, and the tesseractic honeycomb of 4-space. Constructions There are many different Wythoff constructions of this honeycomb. The most symmetric form is regular, with Schläfli symbol . Another form has two alternating 5-cube facets (like a checkerboard) with Schläfli symbol . The lowest symmetry Wythoff construction has 32 types of facets around each vertex and a prismatic product Schläfli symbol 5. Related polytopes and honeycombs The ,33,4 , Coxeter group generates 63 permutations of uniform tessellations, 35 with unique symmetry and 34 with unique geometry. The expanded 5-cubic honeycomb is geometrically identical to the 5-cubic hone ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tessellation
A tessellation or tiling is the covering of a surface, often a plane (mathematics), plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to high-dimensional spaces, higher dimensions and a variety of geometries. A periodic tiling has a repeating pattern. Some special kinds include ''regular tilings'' with regular polygonal tiles all of the same shape, and ''semiregular tilings'' with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called "non-periodic". An ''aperiodic tiling'' uses a small set of tile shapes that cannot form a repeating pattern. A ''tessellation of space'', also known as a space filling or honeycomb, can be defined in the geometry of higher dimensions. A real physical tessellation is a tiling made of materials such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square-pyramidal Pyramid
In 4-dimensional geometry, the octahedral pyramid is bounded by one octahedron on the base and 8 triangular pyramid cells which meet at the apex. Since an octahedron has a circumradius divided by edge length less than one, the triangular pyramids can be made with regular faces (as regular tetrahedrons) by computing the appropriate height. Having all regular cells, it is a Blind polytope. Two copies can be augmented to make an octahedral bipyramid which is also a Blind polytope. Occurrences of the octahedral pyramid The regular 16-cell has ''octahedral pyramids'' around every vertex, with the octahedron passing through the center of the 16-cell. Therefore placing two regular octahedral pyramids base to base constructs a 16-cell. The 16-cell tessellates 4-dimensional space as the 16-cell honeycomb. Exactly 24 regular octahedral pyramids will fit together around a vertex in four-dimensional space (the apex of each pyramid). This construction yields a 24-cell with octahedral boundin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
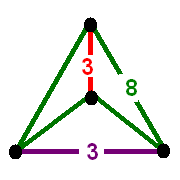
Bitruncated Pentacross Verf
In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves. Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation or In regular polyhedra and tilings For regular polyhedra (i.e. regular 3-polytopes), a ''bitruncated'' form is the truncated dual. For example, a bitruncated cube is a truncated octahedron. In regular 4-polytopes and honeycombs For a regular 4-polytope, a ''bitruncated'' form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual, and will have double the symmetry if the original 4-polytope is self-dual. A regular polytope (or honeycomb) will have its cells bitruncated into truncated cells, and the vertices are replaced by truncated cells. Self-dual 4-polytope/honeycombs An interesting result of this operation is that self-d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutation
In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements. The word "permutation" also refers to the act or process of changing the linear order of an ordered set. Permutations differ from combinations, which are selections of some members of a set regardless of order. For example, written as tuples, there are six permutations of the set , namely (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), and (3, 2, 1). These are all the possible orderings of this three-element set. Anagrams of words whose letters are different are also permutations: the letters are already ordered in the original word, and the anagram is a reordering of the letters. The study of permutations of finite sets is an important topic in the fields of combinatorics and group theory. Permutations are used in almost every branch of mathematics, and in many other fields of scie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinates
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a ''coordinate axis'' or just ''axis'' (plural ''axes'') of the system, and the point where they meet is its ''origin'', at ordered pair . The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, ''n'' Cartesian coordinates (an element of real ''n''-space) specify the point in an ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the n-dimensional Euclidean space \mathbb^n. Most texts. use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others''Mathematical Programming'', by Melvyn W. Jeter (1986) p. 68/ref> (including this article) allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary. Convex polytopes play an important role both in various branches of mathematics and in applied areas, most notably in linear programming. In the influential textbooks of Grünbaum and Ziegler on the subject, as well as in many other texts in discrete geometry, convex polytopes are often simply called "polytopes". Grünbaum points out that this is solely to avoi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example. However, not all Coxeter groups are finite, and not all can be described in terms of symmetries and Euclidean reflections. Coxeter groups were introduced in 1934 as abstractions of reflection groups , and finite Coxeter groups were classified in 1935 . Coxeter groups find applications in many areas of mathematics. Examples of finite Coxeter groups include the symmetry groups of regular polytopes, and the Weyl groups of simple Lie algebras. Examples of infinite Coxeter groups include the triangle groups corresponding to regular tessellations of the Euclidean plane and the hyperbolic plane, and the Weyl groups of infinite-dimensional Kac–Moody algebras. Standard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |