|
Algorithmically Random Set
Intuitively, an algorithmically random sequence (or random sequence) is a sequence of binary digits that appears random to any algorithm running on a (prefix-free or not) universal Turing machine. The notion can be applied analogously to sequences on any finite alphabet (e.g. decimal digits). Random sequences are key objects of study in algorithmic information theory. In measure-theoretic probability theory, introduced by Andrey Kolmogorov in 1933, there is ''no such thing'' as a random sequence. For example, consider flipping a fair coin infinitely many times. Any particular sequence, be it 0000\dots or 011010\dots, has equal probability of exactly zero. There is no way to state that one sequence is "more random" than another sequence, using the language of measure-theoretic probability. However, it is intuitively obvious that 011010\dots looks more random than 0000\dots. Algorithmic randomness theory formalizes this intuition. As different types of algorithms are sometimes co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Random Sequence
The concept of a random sequence is essential in probability theory and statistics. The concept generally relies on the notion of a sequence of random variables and many statistical discussions begin with the words "let ''X''1,...,''Xn'' be independent random variables...". Yet as D. H. Lehmer stated in 1951: "A random sequence is a vague notion... in which each term is unpredictable to the uninitiated and whose digits pass a certain number of tests traditional with statisticians". Axiomatic probability theory ''deliberately'' avoids a definition of a random sequence. Traditional probability theory does not state if a specific sequence is random, but generally proceeds to discuss the properties of random variables and stochastic sequences assuming some definition of randomness. The Bourbaki school considered the statement "let us consider a random sequence" an abuse of language. Early history Émile Borel was one of the first mathematicians to formally address randomness in 190 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Alonzo Church
Alonzo Church (June 14, 1903 – August 11, 1995) was an American computer scientist, mathematician, logician, and philosopher who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, the Church–Turing thesis, proving the unsolvability of the ''Entscheidungsproblem'' ("decision problem"), the Frege–Church ontology, and the Church–Rosser theorem. Alongside his doctoral student Alan Turing, Church is considered one of the founders of computer science. Life Alonzo Church was born on June 14, 1903, in Washington, D.C., where his father, Samuel Robbins Church, was a justice of the peace and the judge of the Municipal Court for the District of Columbia. He was the grandson of Alonzo Webster Church (1829–1909), United States Senate Librarian from 1881 to 1901, and great-grandson of Alonzo Church, a professor of Mathematics and Astronomy and 6th President of the University of Ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Prefix (computer Science)
In formal language theory and computer science, a substring is a contiguous sequence of characters within a string. For instance, "''the best of''" is a substring of "''It was the best of times''". In contrast, "''Itwastimes''" is a subsequence of "''It was the best of times''", but not a substring. Prefixes and suffixes are special cases of substrings. A prefix of a string S is a substring of S that occurs at the beginning of S; likewise, a suffix of a string S is a substring that occurs at the end of S. The substrings of the string "''apple''" would be: "''a''", "''ap''", "''app''", "''appl''", "''apple''", "''p''", "''pp''", "''ppl''", "''pple''", "''pl''", "''ple''", "''l''", "''le''" "''e''", "" (note the empty string at the end). Substring A string u is a substring (or factor) of a string t if there exists two strings p and s such that t = pus. In particular, the empty string is a substring of every string. Example: The string u=ana is equal to substrings (and sub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Martingale (probability Theory)
In probability theory, a martingale is a stochastic process in which the expected value of the next observation, given all prior observations, is equal to the most recent value. In other words, the conditional expectation of the next value, given the past, is equal to the present value. Martingales are used to model fair games, where future expected winnings are equal to the current amount regardless of past outcomes. History Originally, ''martingale (betting system), martingale'' referred to a class of betting strategy, betting strategies that was popular in 18th-century France. The simplest of these strategies was designed for a game in which the gambler wins their stake if a coin comes up heads and loses it if the coin comes up tails. The strategy had the gambler double their bet after every loss so that the first win would recover all previous losses plus win a profit equal to the original stake. As the gambler's wealth and available time jointly approach infinity, their pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kolmogorov Complexity
In algorithmic information theory (a subfield of computer science and mathematics), the Kolmogorov complexity of an object, such as a piece of text, is the length of a shortest computer program (in a predetermined programming language) that produces the object as output. It is a measure of the computational resources needed to specify the object, and is also known as algorithmic complexity, Solomonoff–Kolmogorov–Chaitin complexity, program-size complexity, descriptive complexity, or algorithmic entropy. It is named after Andrey Kolmogorov, who first published on the subject in 1963 and is a generalization of classical information theory. The notion of Kolmogorov complexity can be used to state and prove impossibility results akin to Cantor's diagonal argument, Gödel's incompleteness theorem, and Turing's halting problem. In particular, no program ''P'' computing a lower bound for each text's Kolmogorov complexity can return a value essentially larger than ''P'''s own len ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Claus-Peter Schnorr
Claus Peter Schnorr (4 August 1943 – 8 June 2025) mittelhessen-gedenkt.de, 21 June 2025 (in German). Retrieved 21 June 2025. was a German and . Life He received his Ph.D. from the University of Saarbrücken in 1966, and his |
Leonid Levin
Leonid Anatolievich Levin ( ; ; ; born November 2, 1948) is a Soviet-American mathematician and computer scientist. He is known for his work in randomness in computing, algorithmic complexity and intractability, average-case complexity, foundations of mathematics and computer science, algorithmic probability, theory of computation, and information theory. He obtained his master's degree at Moscow University in 1970 where he studied under Andrey Kolmogorov and completed the Candidate Degree academic requirements in 1972. He and Stephen Cook independently discovered the existence of NP-complete problems. This NP-completeness theorem, often called the Cook–Levin theorem, was a basis for one of the seven Millennium Prize Problems declared by the Clay Mathematics Institute with a $1,000,000 prize offered. The Cook–Levin theorem was a breakthrough in computer science and an important step in the development of the theory of computational complexity. Levin was awarded th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gregory Chaitin
Gregory John Chaitin ( ; born 25 June 1947) is an Argentina, Argentine-United States, American mathematician and computer scientist. Beginning in the late 1960s, Chaitin made contributions to algorithmic information theory and metamathematics, in particular a computer-theoretic result equivalent to Gödel's incompleteness theorem. He is considered to be one of the founders of what is today known as algorithmic (Solomonoff–Kolmogorov–Chaitin, Kolmogorov or program-size) Kolmogorov complexity, complexity together with Andrei Kolmogorov and Ray Solomonoff. Along with the works of e.g. Solomonoff, Kolmogorov, Per Martin-Löf, Martin-Löf, and Leonid Levin, algorithmic information theory became a foundational part of theoretical computer science, information theory, and mathematical logic. It is a common subject in several computer science curricula. Besides computer scientists, Chaitin's work draws attention of many philosophers and mathematicians to fundamental problems in mathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Jean-Paul Delahaye
Jean-Paul Delahaye (born 29 June 1952 in Saint-Mandé Seine) is a French computer scientist and mathematician. Career Delahaye has been a professor of computer science at the Lille University of Science and Technology since 1988 and a researcher in the school's computer sciences lab since 1983. Since 1991 he has written a monthly column in Pour la Science, the French version of Scientific American, dealing with mathematical games and recreations, logic, and computer science. He is a contributing author of the online scientific journal Interstices and a science and mathematics advisor to the Encyclopædia Britannica. Delahaye won the 1998 d'Alembert prize from the Société mathématique de France Groupe Lactalis S.A. (doing business as Lactalis) is a French multinational dairy products corporation, owned by the Besnier family and based in Laval, Mayenne, France. The company's former name was Besnier S.A. Lactalis is the largest dairy pr ... for his books and articles popu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Church–Turing Thesis
In Computability theory (computation), computability theory, the Church–Turing thesis (also known as computability thesis, the Turing–Church thesis, the Church–Turing conjecture, Church's thesis, Church's conjecture, and Turing's thesis) is a wiktionary:thesis, thesis about the nature of computable functions. It states that a function (mathematics), function on the natural numbers can be calculated by an effective method if and only if it is computable by a Turing machine. The thesis is named after American mathematician Alonzo Church and the British mathematician Alan Turing. Before the precise definition of computable function, mathematicians often used the informal term ''effectively calculable'' to describe functions that are computable by paper-and-pencil methods. In the 1930s, several independent attempts were made to formal system, formalize the notion of computability: * In 1933, Kurt Gödel, with Jacques Herbrand, formalized the definition of the class of general ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Per Martin-Löf
Per Erik Rutger Martin-Löf (; ; born 8 May 1942) is a Sweden, Swedish logician, philosopher, and mathematical statistics, mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in logic. In philosophical logic, Martin-Löf has wrestled with the philosophy of logical consequence and Edmund Husserl#Philosophy of logic and mathematics, judgment, partly inspired by the work of Franz Brentano, Brentano, Gottlob Frege, Frege, and Edmund Husserl, Husserl. In mathematical logic, Martin-Löf has been active in developing intuitionistic type theory as a constructive foundation of mathematics; Martin-Löf's work on type theory has influenced computer science. Until his retirement in 2009, Per Martin-Löf held a joint chair for Mathematics and Philosophy at Stockholm University. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
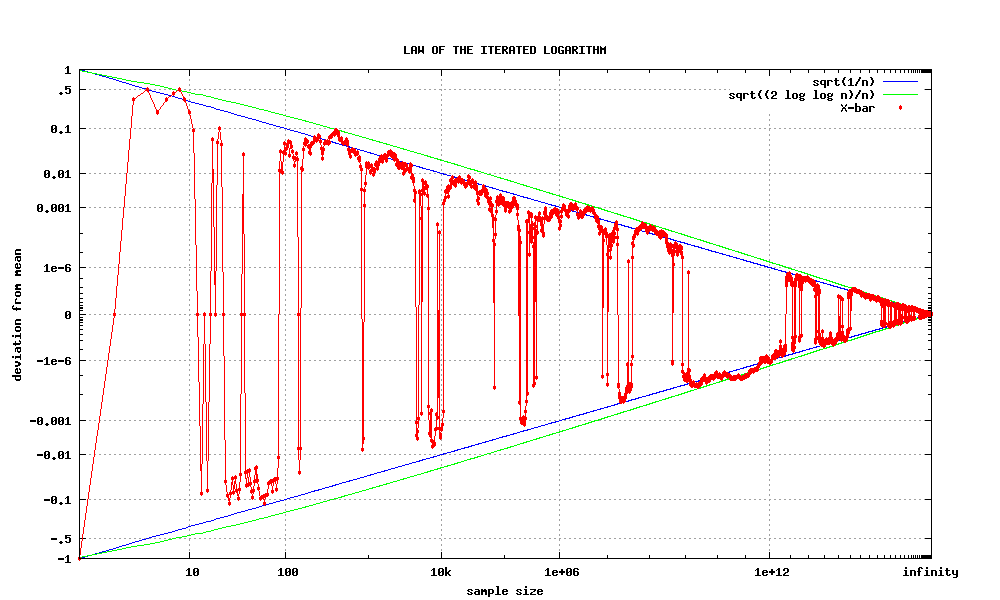
Law Of The Iterated Logarithm
In probability theory, the law of the iterated logarithm describes the magnitude of the fluctuations of a random walk. The original statement of the law of the iterated logarithm is due to Aleksandr Khinchin, A. Ya. Khinchin (1924). Another statement was given by Andrey Kolmogorov, A. N. Kolmogorov in 1929.Andrey Kolmogorov, A. Kolmogoroff"Über das Gesetz des iterierten Logarithmus" ''Mathematische Annalen'', 101: 126–135, 1929. Statement Let be independent, identically distributed random variables with zero means and unit variances. Let ''S''''n'' = ''Y''1 + ... + ''Y''''n''. Then : \limsup_ \frac = 1 \quad \text, where "log" is the natural logarithm, "lim sup" denotes the limit superior, and "a.s." stands for "almost surely". Another statement given by Andrey Kolmogorov, A. N. Kolmogorov in 1929 is as follows. Let \ be independent random variables with zero means and finite variances. Let S_n = Y_1 + \dots + Y_n and B_n = \operatorname(Y_1) + \dots + \operator ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |