|
Affine Group
In mathematics, the affine group or general affine group of any affine space over a field is the group of all invertible affine transformations from the space into itself. It is a Lie group if is the real or complex field or quaternions. Relation to general linear group Construction from general linear group Concretely, given a vector space , it has an underlying affine space obtained by "forgetting" the origin, with acting by translations, and the affine group of can be described concretely as the semidirect product of by , the general linear group of : :\operatorname(V) = V \rtimes \operatorname(V) The action of on is the natural one (linear transformations are automorphisms), so this defines a semidirect product. In terms of matrices, one writes: :\operatorname(n,K) = K^n \rtimes \operatorname(n,K) where here the natural action of on is matrix multiplication of a vector. Stabilizer of a point Given the affine group of an affine space , the stabilizer of a point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Plane
In geometry, an affine plane is a two-dimensional affine space. Examples Typical examples of affine planes are * Euclidean planes, which are affine planes over the reals equipped with a metric, the Euclidean distance. In other words, an affine plane over the reals is a Euclidean plane in which one has "forgotten" the metric (that is, one does not talk of lengths nor of angle measures). * Vector spaces of dimension two, in which the zero vector is not considered as different from the other elements * For every field or division ring ''F'', the set ''F''2 of the pairs of elements of ''F'' * The result of removing any single line (and all the points on this line) from any projective plane Coordinates and isomorphism All the affine planes defined over a field are isomorphic. More precisely, the choice of an affine coordinate system (or, in the real case, a Cartesian coordinate system) for an affine plane ''P'' over a field ''F'' induces an isomorphism of affine planes between ''P' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
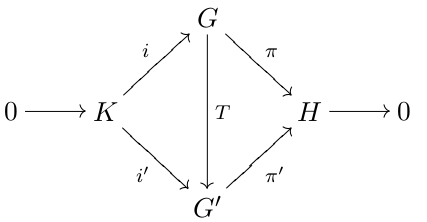
Group Extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence :1\to N\;\overset\;G\;\overset\;Q \to 1. If G is an extension of Q by N, then G is a group, \iota(N) is a normal subgroup of G and the quotient group G/\iota(N) is isomorphic to the group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined. Note that the phrasing "G is an extension of N by Q" is also used by some. Since any finite group G possesses a maximal normal subgroup N with simple factor group G/N, all finite groups may be constructed as a series of extensions with finite simple groups. This fact was a motivation for completing the classification of finite simple groups. An extension is called a central extension if the subgroup N lies in the center o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of bijective linear transformations of a vector space to itself (i.e. vector space automorphisms); in particular, they can be used to represent group elements as invertible matrices so that the group operation can be represented by matrix multiplication. In chemistry, a group representation can relate mathematical group elements to symmetric rotations and reflections of molecules. Representations of groups are important because they allow many group-theoretic problems to be reduced to problems in linear algebra, which is well understood. They are also important in physics because, for example, they describe how the symmetry group of a physical system affects the solutions of equations describing that system. The term ''representation of a group'' is also used in a more general sense to mean any "description" of a group as a group of transformations of some mathematical o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jordan Normal Form
In linear algebra, a Jordan normal form, also known as a Jordan canonical form (JCF), is an upper triangular matrix of a particular form called a Jordan matrix representing a linear operator on a finite-dimensional vector space with respect to some basis. Such a matrix has each non-zero off-diagonal entry equal to 1, immediately above the main diagonal (on the superdiagonal), and with identical diagonal entries to the left and below them. Let ''V'' be a vector space over a field ''K''. Then a basis with respect to which the matrix has the required form exists if and only if all eigenvalues of the matrix lie in ''K'', or equivalently if the characteristic polynomial of the operator splits into linear factors over ''K''. This condition is always satisfied if ''K'' is algebraically closed (for instance, if it is the field of complex numbers). The diagonal entries of the normal form are the eigenvalues (of the operator), and the number of times each eigenvalue occurs is called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Point (mathematics)
A fixed point (sometimes shortened to fixpoint, also known as an invariant point) is a value that does not change under a given transformation. Specifically, in mathematics, a fixed point of a function is an element that is mapped to itself by the function. In physics, the term fixed point can refer to a temperature that can be used as a reproducible reference point, usually defined by a phase change or triple point. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain and the codomain of , and . For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, , has no fixed points, since is never equal to for any real number. In graphical terms, a fixed point means the point is on the line , or in other words the graph of has a point in common with that line. Fixed-point iteration In numerical analysis, ''fixed-point iter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarity (geometry)
In Euclidean geometry, two objects are similar if they have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (geometry), scaling (enlarging or reducing), possibly with additional translation (geometry), translation, rotation (mathematics), rotation and reflection (mathematics), reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruence (geometry), congruent to the result of a particular uniform scaling of the other. For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other. If two angles of a triangle h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Mapping
In plane geometry, a shear mapping is a linear map that displaces each point in a fixed direction, by an amount proportional to its signed distance from the line that is parallel to that direction and goes through the origin. This type of mapping is also called shear transformation, transvection, or just shearing. An example is the mapping that takes any point with coordinates (x,y) to the point (x + 2y,y). In this case, the displacement is horizontal by a factor of 2 where the fixed line is the x-axis, and the signed distance is the y coordinate. Note that points on opposite sides of the reference line are displaced in opposite directions. Shear mappings must not be confused with rotations. Applying a shear map to a set of points of the plane will change all angles between them (except straight angles), and the length of any line segment that is not parallel to the direction of displacement. Therefore, it will usually distort the shape of a geometric figure, for example tur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate Axes
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a ''coordinate axis'' or just ''axis'' (plural ''axes'') of the system, and the point where they meet is its ''origin'', at ordered pair . The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, ''n'' Cartesian coordinates (an element of real ''n''-space) specify the point in an ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the ''perpendicular symbol'', ⟂. It can be defined between two lines (or two line segments), between a line and a plane, and between two planes. Perpendicularity is one particular instance of the more general mathematical concept of '' orthogonality''; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word "perpendicular" is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its '' normal vector''. Definitions A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a first line is perpendicular to a second line if (1) the two lines meet; and (2) at the point of intersection the straight angle on one side ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Plane
In mathematics, the Euclidean plane is a Euclidean space of dimension two. That is, a geometric setting in which two real quantities are required to determine the position of each point ( element of the plane), which includes affine notions of parallel lines, and also metrical notions of distance, circles, and angle measurement. The set \mathbb^2 of pairs of real numbers (the real coordinate plane) augmented by appropriate structure often serves as the canonical example. History Books I through IV and VI of Euclid's Elements dealt with two-dimensional geometry, developing such notions as similarity of shapes, the Pythagorean theorem (Proposition 47), equality of angles and areas, parallelism, the sum of the angles in a triangle, and the three cases in which triangles are "equal" (have the same area), among many other topics. Later, the plane was described in a so-called '' Cartesian coordinate system'', a coordinate system that specifies each point uniquely in a plane by a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |