|
Apparent Distance
Angular distance \theta (also known as angular separation, apparent distance, or apparent separation) is the angle between the two Line of sight, sightlines, or between two point objects as viewed from an observer. Angular distance appears in mathematics (in particular geometry and trigonometry) and all natural sciences (e.g. astronomy and geophysics). In the classical mechanics of rotating objects, it appears alongside angular velocity, angular acceleration, angular momentum, moment of inertia and torque. Use The term ''angular distance'' (or ''separation'') is technically synonymous with ''angle'' itself, but is meant to suggest the linear distance between objects (for instance, a couple of stars observed from Earth). Measurement Since the angular distance (or separation) is conceptually identical to an angle, it is measured in the same Units of measurement, units, such as Degree (angle), degrees or radians, using instruments such as goniometers or optical instruments specially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. Angles formed by two rays lie in the plane (geometry), plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection. ''Angle'' is also used to designate the measurement, measure of an angle or of a Rotation (mathematics), rotation. This measure is the ratio of the length of a arc (geometry), circular arc to its radius. In the case of a geometric angle, the arc is centered at the vertex and delimited by the sides. In the case of a rotation, the arc is centered at the center of the rotation and delimited by any other point and its image by the rotation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Units Of Measurement
A unit of measurement is a definite magnitude (mathematics), magnitude of a quantity, defined and adopted by convention or by law, that is used as a standard for measurement of the same kind of quantity. Any other quantity of that kind can be expressed as a multiple of the unit of measurement. For example, a length is a physical quantity. The metre (symbol m) is a unit of length that represents a definite predetermined length. For instance, when referencing "10 metres" (or 10 m), what is actually meant is 10 times the definite predetermined length called "metre". The definition, agreement, and practical use of units of measurement have played a crucial role in human endeavour from early ages up to the present. A multitude of System of measurement, systems of units used to be very common. Now there is a global standard, the International System of Units (SI), the modern form of the metric system. In trade, weights and measures is often a subject of governmental r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fig Angle Separation Planar
The fig is the edible fruit of ''Ficus carica'', a species of small tree in the flowering plant family Moraceae. Native to the Mediterranean and western Asia, it has been cultivated since ancient times and is now widely grown throughout the world, both for its fruit and as an ornamental plant.''The Fig: its History, Culture, and Curing'', Gustavus A. Eisen, Washington, Govt. print. off., 1901 ''Ficus carica'' is the type species of the genus ''Ficus'', containing over 800 tropical and subtropical plant species. A fig plant is a small deciduous tree or large shrub growing up to tall, with smooth white bark. Its large leaves have three to five deep lobes. Its fruit (referred to as syconium, a type of multiple fruit) is tear-shaped, long, with a green skin that may ripen toward purple or brown, and sweet soft reddish flesh containing numerous crunchy seeds. The milky sap of the green parts is an irritant to human skin. In the Northern Hemisphere, fresh figs are in season from lat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small-angle Approximation
The small-angle approximations can be used to approximate the values of the main trigonometric functions, provided that the angle in question is small and is measured in radians: : \begin \sin \theta &\approx \theta \\ \cos \theta &\approx 1 - \frac \approx 1\\ \tan \theta &\approx \theta \end These approximations have a wide range of uses in branches of physics and engineering, including mechanics, electromagnetism, optics, cartography, astronomy, and computer science. One reason for this is that they can greatly simplify differential equations that do not need to be answered with absolute precision. There are a number of ways to demonstrate the validity of the small-angle approximations. The most direct method is to truncate the Maclaurin series for each of the trigonometric functions. Depending on the order of the approximation, \textstyle \cos \theta is approximated as either 1 or as 1-\frac. Justifications Graphic The accuracy of the approximations can be seen belo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dot Product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more). Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. In mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
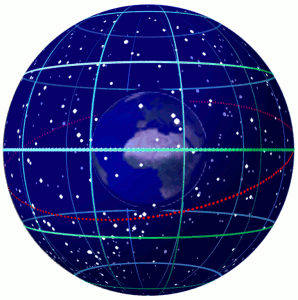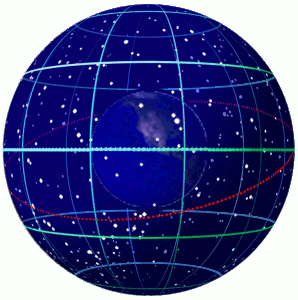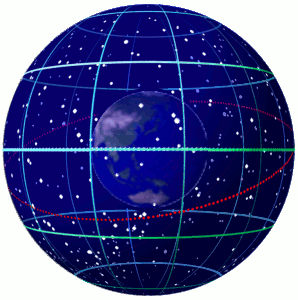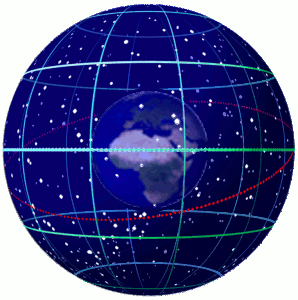
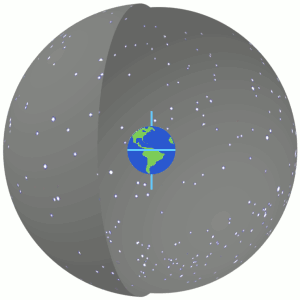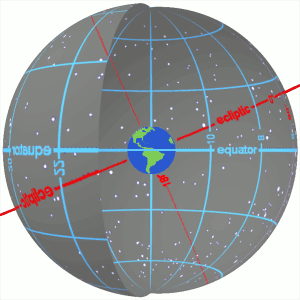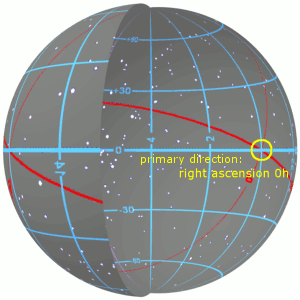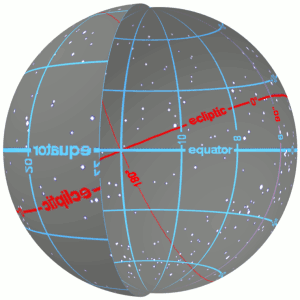
Celestial Sphere
In astronomy and navigation, the celestial sphere is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the celestial sphere, which may be centered on Earth or the observer. If centered on the observer, half of the sphere would resemble a hemispherical screen over the observing location. The celestial sphere is a conceptual tool used in spherical astronomy to specify the position of an object in the sky without consideration of its linear distance from the observer. The celestial equator divides the celestial sphere into northern and southern hemispheres. Introduction Because astronomical objects are at such remote distances, casual observation of the sky offers no information on their actual distances. All celestial objects seem equally far away, as if fixed onto the inside of a sphere with a large but unknown radius, which appears to rotate westward o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
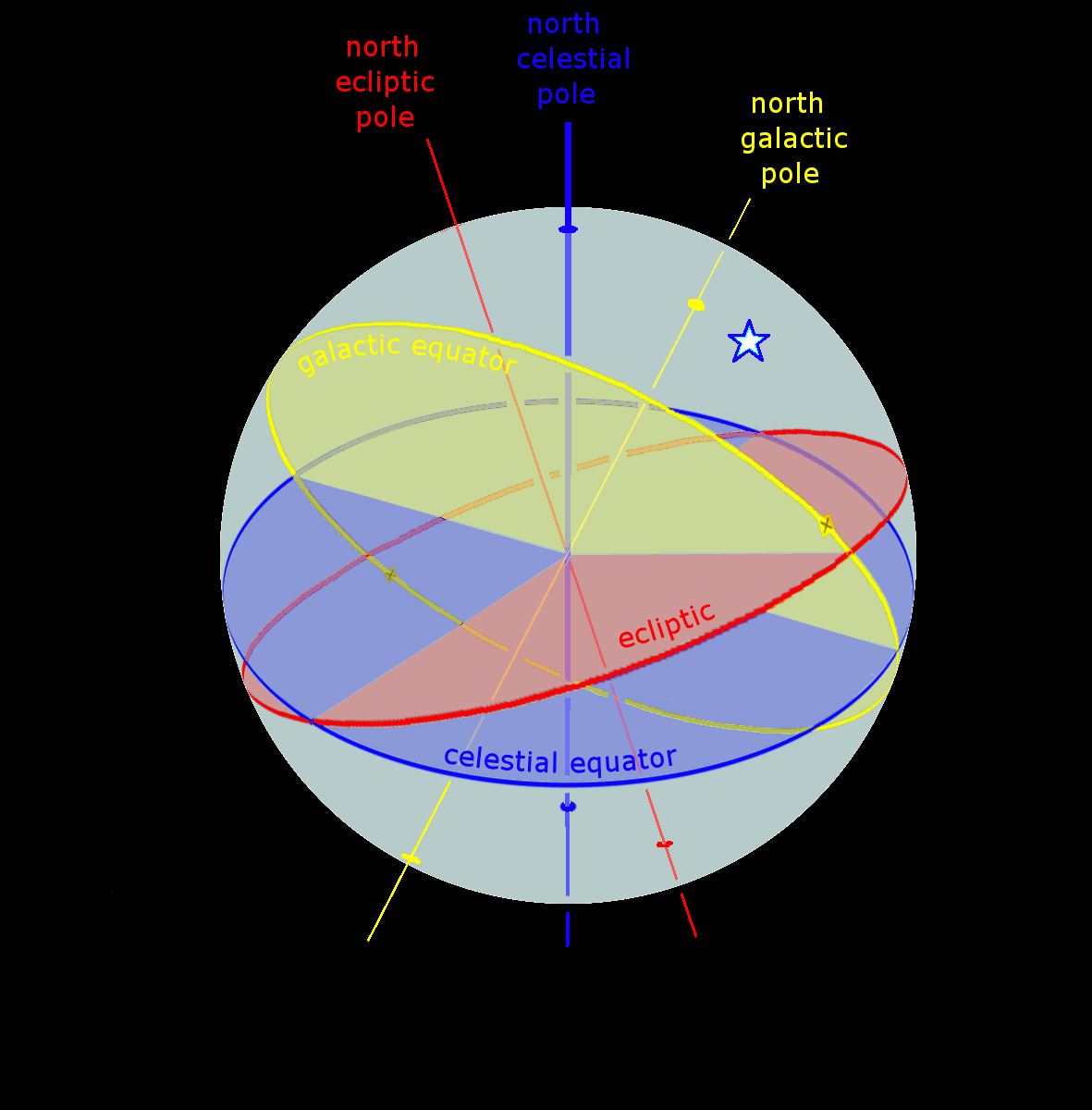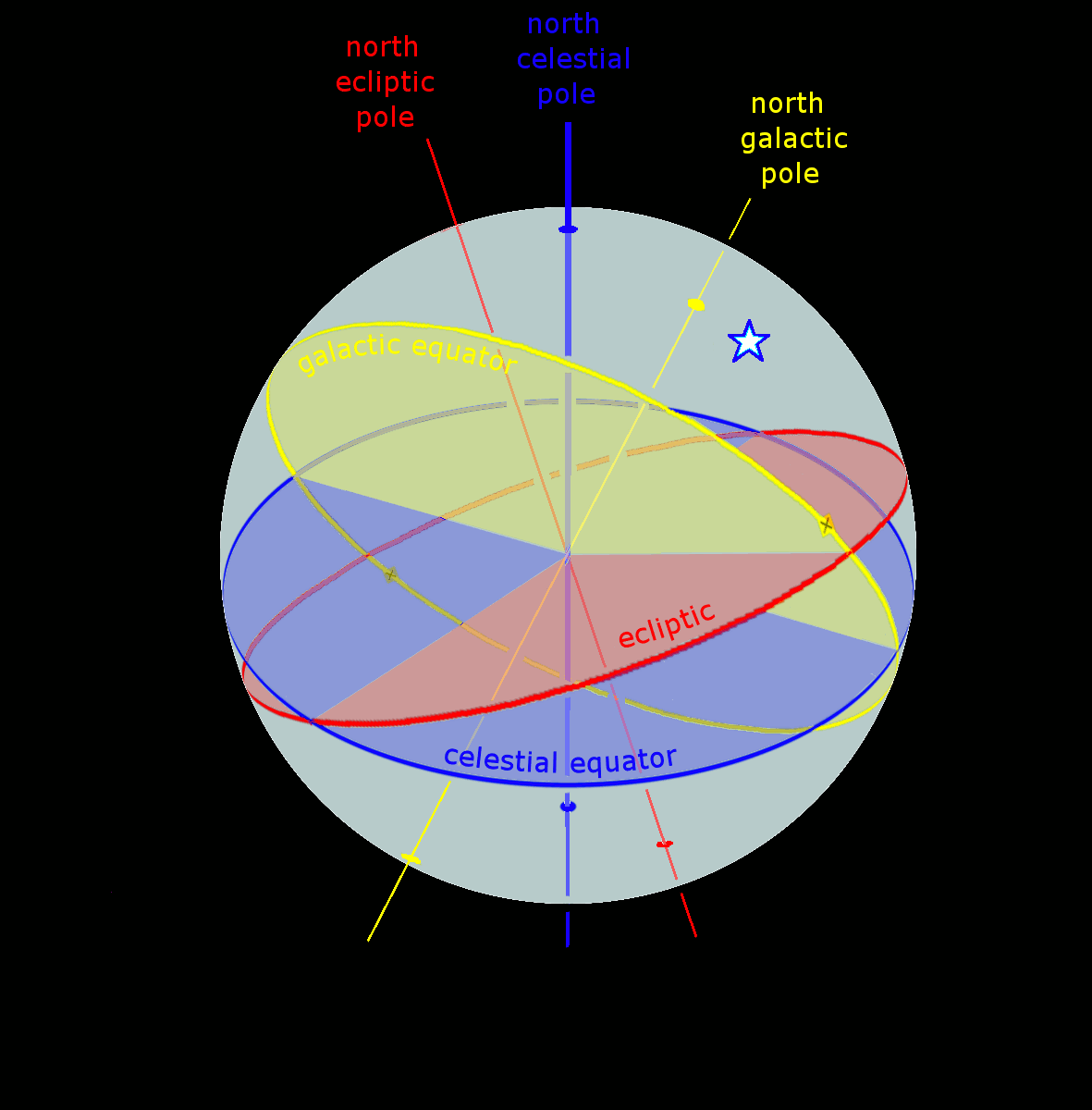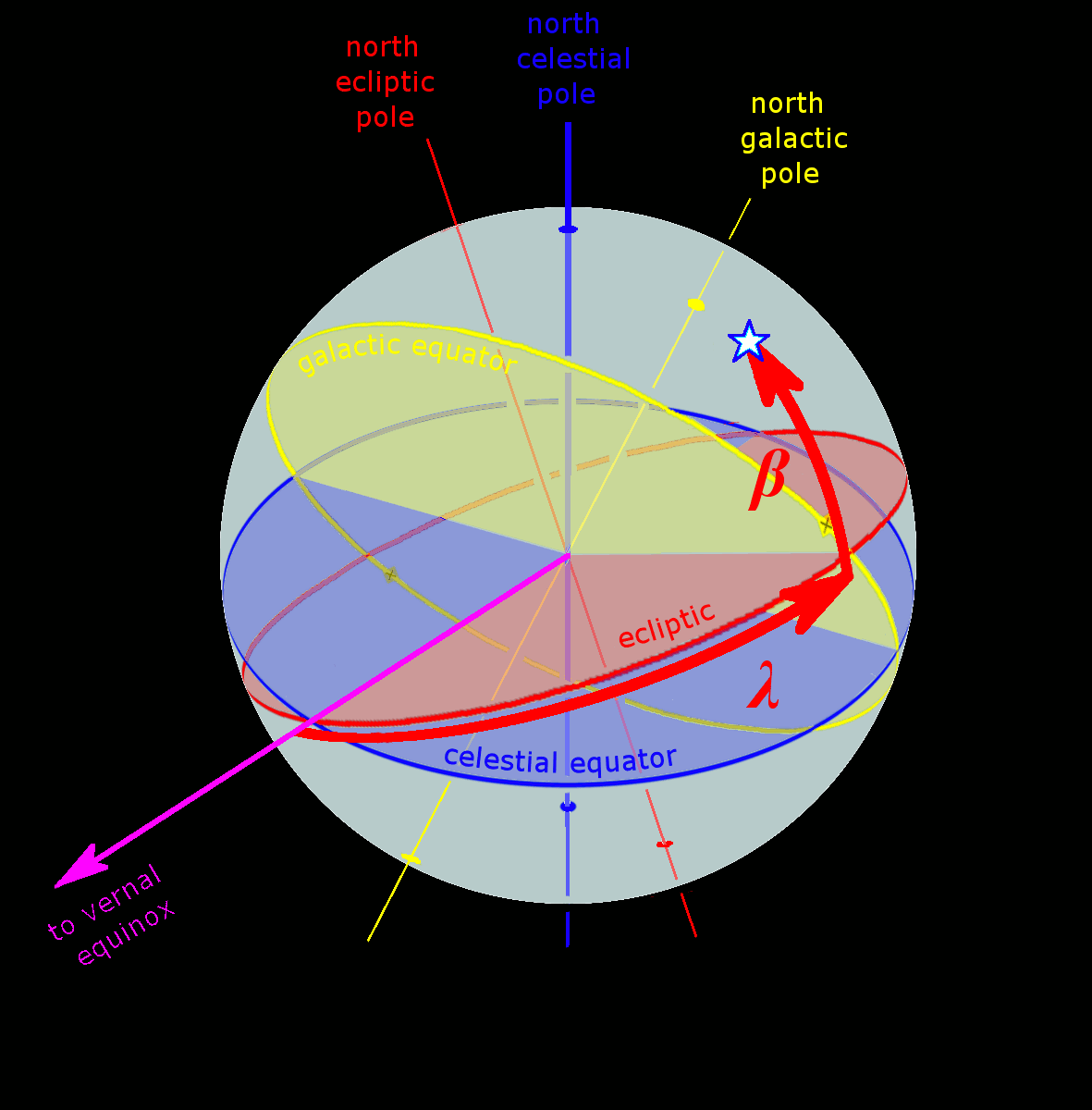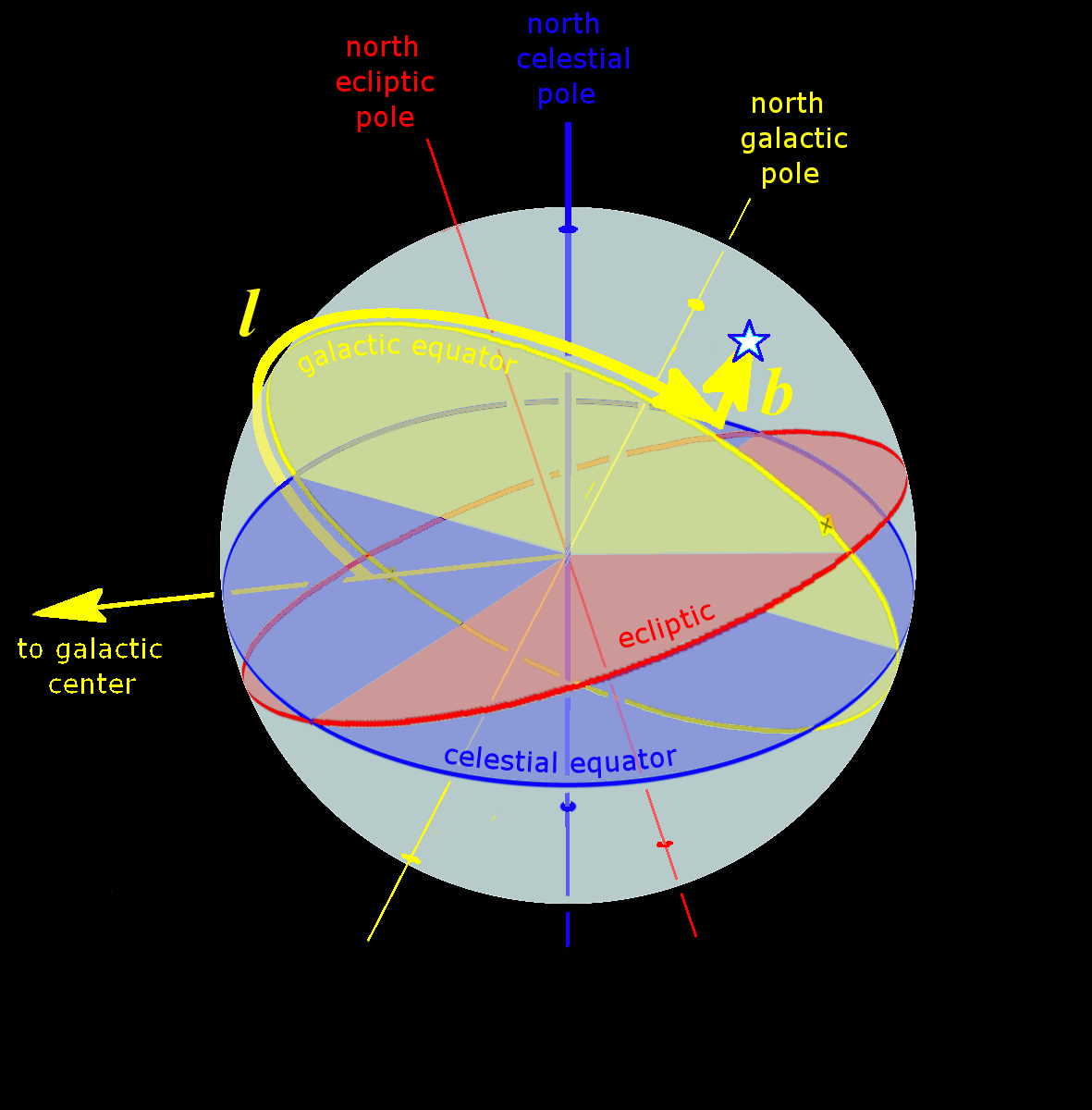
Declination
In astronomy, declination (abbreviated dec; symbol ''δ'') is one of the two angles that locate a point on the celestial sphere in the equatorial coordinate system, the other being hour angle. Declination's angle is measured north or south of the celestial equator, along the hour circle passing through the point in question. The root of the word ''declination'' (Latin, ''declinatio'') means "a bending away" or "a bending down". It comes from the same root as the words ''incline'' ("bend foward") and ''recline'' ("bend backward"). In some 18th and 19th century astronomical texts, declination is given as ''North Pole Distance'' (N.P.D.), which is equivalent to 90 – (declination). For instance an object marked as declination −5 would have an N.P.D. of 95, and a declination of −90 (the south celestial pole) would have an N.P.D. of 180. Explanation Declination in astronomy is comparable to geographic latitude, projected onto the celestial sphere, and right ascension is like ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Ascension
Right ascension (abbreviated RA; symbol ) is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the March equinox to the (hour circle of the) point in question above the earth. When paired with declination, these astronomical coordinates specify the location of a point on the celestial sphere in the equatorial coordinate system. An old term, ''right ascension'' ( la, ascensio recta), "''Ascensio recta'' Solis, stellæ, aut alterius cujusdam signi, est gradus æquatorus cum quo simul exoritur in sphæra recta"; roughly translated, "''Right ascension'' of the Sun, stars, or any other sign, is the degree of the equator that rises together in a right sphere" refers to the ''ascension'', or the point on the celestial equator that rises with any celestial object as seen from Earth's equator, where the celestial equator intersects the horizon at a right angle. It contrasts with ''oblique ascension'', the point on the celestial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Celestial Coordinate System
Astronomical coordinate systems are organized arrangements for specifying positions of satellites, planets, stars, galaxies, and other celestial objects relative to physical reference points available to a situated observer (e.g. the true horizon and north cardinal direction to an observer situated on the Earth's surface). Coordinate systems in astronomy can specify an object's position in three-dimensional space or plot merely its direction on a celestial sphere, if the object's distance is unknown or trivial. Spherical coordinates, projected on the celestial sphere, are analogous to the geographic coordinate system used on the surface of Earth. These differ in their choice of fundamental plane, which divides the celestial sphere into two equal hemispheres along a great circle. Rectangular coordinates, in appropriate units, have the same fundamental () plane and primary (-axis) direction, such as a rotation axis. Each coordinate system is named after its choice of fundamental ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomical Objects
An astronomical object, celestial object, stellar object or heavenly body is a naturally occurring physical entity, association, or structure that exists in the observable universe. In astronomy, the terms ''object'' and ''body'' are often used interchangeably. However, an astronomical body or celestial body is a single, tightly bound, contiguous entity, while an astronomical or celestial ''object'' is a complex, less cohesively bound structure, which may consist of multiple bodies or even other objects with substructures. Examples of astronomical objects include planetary systems, star clusters, nebulae, and galaxies, while asteroids, moons, planets, and stars are astronomical bodies. A comet may be identified as both body and object: It is a ''body'' when referring to the frozen nucleus of ice and dust, and an ''object'' when describing the entire comet with its diffuse coma and tail. History Astronomical objects such as stars, planets, nebulae, asteroids and comets have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fig Angle Separation
The fig is the edible fruit of ''Ficus carica'', a species of small tree in the flowering plant family Moraceae. Native to the Mediterranean and western Asia, it has been cultivated since ancient times and is now widely grown throughout the world, both for its fruit and as an ornamental plant.''The Fig: its History, Culture, and Curing'', Gustavus A. Eisen, Washington, Govt. print. off., 1901 ''Ficus carica'' is the type species of the genus ''Ficus'', containing over 800 tropical and subtropical plant species. A fig plant is a small deciduous tree or large shrub growing up to tall, with smooth white bark. Its large leaves have three to five deep lobes. Its fruit (referred to as syconium, a type of multiple fruit) is tear-shaped, long, with a green skin that may ripen toward purple or brown, and sweet soft reddish flesh containing numerous crunchy seeds. The milky sap of the green parts is an irritant to human skin. In the Northern Hemisphere, fresh figs are in season from lat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Telescope
A telescope is a device used to observe distant objects by their emission, absorption, or reflection of electromagnetic radiation. Originally meaning only an optical instrument using lenses, curved mirrors, or a combination of both to observe distant objects, the word ''telescope'' now refers to a wide range of instruments capable of detecting different regions of the electromagnetic spectrum, and in some cases other types of detectors. The first known practical telescopes were refracting telescopes with glass lenses and were invented in the Netherlands at the beginning of the 17th century. They were used for both terrestrial applications and astronomy. The reflecting telescope, which uses mirrors to collect and focus light, was invented within a few decades of the first refracting telescope. In the 20th century, many new types of telescopes were invented, including radio telescopes in the 1930s and infrared telescopes in the 1960s. Etymology The word ''telescope'' was coin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |