|
Apeirohedron
In geometry, a skew apeirohedron is an infinite skew polyhedron consisting of nonplanar Face (geometry), faces or nonplanar vertex figures, allowing the figure to extend indefinitely without folding round to form a Surface (topology)#Closed_surfaces, closed surface. Skew apeirohedra have also been called polyhedral sponges. Many are directly related to a convex uniform honeycomb, being the polygonal surface of a Honeycomb (geometry), honeycomb with some of the cell (geometry), cells removed. Characteristically, an infinite skew polyhedron divides 3-dimensional space into two halves. If one half is thought of as ''solid'' the figure is sometimes called a partial honeycomb. Regular skew apeirohedra According to Coxeter, in 1926 John Flinders Petrie generalized the concept of regular skew polygons (nonplanar polygons) to ''regular skew polyhedra'' (apeirohedra). Coxeter and Petrie found three of these that filled 3-space: There also exist chiral polytope, chiral skew apeiroh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutetrahedron
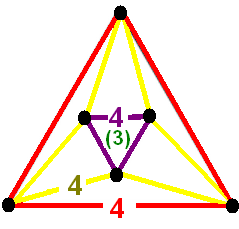
In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron, with either Skew polygon, skew regular Face (geometry), faces or skew regular vertex figures. History According to Coxeter, in 1926 John Flinders Petrie generalized the concept of regular skew polygons (nonplanar polygons) to finite regular skew polyhedron, regular skew polyhedra in 4-dimensions, and infinite regular skew apeirohedra in 3-dimensions (described here). Coxeter identified 3 forms, with planar faces and skew vertex figures, two are complements of each other. They are all named with a modified Schläfli symbol , where there are ''l''-gonal faces, ''m'' faces around each vertex, with ''holes'' identified as ''n''-gonal missing faces. Coxeter offered a modified Schläfli symbol for these figures, with implying the vertex figure, ''m'' l-gons around a vertex, and ''n''-gonal holes. Their vertex figures are skew polygons, zig-zagging between two planes. The regular skew polyhedra, represen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Muoctahedron
In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron, with either skew regular faces or skew regular vertex figures. History According to Coxeter, in 1926 John Flinders Petrie generalized the concept of regular skew polygons (nonplanar polygons) to finite regular skew polyhedra in 4-dimensions, and infinite regular skew apeirohedra in 3-dimensions (described here). Coxeter identified 3 forms, with planar faces and skew vertex figures, two are complements of each other. They are all named with a modified Schläfli symbol , where there are ''l''-gonal faces, ''m'' faces around each vertex, with ''holes'' identified as ''n''-gonal missing faces. Coxeter offered a modified Schläfli symbol for these figures, with implying the vertex figure, ''m'' l-gons around a vertex, and ''n''-gonal holes. Their vertex figures are skew polygons, zig-zagging between two planes. The regular skew polyhedra, represented by , follow this equation: * 2 sin(/''l'') · ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mucube
In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron, with either skew regular faces or skew regular vertex figures. History According to Coxeter, in 1926 John Flinders Petrie generalized the concept of regular skew polygons (nonplanar polygons) to finite regular skew polyhedra in 4-dimensions, and infinite regular skew apeirohedra in 3-dimensions (described here). Coxeter identified 3 forms, with planar faces and skew vertex figures, two are complements of each other. They are all named with a modified Schläfli symbol , where there are ''l''-gonal faces, ''m'' faces around each vertex, with ''holes'' identified as ''n''-gonal missing faces. Coxeter offered a modified Schläfli symbol for these figures, with implying the vertex figure, ''m'' l-gons around a vertex, and ''n''-gonal holes. Their vertex figures are skew polygons, zig-zagging between two planes. The regular skew polyhedra, represented by , follow this equation: * 2 sin(/''l'') · ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Space Group
In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc, and alternatively called ''cubic close-packed'' or ccp) Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive unit cells often are not. Bravais lattices The three Bravais lattices in the cubic crystal system are: The primitive cubic lattice (cP) consists of one lattice point on each corner of the cube; this means each simple cubic unit cell has in total one lattice point. Each atom at a lattice point is then shared equally between eight adjacent cubes, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schläfli Symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations. The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more than three dimensions and discovered all their convex regular polytopes, including the six that occur in four dimensions. Definition The Schläfli symbol is a recursive description, starting with for a ''p''-sided regular polygon that is convex. For example, is an equilateral triangle, is a square, a convex regular pentagon, etc. Regular star polygons are not convex, and their Schläfli symbols contain irreducible fractions ''p''/''q'', where ''p'' is the number of vertices, and ''q'' is their turning number. Equivalently, is created from the vertices of , connected every ''q''. For example, is a pentagram; is a pentagon. A regular polyhedron that has ''q'' regular ''p''-sided Face (geometry), polygon faces around each Verte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Melinda Green
The Buddhabrot is the probability distribution over the trajectories of points that escape the Mandelbrot fractal. Its name reflects its pareidolic resemblance to classical depictions of Gautama Buddha, seated in a meditation pose with a forehead mark ('' tikka''), a traditional topknot (''ushnisha'') and ringlet hair. Discovery The ''Buddhabrot'' rendering technique was discovered by Melinda Green, who later described it in a 1993 Usenet post to sci.fractals. Previous researchers had come very close to finding the precise Buddhabrot technique. In 1988, Linas Vepstas relayed similar images to Cliff Pickover for inclusion in Pickover's then-forthcoming book ''Computers, Pattern, Chaos, and Beauty''. This led directly to the discovery of Pickover stalks. Noel Griffin also implemented this idea in the 1993 "Mandelcloud" option in the Fractint renderer. However, these researchers did not filter out non-escaping trajectories required to produce the ghostly forms reminiscent of Hindu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbifold Notation
In geometry, orbifold notation (or orbifold signature) is a system, invented by the mathematician William Thurston and promoted by John Conway, for representing types of symmetry groups in two-dimensional spaces of constant curvature. The advantage of the notation is that it describes these groups in a way which indicates many of the groups' properties: in particular, it follows William Thurston in describing the orbifold obtained by taking the quotient of Euclidean space by the group under consideration. Groups representable in this notation include the point groups on the sphere (S^2), the frieze groups and wallpaper groups of the Euclidean plane (E^2), and their analogues on the hyperbolic plane (H^2). Definition of the notation The following types of Euclidean transformation can occur in a group described by orbifold notation: * reflection through a line (or plane) * translation by a vector * rotation of finite order around a point * infinite rotation around a line in 3- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Notation
In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson. Reflectional groups For Coxeter groups, defined by pure reflections, there is a direct correspondence between the bracket notation and Coxeter-Dynkin diagram. The numbers in the bracket notation represent the mirror reflection orders in the branches of the Coxeter diagram. It uses the same simplification, suppressing 2s between orthogonal mirrors. The Coxeter notation is simplified with exponents to represent the number of branches in a row for linear diagram. So the ''A''''n'' group is represented by ''n''−1 to imply ''n'' nodes connected by ''n−1'' order-3 branches. Exampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Face-transitive
In geometry, a tessellation of dimension (a plane tiling) or higher, or a polytope of dimension (a polyhedron) or higher, is isohedral or face-transitive if all its faces are the same. More specifically, all faces must be not merely congruent but must be ''transitive'', i.e. must lie within the same '' symmetry orbit''. In other words, for any two faces and , there must be a symmetry of the ''entire'' figure by translations, rotations, and/or reflections that maps onto . For this reason, convex isohedral polyhedra are the shapes that will make fair dice. Isohedral polyhedra are called isohedra. They can be described by their face configuration. An isohedron has an even number of faces. The dual of an isohedral polyhedron is vertex-transitive, i.e. isogonal. The Catalan solids, the bipyramids, and the trapezohedra are all isohedral. They are the duals of the (isogonal) Archimedean solids, prisms, and antiprisms, respectively. The Platonic solids, which are either self-du ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibrifold Notation
In mathematics, a fibrifold is (roughly) a fiber space whose fibers and base spaces are orbifolds. They were introduced by , who introduced a system of notation for 3-dimensional fibrifolds and used this to assign names to the 219 affine space group types. 184 of these are considered reducible, and 35 irreducible. Irreducible cubic space groups The 35 irreducible space groups correspond to the cubic space group. Irreducible group symbols (indexed 195−230) in Hermann–Mauguin notation, Fibrifold notation, geometric notation, and Coxeter notation In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram ...: References * * * * * Symmetry Finite groups Discrete groups {{geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices. The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron a 3-zonohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations. The cube is dual to the octahedron. It has cubical or octahedral symmetry. The cube is the only convex polyhedron whose faces are all squares. Orthogonal projections The ''cube'' has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes. Spherical tiling The cube can also be represented as a spherical tiling, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |